»нтервал
–ассмотренные точечные оценки параметров распределени€ дают оценку в виде числа, наиболее близкого к значению неизвестного параметра. “акие оценки используют только при большом числе измерений. „ем меньше объем выборки, тем легче допустить ошибку при выборе параметра. ƒл€ практики важно не только получить точечную оценку, но и определить интервал, называемый доверительным, между границами которого с заданной дове рителъной веро€тностью

где q Ч уровень значимости; хн, хвЧ нижн€€ и верхн€€ границы интервала, находитс€ истинное значение оцениваемого параметра.
¬ общем случае доверительные интервалы можно строить на основе неравенства „ебышева. ѕри любом законе распределени€ случайной величины, обладающей моментами первых двух пор€дков, верхн€€ граница веро€тности попадани€ отклонени€ случайной величины х от центра распределени€ ’ц в интервал tSx описываетс€ неравенством „ебышева

где Sx Ч оценка — ќ распределени€; t Ч положительное число.
ƒл€ нахождени€ доверительного интервала не требуетс€ знать закон распределени€ результатов наблюдений, но нужно знать оценку — ќ. ѕолученные с помощью неравенства „ебышева интервалы оказываютс€ слишком широкими дл€ практики. “ак, доверительной веро€тности 0,9 дл€ многих законов распределений соответствует доверительный интервал 1,6SX. Ќеравенство „ебышева дает в данном случае 3,16SX. ¬ св€зи с этим оно не получило широкого распространени€.
¬ метрологической практике используют главным образом кван-тильные оценки доверительного интервала. ѕод 100P-процентным квантилем хр понимают абсциссу такой вертикальной линии, слева от которой площадь под кривой плотности распределени€ равна –%. »наче говор€, квантиль Ч это значение случайной величины (погрешности) с заданной доверительной веро€тностью –. Ќапример, медиана распределени€ €вл€етс€ 50%-ным квантилем х0,5.
Ќа практике 25- и 75%-ный квантили прин€то называть сгибами, или квантил€ми распределени€. ћежду ними заключено 50% всех возможных значений случайной величины, а остальные 50% лежат вне их. »нтервал значений случайной величины х между х0 05 и х0 95 охватывает 90% всех ее возможных значений и называетс€ интерквантильным промежутком с 90%-ной веро€тностью. ≈го прот€женность равна d0,9= х0,95 - х0,05.
Ќа основании такого подхода вводитс€ пон€тие квантильных значений погрешности, т.е. значений погрешности с заданной доверительной веро€тностью – Ч границ интервала неопределенности ± Dƒ = ± (хр - х1-р)/2 = ± dp/2. Ќа его прот€женности встречаетс€ –% значений случайной величины (погрешности), a q = (1- –)% общего их числа остаютс€ за пределами этого интервала.
ƒл€ получени€ интервальной оценки нормально распределенной случайной величины необходимо:
Х определить точечную оценку ћќ х̅ и — ќ Sx случайной величины по формулам (6.8) и (6.11) соответственно;
Х выбрать доверительную веро€тность – из рекомендуемого р€да значений 0,90; 0,95; 0,99;
Х найти верхнюю хв и нижнюю хн границы в соответствии с уравнени€ми

полученными с учетом (6.1). «начени€ хн и хв определ€ютс€ из таблиц значений интегральной функции распределени€ F(t) или функции Ћапласа ‘(1).
|
|
|
ѕолученный доверительный интервал удовлетвор€ет условию
 (6.13)
(6.13)
где n Ч число измеренных значений; zp Ч аргумент функции Ћапласа ‘(1), отвечающей веро€тности –/2. ¬ данном случае zp называетс€ квантильным множителем. ѕоловина длины доверительного интервала  называетс€ доверительной границей погрешности результата измерений.
называетс€ доверительной границей погрешности результата измерений.
ѕример 6.1. ѕроизведено 50 измерений посто€нного сопротивлени€. ќпределить доверительный интервал дл€ ћќ значени€ посто€нного сопротивлени€, если закон распределени€ нормальный с параметрами mx = R = 590 ќм, Sx= 90 ќм при доверительной веро€тности – = 0,9.
“ак как гипотеза о нормальности закона распределени€ не противоречит опытным данным, доверительный интервал определ€етс€ по формуле

ќтсюда ‘(zр) = 0,45. »з таблицы, приведенной в приложении 1, находим, что zp= 1,65. —ледовательно, доверительный интервал запишетс€ в виде
 или 590 - 21 < R < 590 + 21. ќкончательно 509 ќм < R < 611 ќм.
или 590 - 21 < R < 590 + 21. ќкончательно 509 ќм < R < 611 ќм.
ѕри отличии закона распределени€ случайной величины от нормального необходимо построить его математическую модель и определ€ть доверительный интервал с ее использованием.
–ассмотренный способ нахождени€ доверительных интервалов справедлив дл€ достаточно большого числа наблюдений n, когда s = Sx. —ледует помнить, что вычисл€ема€ оценка — ќ Sx €вл€етс€ лишь некоторым приближением к истинному значению s. ќпределение доверительного интервала при заданной веро€тности оказываетс€ тем менее надежным, чем меньше число наблюдений. Ќельз€ пользоватьс€ формулами нормального распределени€ при малом числе наблюдений, если нет возможности теоретически на основе предварительных опытов с достаточно большим числом наблюдений определить — ќ.
–асчет доверительных интервалов дл€ случа€, когда распределение результатов наблюдений нормально, но их дисперси€ неизвестна, т.е. при малом числе наблюдений п, возможно выполнить с использованием распределени€ —тьюдента S(t,k). ќно описывает плотность распределени€ отношени€ (дроби —тьюдента):

где Q Ч истинное значение измер€емой величины. ¬еличины х̅, Sx. и Sx̅ вычисл€ютс€ на основании опытных данных и представл€ют собой точечные оценки ћќ, — ќ результатов измерений и — ќ среднего арифметического значени€.
¬еро€тность того, что дробь —тьюдента в результате выполненных наблюдений примет некоторое значение в интервале (- tp; + tp)

(6.14)
где k Ч число степеней свободы, равное (п - 1). ¬еличины tp (называемые в данном случае коэффициентами —тьюдента), рассчитанные с помощью двух последних формул дл€ различных значений доверительной веро€тности и числа измерений, табулированы (см. таблицу в приложении 1). —ледовательно, с помощью распределени€ —тьюдента можно найти веро€тность того, что отклонение среднего арифметического от истинного значени€ измер€емой величины не превышает 
¬ тех случа€х, когда распределение случайных погрешностей не €вл€етс€ нормальным, все же часто пользуютс€ распределением —тьюдента с приближением, степень которого остаетс€ неизвестной. –аспределение —тьюдента примен€ют при числе измерений n < 30, поскольку уже при n = 20,...,30 оно переходит в нормальное и вместо уравнени€ (6.14) можно использовать уравнение (6.13). –езультат измерени€ записываетс€ в виде: 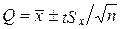 ; P = –д, где –д Ч конкретное значение доверительной веро€тности. ћножитель t при большом числе измерений n равен квантильному множителю zp. ѕри малом n он равен коэффициенту —тьюдента.
; P = –д, где –д Ч конкретное значение доверительной веро€тности. ћножитель t при большом числе измерений n равен квантильному множителю zp. ѕри малом n он равен коэффициенту —тьюдента.
|
|
|
ѕолученный результат измерени€ не €вл€етс€ одним конкретным числом, а представл€ет собой интервал, внутри которого с некоторой веро€тностью –д находитс€ истинное значение измер€емой величины. ¬ыделение середины интервала х вовсе не предполагает, что истинное значение ближе к нему, чем к остальным точкам интервала. ќно может быть в любом месте интервала, а с веро€тностью 1 - –д даже вне его.
ѕример 6.2. ќпределение удельных магнитных потерь дл€ различных образцов одной партии электротехнической стали марки 2212 дало следующие результаты: 1,21; 1,17; 1,18; 1,13; 1,19; 1,14; 1,20 и 1,18 ¬т/кг. —чита€, что систематическа€ погрешность отсутствует, а случайна€ распределена по нормальному закону, требуетс€ определить доверительный интервал при значени€х доверительной веро€тности 0,9 и 0,95. ƒл€ решени€ задачи использовать формулу Ћапласа и распределение —тьюдента.
ѕо формулам (6.8) в (6.11) находим оценки среднего арифметического значени€ и — ќ результатов измерений. ќни соответственно равны 1,18 и 0,0278 ¬т/кг. —чита€, что оценка — ќ равна самому отклонению, находим:

ќтсюда, использу€ значени€ функции Ћапласа, приведенные в таблице приложени€ 1, определ€ем, что zp = 1,65. ƒл€ – = 0,95 коэффициент zp =1,96. ƒоверительные интервалы, соответствующие – = 0,9 и 0,95, равны 1,18 ± 0,016 и 1,18±0,019 ¬т/кг.
¬ том случае, когда нет оснований считать, что — ќ и его оценка равны, доверительный интервал определ€етс€ на основе распределени€ —тьюдента:

ѕо таблице приложени€ 1 находим, что t0,9 = 1,9 и t0,95 = 2,37. ќтсюда доверительные интервалы соответственно равны 1,18±0,019 и 1,18±0,023 ¬т/кг.
онтрольные вопросы.
1.ѕри каких услови€х погрешность измерени€ может рассматриватьс€ как случайна€ величина?
2. ѕеречислите свойства интегральной и дифференциальной функций распределени€ случайной величины.
3. Ќазовите числовые параметры законов распределени€.
4. аким образом может задаватьс€ центр распределени€?
5. „то такое моменты распределени€? акие из них нашли применение в метрологии?
6. Ќазовите основные классы распределений, используемых в метрологии.
7. ƒайте характеристику распределени€м, вход€щим в класс трапецеидальных распределений.
8. „то такое экспоненциальные распределени€? аковы их свойства и характеристики?
9. „то такое нормальное распределение? ѕочему оно играет особую роль в метрологии?
10. „то такое функци€ Ћапласа и дл€ чего она используетс€?
11. ак описываетс€ и где используетс€ семейство распределений —тьюдента?
12. акие точечные оценки законов распределени€ вы знаете? акие требовани€ предъ€вл€ютс€ к ним?
13. „то такое доверительный интервал? акие "способы его задани€ вам известны?






