Продукт реализуется на рынке несовершенной конкуренции. Заданы функции спроса на продукцию фирмы и предложения ресурсов. Функция спроса имеет однородную форму  , где
, где  ,
,  - цена продукта,
- цена продукта,  - ценовая эластичность спроса. Если
- ценовая эластичность спроса. Если 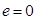 , то цена продукта станет постоянной величиной и получим условия совершенной конкуренции. Обратная функция спроса
, то цена продукта станет постоянной величиной и получим условия совершенной конкуренции. Обратная функция спроса  , где
, где 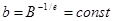 . Валовой доход фирмы
. Валовой доход фирмы  . Если
. Если  , то валовой доход является постоянным, не зависящим от изменения или цены
, то валовой доход является постоянным, не зависящим от изменения или цены  или объема выпуска
или объема выпуска  . Это значит, что объем производства является заданной величиной
. Это значит, что объем производства является заданной величиной  , а, следовательно, и цена
, а, следовательно, и цена  в выражении (
в выражении ( ) также постоянна.
) также постоянна.
Функции предложения труда 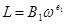 , капитала
, капитала  также однородны,
также однородны, 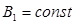 и
и  ,
,  и
и  - эластичности предложения факторов производства,
- эластичности предложения факторов производства,  и
и  , соответственно, ставка заработной платы и процент на единицу капитала.
, соответственно, ставка заработной платы и процент на единицу капитала.
Определим  и
и  как обратные функции предложения труда и капитала при названных условиях. Тогда
как обратные функции предложения труда и капитала при названных условиях. Тогда  , где
, где  . Затраты труда и капитала равны соответственно:
. Затраты труда и капитала равны соответственно:  .
.
Запишем функцию Лагранжа для экономической прибыли:
 , где
, где  - множитель Лагранжа.
- множитель Лагранжа.
Необходимые условия максимизации прибыли:
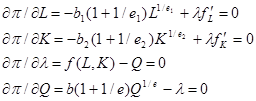
Последнее уравнение добавляется, если 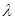 является переменной величиной. Из системы уравнений находим:
является переменной величиной. Из системы уравнений находим:

Если  , то
, то  .
.
Если  , то
, то 
Определим факторные цены в условиях несовершенной конкуренции:
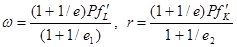
Полученные выражения отражают характер зависимости заработной платы и ставки процента от рыночных параметров – цены товара, ценовой эластичности спроса на товар, ценовой эластичности предложения труда и капитала, а также предельной производительности труда и капитала. Решая систему уравнений, представляющую необходимое условие максимизации прибыли, находим значения  ,
,  ,
, 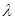 и
и  .
.
Достаточное условие максимизации прибыли  <0. Если оно выполняется при найденных значениях
<0. Если оно выполняется при найденных значениях  ,
,  ,
, 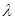 и
и  , то фирма получает максимальную прибыль.
, то фирма получает максимальную прибыль.
Концепция выявленной максимизации прибыли,
Ее практическое значение
Поскольку фирма максимизирует прибыль, ее величина должна быть не ниже того уровня, который сложился бы, если бы она по тем же ценам приобрела другое количество ресурсов и произвела другое количество продукции. Это правило известно как слабая аксиома минимизации прибыли. При ее выполнении должны выполняться следующие неравенства:
 , (3.5)
, (3.5)
 , (3.6)
, (3.6)
где  ,
,  и
и  – оптимальные количества выпуска, капитала и труда при ценах
– оптимальные количества выпуска, капитала и труда при ценах 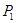 ,
,  и
и  ;
; 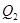 ,
,  и
и 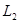 - оптимальные количества выпуска, капитала и труда при ценах
- оптимальные количества выпуска, капитала и труда при ценах  ,
,  и
и  .
.
Поменяем местами стороны неравенства (3.6):
 .
.
Прибавим полученное выражение к неравенству (2.5), получим:
 .
.
Вынесем за скобки подобные члены:
 .
.
Вновь вынесем за скобки подобные члены и перенесем все слагаемые в левую часть:
 . (3.7)
. (3.7)
Выражения в скобках неравенства (3.7) характеризуют: изменения цен на готовую продукцию 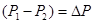 , объемов выпуска
, объемов выпуска  , цен на капитальные ресурсы
, цен на капитальные ресурсы 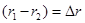 , количества капитала
, количества капитала  , цен на труд
, цен на труд  , и количества труда
, и количества труда  . Неравенство (3.7) трансформируется в неравенство (3.8):
. Неравенство (3.7) трансформируется в неравенство (3.8):
 . (3.8)
. (3.8)
Слабая аксиома максимизации прибыли предполагает соблюдение неравенства (3.8). Если при прежней технологии производства фирма в ответ на изменения цен выпускаемой продукции или ресурсов изменяет выпуск и количества потребляемых ресурсов, то, подставляя значения соответствующих изменений в неравенство (3.8), можно дать первичную оценку деятельности фирмы. Если неравенство не соблюдается, значит, либо до изменения цен, либо после изменения, либо и до, и после изменения цен фирма не максимизировала прибыль.






