Производство с двумя переменными факторами
Заданный объем производства можно произвести при различном сочетании затрачиваемых ресурсов. Среди них находится сочетание, обеспечивающее минимум затрат. При выполнении правила наименьших издержек 
каждый рубль, затрачиваемый на любой ресурс, позволяет фирме получить одинаковый предельный продукт.
Чтобы прибыль фирмы была максимальной, недостаточно минимизировать издержки. Существует несколько объемов производства, при которых продукт можно производить с минимальными затратами, и только один объем выпуска, при котором прибыль максимальна.
Существует строгое математическое обоснование необходимых и достаточных условий получения максимальной прибыли фирмой. В теоретическом анализе используем классические методы определения экстремума затрат и прибыли. В условиях чистой конкуренции фирма покупает факторы производства по ценам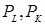 
и продает продукт по цене 
. Определим такую комбинацию затрат труда и капитала, при которой прибыль фирмы максимальна.
На основе определения экономической прибыли запишем ее функцию:
. (3.1)
Необходимым условием максимума прибыли - функции двух переменных - является равенство нулю первых частных производных: 
, или
(3.2)
Решим систему уравнений (3.2) и определим расходуемые количества труда и капитала как функции факторных цен и цены продукта, тем самым определим, как говорят математики, критические точки. Условие (3.2) можно представить в форме 
. Оно означает, что для достижения максимума прибыли необходимо, чтобы предельная норма технологического замещения (левая часть равенства) была равна соотношению цен факторов производства. При выполнении такого условия фирма обеспечит минимальные издержки на выпуск. Необходимое условие максимизации прибыли позволяет определить не одно, а несколько сочетаний затрат труда и капитала, обеспечивающих минимальные издержки при различных выпусках. В этом заключается экономическое содержание необходимого условия максимизации прибыли фирмой.
Выделим из всех найденных критических точек 
сочетание труда и капитала 
, которое обеспечит максимум прибыли и отвечает достаточному условию максимума прибыли. Из математического анализа известно, что надо исследовать, остается ли неизменным знак разности [ 
] для всех точек, достаточно близких к каждой критической точке. Если разность сохраняет положительный знак, то в точке имеем минимум, если отрицательный - то максимум прибыли. Если разность не сохраняет знака, то в критической точке нет экстремума.
Исследование иногда облегчается применением другого достаточного условия, суть которого состоит в следующем. Полный дифференциал функции прибыли 
равен нулю в критических точках, так как в этих точках выполняется необходимое условие экстремума функции прибыли (2.2). Запишем второй дифференциал функции прибыли 
и введем обозначения: 
. Величины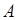 
и 
- вторые частные производные производственной функции по труду и капиталу измеряют наклоны кривых предельной производительности труда и предельной производительности капитала, имеют в любой заданной точке одинаковые знаки. Если предельная производительность труда и капитала убывает, то 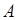и - отрицательные числа. Функция прибыли имеет в критической точке экстремум, если 
и не имеет экстремума, если 
. Вопрос об экстремуме остается открытым, если 
.
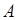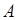Прибыль фирмы максимальна, если или отрицательна, прибыль минимальна, если или положительна. В критической точке выполняется достаточное условие максимума прибыли, и для затрат (
) определяем объем выпуска. Отсюда следует вывод: достаточное условие максимизации прибыли позволяет из всех возможных сочетаний затрат труда и капитала, обеспечивающих минимум затрат на производство продукции, выделить одно сочетание, позволяющее произвести такой объем продукции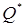 
и при заданной рынком цене продукта получить максимум прибыли.
Достаточным условием максимума функции прибыли является отрицательное значение дифференциала второго порядка 
при любых приращениях труда 
и капитала 
, не обращающихся в нуль одновременно. Если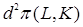 
принимает в зависимости от знака и dK положительные и отрицательные значения, то в критической точке экстремума функции прибыли нет. Если 
, то вопрос об экстремуме остается открытым.
Существует другой метод исследования условий, в которых фирма при минимальных издержках получает максимум прибыли. Это метод множителей Лагранжа, с помощью которого находят условный экстремум. Метод носит имя французского математика Ж.Л. Лагранжа (1736-1813). Используя такой метод, построим вспомогательную функцию Лагранжа для чистой прибыли:
. (3.3)
Она отличается от функции (3.1) слагаемым 
, где 
- множитель Лагранжа. Если фирма производит максимум продукции в соответствии с определением производственной функции, то выражение в квадратных скобках равно нулю и функция Лагранжа ведет себя точно так же, как и функция прибыли.
В действительности же нередко фирма в соответствии с изменяющейся конъюнктурой рынка производит различные объемы производства, отличающиеся от максимального возможного, и при таких объемах максимизирует прибыль. Данное обстоятельство учитывается названным выше слагаемым, максимум прибыли фирма получает при условии выпуска продукции в соответствии с технологической взаимосвязью выпуска и затрат в производственной функции.
