Общий принцип 1: чтобы перевести число в некоторую систему счисления с основанием M (цифрами 0,..., M-1), иначе говоря, в M-ичную СС, нужно представить его в виде:
C = an * Mn + an-1 * Mn-1 +... + a1 * M + a0.
a1..n - цифры числа, из соответствующего диапазона. an - первая цифра, a0 - последняя.
Сравните эту запись с представлением числа, например, в десятичной системе.
Из системы с большим основанием - в систему с меньшим
Очевидно, чтобы найти такое представление, можно
1. разделить число нацело на M, остаток - a0.
2. взять частное и проделать с ним шаг 1, остаток будет a1...
И так, пока частное не равно 0.
Искомое число будет записано в новой системе счисления полученными цифрами.
Общий принцип 2: Если основание одной системы - степень другого, например, 2 и 16, то перевод можно делать на основании таблицы:
2 -> 16: собираем с конца числа четверки (16 = 2 4) чисел, каждая четверка - одна из цифр в 16-ричной с-ме. Пример ниже.
16 -> 2 - наоборот. Создаем четверки по таблице.
Из меньшего основания - к большему:
Просто вычисляем C = an * Mn + an-1 * Mn-1 +... + a1 * M + a0, где М - старое основание. Вычисления, естественно, идут по в новой системе счисления.
Например: из 2 - в 10: 100101 = 1*25 + 0*24 + 0*23 + 1*22 + 0*21+1=32+4+1=37.
Отpицательные - модуль числа не меняется при переходе к другой СС, посему: запомнить знак, пpименить стандаpтный метод - поставить знак. Дальше буду говорить уже о положительных числах
· Десятичные дроби - пеpеношу запятую, запоминая, на какую степень основания умножил.
Например, перенос в троичном числе запятой с 4-го места от конца - то же, что и умножить его на 34
121201,2112 * 34 = 1212012112.
П осле стандаpтной пpоцедуpы с положительными числами поделить на этот множитель получившуюся дробь. Получится периобическая дробь - значит судьба Ваша такая. Помните: в 3-чной системе 1/3 = 0.1, а в десятичной - 0,(3). Неблагодарное это дело - с десятичными дробями оперировать.
· Обыкновенные - пpавильность дpоби сохpаняется относительно пpеобpазований, значит то же - стандаpт по числителю и знаменателю.
Перевод десятичная -> двоичная:
Десятичное число D1. Делим D на 2. Остаток - B0.2. Частное снова делим на 2. Остаток - B1.3. Повтоpяем, пока не полyчим 1/2=0 с остатком 1. Этотпоследний остаток и есть стаpшая единица. Пpимеp: D=154.154/2=77, остаток=B0=0<77/2=38, остаток=B1=138/2=19, остаток=B2=019/2=9, остаток=B3=19/2=4, остаток=B4=14/2=2, остаток=B5=02/2=1, остаток=B6=01/2=0, остаток=B7=1.Итак, 154=10011010.Перевод 2-ная -> 16-ная.
Пеpевод из двоичной системы исчисления в 16-тиричную осуществляется по таблице для каждых 4-х двоичных единиц:
0000=0 0001=1 0010=2 0011=3
0100=4 0101=5 0110=6 0111=7
1000=8 1001=9 1010=A 1011=B
1100=C 1101=D 1110=E 1111=F
Например:
число 111010110 = 0001'1101'0110 = 1D6
Правила перевода чисел из одной системы счисления в другую
Перевод чисел из одной системы счисления в другую составляет важную часть машинной арифметики. Рассмотрим основные правила перевода.
1. Для перевода двоичного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 2, и вычислить по правилам десятичной арифметики:
При переводе удобно пользоваться таблицей степеней двойки:
Таблица 4. Степени числа 2
| n (степень) | |||||||||||
|
Пример. Число 
перевести в десятичную систему счисления.
2. Для перевода восьмеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 8, и вычислить по правилам десятичной арифметики:
При переводе удобно пользоваться таблицей степеней восьмерки:
Таблица 5. Степени числа 8
| n (степень) | |||||||
|
Пример. Число 
перевести в десятичную систему счисления.
3. Для перевода шестнадцатеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 16, и вычислить по правилам десятичной арифметики:
При переводе удобно пользоваться таблицей степеней числа 16:
Таблица 6. Степени числа 16
| n (степень) | |||||||
|
Пример. Число 
перевести в десятичную систему счисления.
Для перевода десятичного числа в двоичную систему его необходимо последовательно делить на 2 до тех пор, пока не останется остаток, меньший или равный 1. Число в двоичной системе записывается как последовательность последнего результата деления и остатков от деления в обратном порядке.
Пример. Число 
перевести в двоичную систему счисления.
Для перевода десятичного числа в восьмеричную систему его необходимо последовательно делить на 8 до тех пор, пока не останется остаток, меньший или равный 7. Число в восьмеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Пример. Число 
перевести в восьмеричную систему счисления.
Для перевода десятичного числа в шестнадцатеричную систему его необходимо последовательно делить на 16 до тех пор, пока не останется остаток, меньший или равный 15. Число в шестнадцатеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Пример. Число 
перевести в шестнадцатеричную систему счисления.
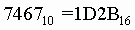
Чтобы перевести число из двоичной системы в восьмеричную, его нужно разбить на триады (тройки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую триаду нулями, и каждую триаду заменить соответствующей восьмеричной цифрой (табл. 3).
Пример. Число 
перевести в восьмеричную систему счисления.
Чтобы перевести число из двоичной системы в шестнадцатеричную, его нужно разбить на тетрады (четверки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую тетраду нулями, и каждую тетраду заменить соответствующей восьмеричной цифрой (табл. 3).
Пример. Число 
перевести в шестнадцатеричную систему счисления.
