Системы счисления и перевод чисел
Система счисления – это способ представления любого числа с помощью определенного набора символов, называемых цифрами. Основание системы счисления – это количество цифр, используемых в данной системе счисления.
Позиционными называются системы счисления, в которых значение цифры зависит от ее места (позиции) в записи числа. Непозиционными называются системы счисления, в которых значение цифры не зависит от ее места (позиции) в записи числа.
Позиционной является привычная для нас в повседневной жизни десятичная система счисления, в которой значение (вес) цифры зависит от ее позиции в записи числа. В числе 1111 одна и та же цифра 1 означает последовательно единицу, десяток, сотню, тысячу.
Все системы счисления, используемые в информатике (двоичная, восьмеричная, шестнадцатеричная и т. д.), являются позиционными. Это важно, т. к. правила образования чисел, перевода из одной системы в другую, выполнения арифметических операций во всех позиционных системах аналогичны.
Непозиционной системой счисления является, например, римская. Правила выполнения арифметических операций в непозиционных системах счисления совсем иные.
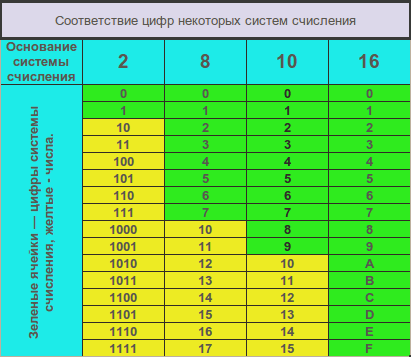
В 2-ной системе основание равно 2, т.е. используется всего 2 цифры - 0 и 1. В 8-ной основание равно 8, используются цифры от 0 до 7. В 16-ной системе основание равно 16, используются цифры от 0 до 15. Использование цифр 10, 11, 12, 13, 14, 15 в записи чисел неудобно, т. к. трудно отличить, например, цифру 12 от двух цифр – 1 и 2. Поэтому условились цифры от 10 до 15 обозначать латинскими буквами в порядке алфавита A, B, C, D, E, F.
Таблица соответствия цифр в различных системах счисления
Перевод целого числа из 10-ной системы счисления в любую другую
Посмотрите обучающее видео или прочитайте правило перевода в виде текста ниже.
Чтобы перевести целое число Х из 10-ной системы в любую другую с основанием Q:
1. делим Х на Q, в результате чего получается целая часть частного и остаток (может быть равен нулю, если разделилось нацело).
2. если полученная целая часть частного меньше Q, переходим к шагу 3. Если равно или больше Q, снова делим целую часть частного на Q, как описано в шаге 1. Внимание: делится только целая часть, остаток в делении не участвует (он пригодится позже).
3. все полученные остатки и последняя целая часть частного (меньшая, чем Q) преобразуются в соответствии с таблицей перевода в цифры той системы счисления, в которую выполняется перевод. Иными словами, если, к примеру, при переводе в 16-ную систему у вас получился остаток 12, то его нужно преобразовать в 16-ную цифру С.
4. Получаем ответ. Его первая (старшая) цифра - последнее частное, а остальные - остатки от деления, записанные в порядке, обратном порядку их получения.
Пример 1:

Пример 2:

Пример 3:







