Деление в двоичной системе счисления

Мы уже рассмотрели три действия и думаю уже понятно, что в общем-то действия над двоичными числами мало отличаются от действий над десятичными числами. Разница появляется только в том, что цифр две а не десять, но это только упрощает арифметические операции. Так же обстоит дело и с делением, но для лучшего понимания алгоритм деления разберём более подробно. Пусть нам необходимо разделить два десятичных числа, например 234 разделить на 7. Как мы это делаем.

Мы выделяем справа (от старшего разряда) такое количество цифр, чтобы получившееся число было как можно меньше и в то же время больше делителя. 2 - меньше делителя, следовательно, необходимое нам число 23. Затем делим полученное число на делитель с остатком. Получаем следующий результат:

-

Описанную операцию повторяем до тех пор, пока полученный остаток не окажется меньше делителя. Когда это случится, число полученное под чертой, это частное, а последний остаток - это остаток операции. Так вот операция деления двоичного числа выполняется точно также. Попробуем

Пример: 10010111 / 101

Ищем число, от старшего разряда которое первое было бы больше чем делитель. Это четырехразрядное число 1001. Оно выделено жирным шрифтом. Теперь необходимо подобрать делитель выделенному числу. И здесь мы опять выигрываем в сравнении в десятичной системой. Дело в том, что подбираемый делитель это обязательно цифра, а цифры у нас только две. Так как 1001 явно больше 101, то с делителем всё понятно это 1.

-

Итак, остаток от выполненной операции 100. Это меньше чем 101, поэтому чтобы выполнить второй шаг деления, необходимо добавить к 100 следующую цифру, это цифра 0. Теперь имеем следующее число:

-
-
	-

1000 больше 101 поэтому на втором шаге мы опять допишем в частное цифру 1 и получим следующий результат (для экономии места сразу опустим следующую цифру).

 

Полученное число 110 больше 101, поэтому и на этом шаге мы запишем в частное 1. Получиться так:

-
	-
			-

Полученное число 11 меньше 101, поэтому записываем в частное цифру 0 и опускаем вниз следующую цифру. Получается так:

-

-

-

Полученное число больше 101, поэтому в частное записываем цифру 1 и опять выполняем действия. Получается такая картина:

-

-

-

-

Полученный остаток 10 меньше 101, но у нас закончились цифры в делимом, поэтому 10 это окончательный остаток, а 1110 это искомое частное.

Проверим в десятичных числах

10010011 = 147 101 = 5

10 = 2 11101 = 29

-
	-

На этом мы заканчиваем описание простейших арифметических операций, которые необходимо знать, для того, чтобы пользоваться двоичной арифметикой, и теперь попробуем ответить на вопрос "Зачем нужна двоичная арифметика". Конечно, выше уже было показано, что запись числа в двоичной системе существенно упрощает арифметические операции, но в то же время сама запись становится значительно длиннее, что уменьшает ценность полученного упрощения, поэтому необходимо поискать такие задачи, решение которых существенно проще в двоичных числах.

Самостоятельная работа № 4

1. Выполните сложение, вычитание, умножение в двоичной системе счисления:

1.1111 и 1011;
2.1001 и 110;
3.11001 и 10111;
4.111 и 101;
5.10011 и 1101;
6.10011 и 1001;
7.110110 и 11111;
8.10011001 и 1101;
9.10101 и 1101;
10. 10111и 111;
11.11001и 111;
12.10111 и 111100;
13.11000 и 1101;
14.1011и 111.
15.1100100 и 100011;
16.101101 и 1101;

 

Ответ: __________________

2. Выполните деление в двоичной системе счисления:

1. 10100101: 1011=
2. 10100101:1111=
3. 110110:110=
4. 110110:1001=
5. 1000111111:11001=
6. 1000111111:10111=
7. 11110111:10011=
8. 11110111:1101=
9. 10101011: 10011=
10. 10101011: 1001=
11. 10100001:111=
12. 10100001:10111=
13. 10101111:111=
14. 10101111:11001=
15. 1001101:1011=
16. 1001101:111=

Ответ: __________________

Контрольная работа по теме «Системы счисления»

В-1.

№ 1.

Представьте в развернутой форме:

а) 4563 ; б) 100101 ;

№ 2.

Переведите число 75 из десятичной системы счисления в двоичную.

№ 3.

Выполните действия:

а) 11001101011 + 1110000101 ; б) 101011 – 10011 ; в) 1011 · 101 .

В-2.

№ 1

Представьте в развернутой форме:

а) 1563 ; б) 100111 ;

№ 2.

Переведите число 67 из десятичной системы счисления в двоичную.

№ 3.

Выполните действия:

а) 11001101111 + 1110000101 ; б) 10111 – 10011 ; в) 1111 · 101 .

В-3.

№ 1

Представьте в развернутой форме:

а) 2563 ; б) 110101 ;

№ 2.

Переведите число 59 из десятичной системы счисления в двоичную.

№ 3.

Выполните действия:

а) 11111101011 + 1110000111 ; б) 11111 – 10011 ; в) 10011 · 101 .

В-4.

№ 1

Представьте в развернутой форме:

а) 2573 ; б) 1010101 ;

№ 2.

Переведите число 95 из десятичной системы счисления в двоичную.

№ 3.

Выполните действия:

а) 11111101001 + 1110000111 ; б) 11101 – 10011 ; в) 10111 · 101 .

 

Дополнительный раздел: «Занимательно и интересно!»

А) Рисуем по точкам.

В таблице 1 приведены номер точки и ее координаты, записанные в двоичной системе счисления.
Для каждой точки выполните перевод ее координат в десятичную систему счисления и отметьте точку на координатной плоскости. Правильно сделав перевод и соединив последовательно все точки, вы получите некоторый рисунок. Рисунок изобразите в рабочей тетради.

 

 

 

Таблица 1

№ точки	Координаты точки	(X;Y)
X	Y
	1002	102
	1012	1012
	12	1012
	112	10102
	1002	10102
	112	1102
	1012	1102
	1102	1012 + 1002
	1112	10012
	1102	1102
	1002 * 102	1102
	10002	1012
	1102	1012
	1012	102

Б) Рождение цветка.

Понаблюдаем за рождением цветка: сначала появился один листочек, затем второй … и вот распустился бутон. Постепенно подрастая, цветок показывает нам некоторое двоичное число. Если вы до конца проследите за ростом цветка, то узнаете, сколько дней ему понадобилось, чтобы вырасти.

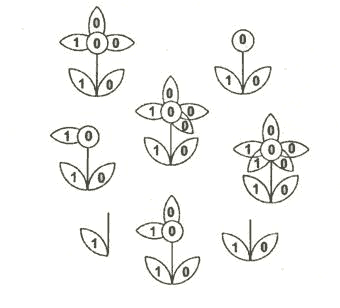
Ответ: ______________

В) Русская поговорка.

Здесь зашифрована известная русская поговорка. Прочитайте ее, двигаясь с помощью двоичных цифр в определенной последовательности.

 

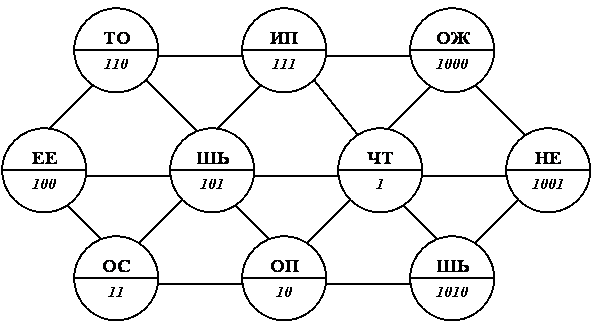
Ответ: ____________________________________________

 

Для любознательных

Ещё два способа преобразования чисел 10-й в 2-ую систему счисления:

I. Метод вычитания

С детства мы считать учились – раз, два, три, четыре, пять

Десятичной ту систему мы привыкли называть.

Были палочки и счеты, калькулятор, Пифагор,

А теперь перед глазами – серебристый монитор.

Эта умная машина сможет все нам сосчитать

Ну, а как она считает – предстоит нам разобрать.

Мы считаем в десятичной – два, двенадцать, сто один,

А компьютер лишь в двоичной – либо ноль, либо один.

Разберемся на примере: число будет – сорок пять

Наибольшую здесь степень нам придется сосчитать

Раз считаем мы в двоичной основанье всегда два

Показатель мы находим от начального числа.

И поскольку изначально наша цифра сорок пять,

32=25

Мы подумаем и скажем показатель будет пять.

В показателе пятерка в основанье цифра два

8=23

Возведем мы двойку в степень и получим 32.

4=22

Возвращаемся мы снова к нашей цифре 45

1=20

Нам теперь от этой цифры 32 нужно отнять.

Разность сосчитать нам просто мы уже не первый класс

Видим: циферка 13 получается у нас.

Теперь циферку 13 также как и 45

Вместе с вами нам придется разложить и посчитать

Снова в основанье двойка показатель будет три

Двойка в третьей будет восемь ну, а дальше сам смотри.

У 45-ти два в пятой умножаем на один

У 13 два в третьей тоже множим на один

Два в четвертой не встречалась, тут и нечего гадать

Значит, будем два в четвертой мы на нолик умножать.

Запись: 45₁₀ = 1*2⁵+0*2⁴+1*2³+1*2²+0*2¹+1*2⁰ =101101₂

Подводим итог: Необходимо разложить данное нам число по степеням «2». В том случае, если полная степень «2» присутствует при разложении, сомножителем будет единица, если степени «2» нет – сомножитель ноль. Важно! При записи числа в «2»-ой системе счисления нельзя пропускать ни одну степень.

II. Метод степеней

Разберем еще один пример: Перевести из «10»-ой системы счисления в «2»-ю число 23. Какие степени «2» представлены в этом числе?

1) Ищем максимальную степень «2» – это 2⁴ =16. Итак: 23-16=7

2) Для числа 7 подбираем максимальную степень это 2² =4. Вычитаем 7-4=3.

3) Для числа 3 подбираем максимальную степень это 2¹ =2. Вычитаем 3-2=1.

4) Для числа 1 остался единственный вариант это степень 2⁰ =1.

Теперь можем записать разложение числа 23 по степеням «2»:

Запись: 23₁₀ =1*2⁴ +0*2³ +1*2² +1*2¹ +1*2⁰