• Вектор магнитной индукции
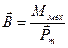 ,
,
где 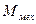 - механический момент контура с током,
- механический момент контура с током,  -магнитный момент контура с током, S- площадь контура,
-магнитный момент контура с током, S- площадь контура, 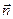 - нормаль к поверхности;
- нормаль к поверхности;
• Связь вектора магнитной индукции с напряженностью магнитного поля
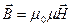 .
.
• Принцип суперпозиции магнитных полей
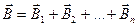 ;
;
В случае двух полей  ;
;
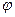 - угол между
- угол между 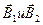 ;
;
• Закон Био-Савара-Лапласа
Индукция магнитного поля, создаваемая элементом проводника  с током
с током 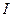 в некоторой точке равна
в некоторой точке равна
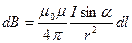 ,
,
где 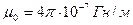 -магнитная постоянная,
-магнитная постоянная, 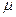 - магнитная проницаемость среды,
- магнитная проницаемость среды,  - длина элемента проводника,
- длина элемента проводника, 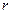 - расстояние от середины элемента проводника до точки, в которой определяется магнитная индукция,
- расстояние от середины элемента проводника до точки, в которой определяется магнитная индукция,  - угол между элементом проводника
- угол между элементом проводника  и r;
и r;
• Магнитное поле бесконечного прямого тока 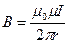 .
.
• Магнитное поле в центре кругового витка с током радиуса r
 .
.
• Сила Ампера (сила, действующая на прямолинейный проводник с током в магнитном поле)
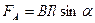 ,
,
где I – сила тока, В- магнитная индукция, 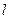 - длина проводника,
- длина проводника,  - угол между
- угол между 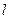 и
и 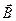 ;
;
• Сила Лоренца (сила, действующая со стороны магнитного поля на заряд, движущийся со скорость  )
)
 ,
,
где  - угол между
- угол между  и
и 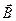 ;
;
• Закон электромагнитной индукции (закон Фарадея)
 ,
, 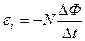 ,
, 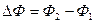 ,
,
где  - электродвижущая сила индукции, N – число витков контура, Ф – магнитный поток, пронизывающий поверхность, ограниченную контуром,
- электродвижущая сила индукции, N – число витков контура, Ф – магнитный поток, пронизывающий поверхность, ограниченную контуром, 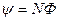 - потокосцепление;
- потокосцепление;
• Работа по перемещению проводника с током в магнитном поле
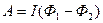 .
.
• Магнитный поток в однородном поле 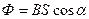 .
.
Магнитный поток сцепленный с контуром 
• Потокосцепление контура
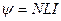 ,
,
где L – индуктивность контура, 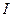 - сила тока.
- сила тока.
•Электродвижущая сила самоиндукции
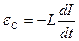 ,
, 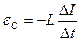 ;
;
• Индуктивность соленоида
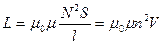 .
.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Контрольная работа №2
Задача 9. Два заряда взаимодействуют в вакууме на расстоянии 
 м с такой же силой, как и в трансформаторном масле на расстоянии 0,48см. Определить диэлектрическую проницаемость трансформаторного масла.
м с такой же силой, как и в трансформаторном масле на расстоянии 0,48см. Определить диэлектрическую проницаемость трансформаторного масла.
 Дано: Решение
Дано: Решение
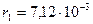 м Сила взаимодействия зарядов определяется законом Кулона
м Сила взаимодействия зарядов определяется законом Кулона
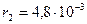 м Для зарядов, находящихся в вакууме, закон Кулона
м Для зарядов, находящихся в вакууме, закон Кулона
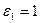 записывается
записывается 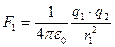 ,
,
______________ Для зарядов, находящихся в трансформаторном масле,

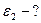 закон Кулона имеет вид
закон Кулона имеет вид 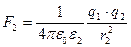 .
.
По условию 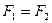 , тогда
, тогда
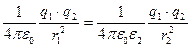 , откуда
, откуда
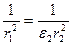 . Диэлектрическая проницаемость трансформаторного масла
. Диэлектрическая проницаемость трансформаторного масла
определяется как  . Размерность очевидна.
. Размерность очевидна.
Вычисления
 .
.
Ответ: 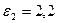 .
.
Задача 10. В трёх вершинах квадрата со стороной 40см находятся одинаковые положительные заряды по 5 нКл каждый. Найти напряженность поля, создаваемого этими зарядами, в четвёртой вершине.
 Дано: Решение
Дано: Решение
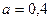 м
м
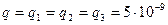 Кл
Кл

_____________________

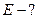
По принципу суперпозиции напряженность поля, создаваемого несколькими зарядами, в некоторой точке равна геометрической сумме напряженностей полей, создаваемых каждым зарядом, т.е  . (1)
. (1)
Записываем уравнение (1) в проекциях на выбранные направления Х и У:
 ,
, 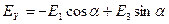 , (2)
, (2)
Проекция 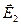 на ось У равна нулю, так как
на ось У равна нулю, так как 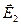 перпендикулярна оси У.
перпендикулярна оси У.
По определению напряженности 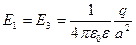 ,
, 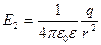 .
.
Расстояние от второй вершины до четвёртой находим по теореме Пифагора
 , тогда
, тогда 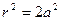 . Поскольку заряды находятся в вершинах квадрата, то
. Поскольку заряды находятся в вершинах квадрата, то 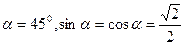 . Так как
. Так как 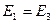 и
и 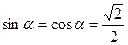 , то
, то
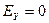 . Отсюда
. Отсюда
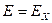
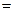

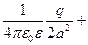
 =
= 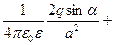
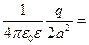
=  .
.
Проверка размерности
 .
.
Вычисления
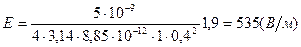
Ответ: 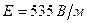 .
.
Задача 11. Два шарика с зарядами 6,7 нКл и 13,3 нКл находятся на расстоянии 40 см друг от друга. Какую работу надо совершить, чтобы сблизить их до расстояния 25 см?
 Дано: Решение
Дано: Решение
 Кл В задачах такого типа нужно считать один из зарядов
Кл В задачах такого типа нужно считать один из зарядов
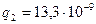 Кл неподвижным, образующим электрическое поле, а другой-
Кл неподвижным, образующим электрическое поле, а другой-
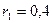 м - движущимся в поле первого заряда.
м - движущимся в поле первого заряда.

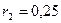 м Пусть заряд
м Пусть заряд  неподвижен и создает поле, а шарик с
неподвижен и создает поле, а шарик с
 зарядом
зарядом 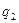 движется в этом поле из точки, находящейся на
движется в этом поле из точки, находящейся на
______________ расстоянии 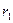 от шарика с зарядом
от шарика с зарядом  , в точку,
, в точку,
 А-? находящуюся на расстоянии
А-? находящуюся на расстоянии 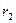 от него. Тогда работа,
от него. Тогда работа,
которую совершает внешняя сила
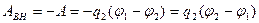 , (1)
, (1)
где 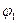 и
и 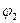 - потенциалы начальной и конечной точек поля. Поскольку поле образовано зарядом
- потенциалы начальной и конечной точек поля. Поскольку поле образовано зарядом  , то потенциалы
, то потенциалы
 и
и 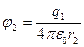 (2)
(2)
Подставляем (2) в (1):
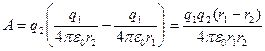 .
.
Проверка размерности
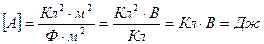
Вычисления
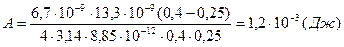
Ответ: 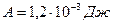 .
.
Задача 12. Плоский воздушный конденсатор, расстояние между пластинами которого 5 см, заряжен до 200В и отключен от источника напряжения. Каким будет напряжение на конденсаторе, если его пластины раздвинуть до 10 см?
 Дано: Решение
Дано: Решение
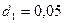 м По определению ёмкость плоского конденсатора
м По определению ёмкость плоского конденсатора
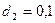 м и напряжение на нем до раздвижения пластин
м и напряжение на нем до раздвижения пластин
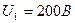
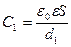 ,
, 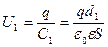 . (1)
. (1)
______________ При раздвижении пластин заряд на конденсаторе не
 изменяется, так как конденсатор отключен от напряжения.
изменяется, так как конденсатор отключен от напряжения.
Емкость и напряжение после раздвижения пластин
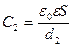 ,
, 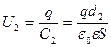 . (2)
. (2)
Разделим почленно выражение (1) на (2)
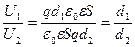 , отсюда
, отсюда 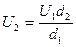 .
.
Проверка размерности
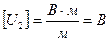
Вычисления

Ответ: 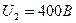 .
.
Задача 13. Источник тока с ЭДС равной 2,1В и внутренним сопротивлением
0,2 Ом соединен с реостатом. Определить силу тока в цепи и сопротивление реостата, если напряжение на зажимах источника тока 2В. Какой длины надо взять для изготовления реостата железную проволоку, если площадь её сечения 0,75 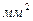 ?
?
Дано: Решение
 По закону Ома сила тока для замкнутой цепи определяется
По закону Ома сила тока для замкнутой цепи определяется
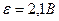 как
как 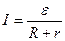 . (1)
. (1)
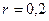 Ом Для участка цепи, состоящего из реостата закон Ома
Ом Для участка цепи, состоящего из реостата закон Ома
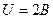
 . (2)
. (2)
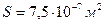 Находим сопротивление реостата, решая совместно (1) и (2)
Находим сопротивление реостата, решая совместно (1) и (2)
______________ 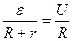 ,
, 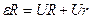 ,
,  , откуда
, откуда
I-? R-? L-? сопротивление реостата  .
.
Найдем длину проволоки, используя формулу
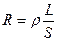 , где удельное сопротивление железа
, где удельное сопротивление железа 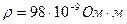 .
.
 .
.
Проверка размерности
 ,
, 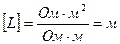 .
.
Вычисления
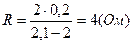 ,
, 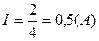 ,
, 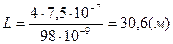
Ответ: 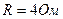 ,
,  ,
, 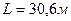 .
.
Задача 14. Батарея состоит из параллельно соединенных элементов. При силе тока во внешней цепи 2 А полезная мощность равна 7 Вт.Определить число элементов в батарее, если ЭДС каждого элемента 5,5 В, а внутреннее сопротивление 5 Ом.
 Дано: Решение
Дано: Решение
Полезная мощность, выделяемая на сопротивлении R:

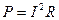 . Найдем сопротивление R, используя закон Ома
. Найдем сопротивление R, используя закон Ома
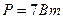 для замкнутой цепи
для замкнутой цепи 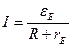 . Из данного выражения
. Из данного выражения
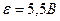

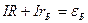 ,
, 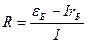 , где
, где 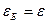 - ЭДС батареи,
- ЭДС батареи,
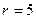 Ом состоящей из n одинаковых параллельно соединенных
Ом состоящей из n одинаковых параллельно соединенных
______________ элементов. При параллельном соединении внутреннее
n -? сопротивление батареи 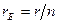 .
.
Подставив выражения для 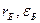 и
и 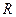 в формулу для полезной мощности, получаем
в формулу для полезной мощности, получаем
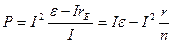 , откуда
, откуда 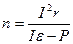 .
.
Проверка размерности
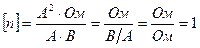 (безразмерная величина)
(безразмерная величина)
Вычисления
.
Ответ: 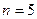 .
.
Задача 15. В однородном магнитном поле с индукцией 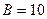 мТл висит алюминиевый проводник диаметром d=0,2 мм. Определить силу тока в проводнике. Плотность алюминия
мТл висит алюминиевый проводник диаметром d=0,2 мм. Определить силу тока в проводнике. Плотность алюминия 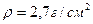 .
.
 Дано: Решение
Дано: Решение
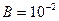 Тл На проводник действуют две силы: сила тяжести и сила
Тл На проводник действуют две силы: сила тяжести и сила 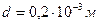 Ампера, которые уравновешивают друг друга и проводник
Ампера, которые уравновешивают друг друга и проводник
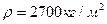 остается в покое, т.е.
остается в покое, т.е.  . (1)
. (1)
 ________ Сила Ампера
________ Сила Ампера 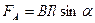 , (2) где
, (2) где  - длина проводника.
- длина проводника.
I -? Масса проводника 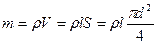 . (3) Подставляем
. (3) Подставляем
выражения (2) и (3) в (1)
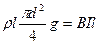 , т.к.
, т.к. 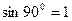 .
.
Сила тока в проводнике 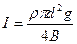 .
.
Проверка размерности
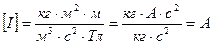 .
.
Вычисления
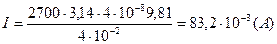 .
.
Ответ:  .
.
Задача 16. Вычислить радиус R дуги окружности, которую описывает протон в магнитном поле с индукцией В=15 мТл, если скорость протона равна 2 Мм/с.
 Дано: Решение
Дано: Решение
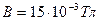 Попадая в магнитное поле, протон будет двигаться
Попадая в магнитное поле, протон будет двигаться
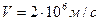 по дуге окружности радиуса
по дуге окружности радиуса 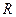 . Протон – положительно
. Протон – положительно
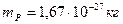 заряженная частица. В магнитном поле на протон будет
заряженная частица. В магнитном поле на протон будет
______________ действовать сила Лоренца. Согласно второму закону
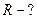 Ньютона
Ньютона  .
. 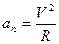 - нормальное ускорение,
- нормальное ускорение,
направленное по радиусу к центру окружности.
 , т.к.
, т.к. 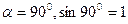 .
.
Заряд протона 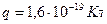 .
.
Радиус окружности 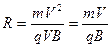 .
.
Проверка размерности
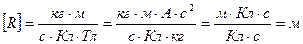 .
.
Вычисления
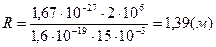 .
.
Ответ: 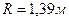 .
.
ЗАДАЧИ
200. Два шарика массами по 0,1 г подвешены в одной точке на нитях длиной по 20 см каждая. Получив одинаковый заряд, шарики разошлись так, что нити образовали между собой угол 60 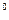 . Определить заряд каждого шарика.
. Определить заряд каждого шарика.
201. Даны два шарика массами по 1 г каждый. Какой заряд нужно сообщить каждому шарику, чтобы сила взаимного отталкивания зарядов уравновесила силу гравитационного притяжения шариков? Рассматривать шарики как материальные точки, которые находятся в воздухе.
202. Расстояние между точечными зарядами +9q и + q равно 8 см. На каком расстоянии от первого заряда находится точка, в которой напряженность поля зарядов равна нулю? Где находилась бы эта точка, если бы второй заряд был отрицательным?
203. В вершинах квадрата находятся одинаковые заряды по 3·10 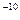 Кл каждый. Какой отрицательный заряд нужно поместить в центре квадрата, чтобы сила взаимного отталкивания положительных зарядов была уравновешена силой притяжения отрицательного заряда?
Кл каждый. Какой отрицательный заряд нужно поместить в центре квадрата, чтобы сила взаимного отталкивания положительных зарядов была уравновешена силой притяжения отрицательного заряда?
204. Точечный заряд q = 10 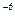 Кл находится вблизи большой равномерно заряженной пластины против её середины. Определить поверхностную плотность заряда пластины, если на точечный заряд действует сила 60 Н.
Кл находится вблизи большой равномерно заряженной пластины против её середины. Определить поверхностную плотность заряда пластины, если на точечный заряд действует сила 60 Н.
205. Два шарика одинаковых радиуса и массы подвешены на нитях одинаковой длины так, что их поверхности соприкасаются. Какой заряд q нужно сообщить шарикам, чтобы сила натяжения нитей стала равной
Т = 98 мН? Расстояние от центра шарика до точки подвеса l = 10 см; масса каждого шарика m = 5 г.
206. На бесконечной заряженной плоскости закреплена нить, на конце которой висит одноименно заряженный шарик массой 0,4 г и зарядом 667пКл. Сила натяжения нити Т = 0,49 мН. Найти поверхностную плотность заряда σ на плоскости.
208. В трёх вершинах квадрата со стороной 40 см находятся одинаковые положительные заряды по 5нКл каждый. Найти напряженность поля в четвёртой вершине.
209. Стальной шар радиусом 0,5 см, погружённый в керосин, находится в однородном электрическом поле напряжённостью 35 кВ/см, направленной вертикально вверх. Определить заряд шара, если он находится во взвешенном состоянии.
210. Две параллельные плоские пластины, находящиеся на расстоянии 10 см друг от друга, заряжены до разности потенциалов 1кВ. Какая сила будет действовать на заряд 10 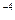 Кл, помещённый между пластинами?
Кл, помещённый между пластинами?
211. Найти потенциал φ точки поля, находящейся на расстоянии r = 10 см от центра заряженного шара радиусом R = 1 см. Задачу решить, если: а) задана поверхностная плотность заряда на шаре σ = 0,1 мкКл/м2; б) задан потенциал шара φ0 = 300 В.
213. Расстояние между зарядами 1 нКл и 6,67 нКл равно 10 см. Какую работу надо совершит, чтобы перенести второй заряд в точку, находящуюся от первого заряда на расстоянии 1 м?
214. При радиоактивном распаде из ядра атома полония вылетает α - частица со скоростью 1,6·10  см/с. Какую разность потенциалов надо приложить, чтобы сообщить α – частице такую же скорость?
см/с. Какую разность потенциалов надо приложить, чтобы сообщить α – частице такую же скорость?
215. Какая работа А совершается при перенесении точечного заряда q = 20 нКл из бесконечности в точку, находящуюся на расстоянии r = 1 см от поверхности шара радиусом R = 1 см с поверхностной плотностью заряда σ = 10 мкКл/м2?
216. Шарик с массой m = 1 г и зарядом q = 10 нКл перемещается из точки 1, потенциал которой φ1 = 600 В, в точку 2, потенциал которой φ2 = 0. Найти его скорость в точке 1, если в точке 2 она стала равной V2 = 20 см/с.
217. Около заряженной бесконечно протяженной плоскости находится точечный заряд q = 0,66 нКл. Заряд перемещается по линии напряженности поля на расстояние ∆R = 2 см; при этом совершается работа А = 5·10  Дж. Найти поверхностную плотность заряда σ на плоскости.
Дж. Найти поверхностную плотность заряда σ на плоскости.
218. Расстояние между зарядами 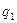 = +1мкКл и
= +1мкКл и 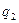 = -1мкКл равно 10 см. Определить потенциал поля в точке, удалённой на расстояние 10 см от первого заряда и лежащей на линии, проходящей через первый заряд перпендикулярно к направлению от
= -1мкКл равно 10 см. Определить потенциал поля в точке, удалённой на расстояние 10 см от первого заряда и лежащей на линии, проходящей через первый заряд перпендикулярно к направлению от 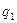 к
к 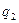 .
.
219. Пылинка массой 10 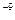 г, несущая на себе 5 электронов, прошла в вакууме ускоряющую разность потенциалов 3·10
г, несущая на себе 5 электронов, прошла в вакууме ускоряющую разность потенциалов 3·10 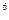 В. Какую скорость приобрела пылинка? Какова кинетическая энергия пылинки в электронвольтах?
В. Какую скорость приобрела пылинка? Какова кинетическая энергия пылинки в электронвольтах?
220. В плоский конденсатор вдвинули плитку парафина толщиной 1 см, который вплотную прилегает к его пластинам. На сколько нужно увеличить расстояние между пластинами, чтобы получить прежнюю ёмкость?
221. Ёмкость плоского конденсатора 1,5 мкФ. Расстояние между пластинами 5 мм. Какова будет ёмкость конденсатора, если на нижнюю пластину положить лист эбонита толщиной 3 мм?
222. Между пластинами плоского конденсатора, заряженного до разности потенциалов 600 В, находятся два слоя диэлектрика: стекла толщиной 7 мм и эбонита толщиной 3 мм. Площадь каждой пластины конденсатора 200 см 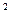 . Определить: а) элетроёмкость конденсатора; б) падение потенциала в каждом слое.
. Определить: а) элетроёмкость конденсатора; б) падение потенциала в каждом слое.
223. Два конденсатора ёмкостью 3 мкФ и 6 мкФ соединены между собой и присоединены к батарее с ЭДС 120 В. Определить заряд каждого конденсатора и разность потенциалов между его обкладками, если конденсаторы соединены: а) параллельно; б) последовательно.
224. Расстояние между пластинами плоского конденсатора 2 см, разность потенциалов 6000 В. Заряд каждой пластины 10 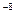 Кл. Определить энергию поля конденсатора и силу взаимного притяжения пластин.
Кл. Определить энергию поля конденсатора и силу взаимного притяжения пластин.
225. Найти ёмкость С сферического конденсатора, состоящего из двух концентрических сфер с радиусами r = 10 см и R= 10,5 см. Пространство между сферами заполнено маслом. Какой радиус R0 должен иметь шар, помещенный в масло, чтобы иметь такую же ёмкость?
226. Плоский воздушный конденсатор ёмкостью 1000 пФ заряжен до разности потенциалов 300 В. После отключения от источника напряжения расстояние между пластинами конденсатора было увеличено в 5 раз. Определить: а) разность потенциалов на обкладках конденсатора после раздвижения; б) работу внешних сил по раздвижению пластин.
227. Три одинаковых плоских конденсатора соединены последовательно. Ёмкость такой батареи конденсаторов 8 пФ. Площадь каждой пластины
100 см 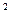 ., диэлектрик – стекло. Определить толщину стекла.
., диэлектрик – стекло. Определить толщину стекла.
228. Конденсатор, заряженный до напряжения 100 В, соединяется параллельно с конденсатором той же ёмкости, но заряженным до напряжения 200 В. Какое напряжение установится между обкладками?
229. Какое количество теплоты выделится при разряде плоского конденсатора, если разность потенциалов между пластинами 15000 В, расстояние 1 мм, диэлектрик – слюда и площадь каждой пластины 300 см 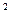 .
.
230. К элементу с ЭДС 1,5 В присоединили катушку с сопротивлением 0,1 Ом. Амперметр показал силу тока, равную 0,5 А. Когда к элементу присоединили последовательно ещё один элемент с такой же ЭДС, то сила тока в той же катушке оказалась 0,4 А. Определить внутреннее сопротивление первого и второго элементов.
231. Две группы из трёх последовательно соединенных элементов соединены параллельно. ЭДС каждого элемента 1,2 В, внутреннее сопротивление 0,2 Ом.. полученная батарея замкнута на внешнее сопротивление 1,5 Ом. Определить силу тока во внешней цепи и КПД батареи.
232. Ток I в проводнике меняется со временем t по уравнению I= 4+2t, где I – в амперах и t в секундах. Какое количество электричества q проходит через поперечное сечение проводника за время от t1 = 2 с до t2 = 6 с? При каком постоянном токе I0 через поперечное сечение проводника за то же время проходит такое же количество электричества?
233. Зашунтированный амперметр измеряет токи силой до 10 А. Какую наибольшую силу тока может измерить этот амперметр без шунта, если сопротивление амперметра 0,02 Ом и сопротивление шунта 0,005 Ом?
234. Катушка и амперметр соединены последовательно и присоединены к источнику тока. К зажимам катушки присоединён вольтметр с сопротивлением 1000Ом. Показание амперметра 0,5 А, вольтметра 100 В. Определить сопротивление катушки. Сколько процентов от точного значения сопротивления катушки составит ошибка, если не учитывать сопротивление катушки?
235. Дано 12 элементов с ЭДС 1,5 В и внутренним сопротивлением 0,4 Ом. Как нужно соединить эти элементы, чтобы получить от собранной из них батареи наибольшую силу тока во внешней цепи, имеющей сопротивление 0,3 Ом? Скольким амперам равна наибольшая сила тока?
236. ЭДС батареи равна 12 В., сила тока короткого замыкания 5 А. Какую наибольшую мощность может дать батарея во внешней цепи?
237. К зажимам батареи аккумуляторов присоединён нагреватель. ЭДС батареи равна 24 В, внутреннее сопротивление 1 Ом. Нагреватель, включённый в цепь. Потребляет мощность 80 Вт. Определить силу тока в цепи и КПД нагревателя.
238. При силе тока 3 А во внешней цепи батареи выделяется мощность 18 Вт, при силе тока 1 А – 10 Вт. Определить ЭДС и внутреннее сопротивление батареи.
239. Три батареи с ЭДС 12 В, 5 В, 10 В и одинаковыми внутренними сопротивлениями, равными 1 Ом, соединены между собой одноименными полюсами. Сопротивление соединительных проводов ничтожно мало. Определить силы токов, идущих через батареи.
240. Определить ЭДС и внутреннее сопротивление аккумулятора, если при силе тока 5 А от дает во внешнюю цепь мощность 9,5 Вт, а при силе тока 8 А во внешней цепи выделяется 14,4 Вт.
241. В электрической цепи при внешних сопротивлениях 2 Ом и 0,1 Ом выделяется одинаковая мощность. Найти внутреннее сопротивление источника.
242. Три проводника, сопротивления которых соответственно равны 3 Ом,
6 Ом и 8 Ом, соединены параллельно. В первом проводнике выделяется 21 кДж тепла. Определить количество теплоты, выделяющееся во втором и третьем проводниках за то же время.
243. В медном проводнике длиной 2 м и площадью поперечного сечения
0,4 мм 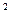 идет ток. При этом ежесекундно выделяется 0,35 Дж теплоты. Сколько электронов проходит за 1 с через поперечное сечение этого проводника?
идет ток. При этом ежесекундно выделяется 0,35 Дж теплоты. Сколько электронов проходит за 1 с через поперечное сечение этого проводника?
244. Какой длины нужно взять нихромовый проводник диаметром 0,5 мм, чтобы изготовить электрический камин, работающий пр напряжении 120 В и дающий 1 МДж теплоты в час?
245. На электроплитку мощностью 600 Вт поставили кастрюлю, имеющую 1 л воды и 0,5 кг льда при 0 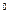 С. Через сколько времени температура в кастрюле поднимется до 60
С. Через сколько времени температура в кастрюле поднимется до 60 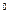 С, если КПД плитки 60%?
С, если КПД плитки 60%?
246. Определить сопротивление подводящих проводов от источника с напряжением 120 В, если при коротком замыкании предохранители из свинцовой проволоки площадью сечения 1 мм 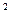 и длиной 2 см плавятся за 0,03 с. Начальная температура предохранителя 27
и длиной 2 см плавятся за 0,03 с. Начальная температура предохранителя 27  С.
С.
247. Найти КПД источника тока с внутреннем сопротивлением 0,1 Ом, если он работает на нагрузку с сопротивлением 1,5 Ом.
248. К зажимам батареи аккумуляторов присоединен нагреватель. ЭДС батареи равна 24 В, внутреннее сопротивление r = 1 Ом. Нагреватель, включенный в цепь потребляет мощность 80 Вт. Вычислить силу тока I и КПД нагревателя.
249. Полезная мощность, выделяемая во внешней части цепи, достигает наибольшего значения 5 Вт при силе тока 5 А. Найти внутреннее сопротивление и ЭДС источника тока.
250. Очень короткая катушка содержит N = 1000 витков тонкого провода. Катушка имеет квадратное сечение со стороной а = 10 см. Найти магнитный момент 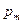 катушки при силе тока 1 А.
катушки при силе тока 1 А.
251. Проволочный виток радиусом R=5 см находится в однородном магнитном поле напряженностью Н = 2 кА/м. Плоскость витка образует угол
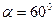 с направлением поля. По витку течет ток 4 А. Найти механический момент М, действующий на рамку.
с направлением поля. По витку течет ток 4 А. Найти механический момент М, действующий на рамку.
252. Прямой провод длиной 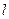 =10 см, по которому течет ток I =20 А, находится в однородном магнитном поле с индукцией В=0,01 Тл. Найти угол
=10 см, по которому течет ток I =20 А, находится в однородном магнитном поле с индукцией В=0,01 Тл. Найти угол 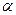 между направлением вектора
между направлением вектора  и тока, если на провод действует сила
и тока, если на провод действует сила
F= 10 мН.
253. Вычислить радиус R дуги окружности, которую описывает протон в магнитном поле с индукцией В=15 мТл, если скорость протона равна 2 Мм/с.
254. Ион, несущий один элементарный заряд, движется в однородном магнитном поле с индукцией В=0,015 Тл по окружности радиусом R=10 см. Определить импульс иона.
255. По двум параллельным проводам длиной 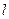 =1м каждый текут одинаковые токи. Расстояние d между проводами равно 1 см. Токи взаимодействуют с силой F=1 мН. Найти силу тока в проводах.
=1м каждый текут одинаковые токи. Расстояние d между проводами равно 1 см. Токи взаимодействуют с силой F=1 мН. Найти силу тока в проводах.
256. Частица. Несущая один элементарный заряд, влетела в однородное магнитное поле с индукцией В=0,5 Тл. Определить момент импульса L, которым обладала частица при движении в магнитном поле, если её траектория представляла дугу окружности радиусом R=0,2 см.
257. Протон, прошедший ускоряющую разность потенциалов U=600 В, влетел в однородное магнитное поле с индукцией В=0,3 Тл и начал двигаться по окружности. Вычислить её радиус R.
258. По тонкому проводу в виде кольца радиусом R=20 см течет ток 100 А. Перпендикулярно плоскости кольца возбуждено однородное магнитное поле с индукцией В=20 мТл. Найти силу F, растягивающую кольцо.
259. Заряженная частица, обладающая скоростью 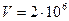 м/с, влетела в однородное магнитное поле с индукцией В=0,52 Тл. Найти отношение
м/с, влетела в однородное магнитное поле с индукцией В=0,52 Тл. Найти отношение  заряда частицы к её массе, если частица в поле описала дугу окружности радиусом R=4 см. По этому отношению определить, какая это частица.
заряда частицы к её массе, если частица в поле описала дугу окружности радиусом R=4 см. По этому отношению определить, какая это частица.
ПРИЛОЖЕНИЕ






