Этих границ в нормативно-технической документации

Пределы допускаемой основной и дополнительных погрешностей определяются разработчиками для каждого типа средств измерений на стадии подготовки производства. В зависимости от назначения средства измерений и характера изменения погрешности в пределах диапазона измерений нормируется для средств измерений различного типа либо предельно-допустимое значение основной абсолютной погрешности, либо предельно-допустимое значение основной приведенной погрешности, либо предельно-допустимое значение основной относительной погрешности.

Для каждого типа средств измерений характер изменения погрешности в пределах диапазона измерений зависит от принципа действия этого средства измерений и может быть самым разнообразным. Однако, как показала практика, среди этого многообразия часто удается выделить три типовых случая, предопределяющих выбор формы представления пределов допускаемой погрешности. Типовые варианты отклонения реальных передаточных характеристик средств измерений от номинальной характеристики и соответствующие им графики изменения предельных значений абсолютной и относительной погрешностей в зависимости от измеряемой величины приведены на рис 2.

 

 

 

Если реальная передаточная характеристика средства измерений смещена по отношению к номинальной (1-й график на рис.2а), абсолютная погрешность, возникающая при этом, (1-й график на рис.2б), не зависит от измеряемой величины.

 

Составляющую погрешности средства измерений, не зависящую от измеряемой величины, называют аддитивной погрешностью.

Если угол наклона реальной передаточной характеристики средства измерений отличается от номинального (2-й график на рис. 2а), то абсолютная погрешность будет линейно зависеть от измеряемой величины (2-й график на рис. 2б).

 

Составляющую погрешности средства измерений, линейно зависящую от измеряемой величины, называют мультипликативной погрешностью.

Если реальная передаточная характеристика средства измерений смещена по отношению к номинальной и угол ее наклона отличается от номинального (3-й график на рис. 2а), то в этом случае имеет место как аддитивная, так и мультипликативная погрешность.

Аддитивная погрешность возникает из-за неточной установки нулевого значения перед началом измерений, ухода нуля в процессе измерений, из-за наличия трений в опорах измерительного механизма, из-за наличия термо-эдс в контактных соединениях и т.д.

Мультипликативная погрешность возникает при изменении коэффициентов усиления или ослабления входных сигналов (например, при изменении температуры окружающей среды, или вследствие старения элементов), из-за изменения значений, воспроизводимых мерами, встроенными в измерительные приборы, из-за изменений жесткости пружин, создающих противодействующий момент в электромеханических приборах и т.д.

Ширина полосы неопределенности значений абсолютной (рис.2б) и относительной (рис.2в) погрешностей характеризует разброс и изменение в процессе эксплуатации индивидуальных характеристик множества находящихся в обращении средств измерений определенного типа.

 

А) Нормирование пределов допускаемой основной погрешности для

средств измерений с преобладающей аддитивной погрешностью.

Для средств измерений с преобладающей аддитивной погрешностью (1-й график на рис.2) удобно нормировать одним числом предельно-допустимое значение абсолютной погрешности (∆_max= ±а). В этом случае фактическая абсолютная погрешность ∆ каждого экземпляра средства измерений данного типа на различных участках шкалы может иметь различные значения, но не должна превышать предельно-допустимой величины (∆ ≤ ±а). В многопредельных измерительных приборах с преобладающей аддитивной погрешностью для каждого предела измерений пришлось бы указывать свое значение предельно допустимой абсолютной погрешности. К сожалению, как видно из 1-го графика на рис.2в, нормировать одним числом предел допускаемой относительной погрешности в различных точках шкалы не представляется возможным. По этой причине для средств измерений с преобладающей аддитивной погрешностью часто нормируют одним числом значение так называемой основной приведеннойотносительной погрешности

,

где X_N – нормирующее значение.

Таким способом, например, нормируются погрешности большинства электромеханических и электронных приборов со стрелочными индикаторами. В качестве нормирующего значения X_N обычно используется предел измерений (X_N = X_max), удвоенное значение предела измерений (если нулевая отметка находится в середине шкалы), или длина шкалы (для приборов с неравномерной шкалой). Если X_N = X_max, то значение приведенной погрешности γ равно пределу допускаемой относительной погрешности средства измерений в точке, соответствующей пределу измерений. По заданному значению предела допускаемой основной приведенной погрешности легко определить предел допускаемой основной абсолютной погрешности для каждого предела измерений многопредельного прибора: .

После этого для любой отметки шкалы X может быть произведена оценка предельно-допустимой основной относительной погрешности:

.

 

Б) Нормирование пределов допускаемой основной погрешности для

средств измерений с преобладающей мультипликативной

погрешностью.

Как видно из рис.2 (2-й график), для средств измерений с преобладающей мультипликативной погрешностью, одним числом удобно нормировать предел допускаемой основной относительной погрешности (рис.2в) δ_max= ± b∙100%. В этом случае, фактическая относительная погрешность каждого экземпляра средства измерений данного типа на различных участках шкалы может иметь различные значения, но не должна превышать предельно допустимой величины (δ ≤ ± b∙100%). По заданному значению предельно допустимой относительной погрешности δ_max для любой точки шкалы может быть произведена оценка предельно-допустимой абсолютной погрешности:

.

К числу средств измерений с преобладающей мультипликативной погрешностью относится большинство многозначных мер, счетчики электрической энергии, счетчики воды, расходомеры и др. Следует отметить, что для реальных средств измерений с преобладающей мультипликативной погрешностью не удается полностью устранить аддитивную погрешность. По этой причине в технической документации всегда указывается наименьшее значение измеряемой величины, для которого предел допускаемой основной относительной погрешности ещё не превышает заданного значения δ_max. Ниже этого наименьшего значения измеряемой величины погрешность измерений не нормируется и является неопределенной.

 

В) Нормирование пределов допускаемой основной погрешности для

средств измерений с соизмеримой аддитивной и мультипликативной

погрешностью.

 

Если аддитивная и мультипликативная составляющая погрешности средства измерений соизмеримы (3-й график на рис.2), то задание предельно-допустимой погрешности одним числом не представляется возможным. В этом случае либо нормируется предел допускаемой абсолютной основной погрешности (указываются предельно-допустимые значения a и b), либо (чаще всего) нормируется предел допускаемой относительной основной погрешности. В последнем случае численные значения предельно-допустимых относительных погрешностей в различных точках шкалы оцениваются по формуле:

,

где X_max – предел измерений;

X - измеренное значение;

d = - значение приведенной к пределу измерений

аддитивной составляющей основной погрешности;

с = - значение результирующей относительной

основной погрешности в точке, соответствующей пределу

измерений.

 

Рассмотренным выше способом (указанием численных значений c и d) нормируются, в частности, предельно-допустимые значения относительной основной погрешности цифровых измерительных приборов. В этом случае относительные погрешности каждого экземпляра средств измерений определенного типа не должны превышать установленных для этого типа средств измерений значений предельно-допустимой погрешности:

.

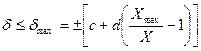При этом абсолютная основная погрешность определяется по формуле

.

 

Г) Нормирование дополнительных погрешностей.

Наиболее часто пределы допускаемых дополнительных погрешностей указывают в технической документации либо одним значением для всей рабочей области величины, влияющей на точность средства измерений (иногда несколькими значениями для поддиапазонов рабочей области влияющей величины), либо отношением предела допускаемой дополнительной погрешности к интервалу значений влияющей величины. Пределы допускаемых дополнительных погрешностей указываются на каждой, влияющей на точность средства измерений величине. При этом, как правило, значения дополнительных погрешностей устанавливают в виде дольного или кратного значения предела допускаемой основной погрешности. Например, в документации может быть указано, что при температуре окружающей среды за пределами нормальной области температур, предел допускаемой дополнительной погрешности, возникающей по этой причине, не должен превышать 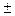0,2% на 10^о С.

 

Классы точности средств измерений.

 

Исторически по точности средства измерений подразделяют на классы. Иногда их называют классами точности, иногда классами допуска, иногда просто классами.