Числовые вероятностные характеристики погрешностей определяются при бесконечном числе опытов. В практике измерений n всегда конечно, поэтому пользуются статистическими числовыми характеристиками, которые называют оценками характеристик. Чтобы подчеркнуть различие между формулами вероятностных характеристик и их оценок, последние отмечают знаком " ˜ ".
Для решения многих задач не требуется знания функции и плотности распределения вероятностей, а вполне достаточными характеристиками случайных погрешностей служат их простейшие числовые характеристики: математическое ожидание m (истинное значение) и среднеквадратическое отклонение (дисперсия), характеризующее точность измерений. Если же известно, что распределение погрешностей гауссовское, то эти величины являются исчерпывающими характеристиками.
Рассмотрим алгоритм статистической обработки результатов измерений некоторой физической величины (например, напряжения, тока, сопротивления и т.д.).
Производят n однократных равноточных измерений в результате которых получают ряд случайных значений х1, х2,…, хi,.., хn. Требуется определить, в каких пределах находится истинное значение измеряемой величины.
1. За оценку математического ожидания (истинного значения) принимают среднее арифметическое значение:
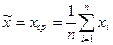
2. Оценка среднеквадратического отклонения абсолютных отклонений каждого из 
измерений определяется по формуле:
,
где 
- абсолютное отклонение (погрешность) отдельного i-го измерения.
Для того, чтобы убедиться в отсутствии промахов, используем "закон 3σ1". Выбрав из n значений Δi наибольшее, проверим выполнение соотношения (2). Если соотношение не выполняется, то результат(ы) измерения, соответствующий выбранной Δi исключается и повторяются п.п.1,2.
3. Погрешность усредненного результата n измерений будет ниже, т.к. часть погрешностей Δi взаимоуничтожится. Она характеризуется оценкой 
среднеквадратического отклонения среднего арифметического значения
.
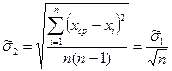4. Задавшись доверительной вероятностью Р, определим доверительный интервал, в пределах которого находится истинное значение измеряемой величины. Для нормального закона распределения доверительный интервал по заданной доверительной вероятности (и наоборот) определяется при помощи таблицы интеграла вероятности Ф(Z)=Р. Границы доверительного интервала можно вычислить по формуле In = хср ±Δ = хср ± z .
Таким способом вычисляется доверительный интервал лишь тогда, когда имеется априорная информация о гауссовском характере распределения результатов измерения. При малом числе измерений n≤ 15 доверительный интервал определяется не через 
, а через tnα – параметр распределения Стьюдента. Это распределение зависит только от числа измерений n, но не от значений хср и 
.
Задавшись доверительной вероятностью α и зная n по таблицам можно определить коэффициент 
. Далее по коэффициенту и по величине можно определить ширину доверительного интервала Δ:
.
Границы доверительного интервала определяются по формуле In = хср ±Δ = хср ± .
Из сравнения двух вариантов определения доверительного интервала видно, что при малом количестве измерений распределение Стьюдента несколько расширяет интервал, в пределах которого может находиться истинное значение величины х. При n=15 и более, величины доверительных интервалов сравниваются и вычисления можно проводить любым способом.
Суммирование погрешностей
Очень часто стоит задача определения суммарной погрешности прибора, состоящего из нескольких блоков.
 |
Рассмотрим самый общий случай, когда каждый из блоков обладает как систематической, так и случайной погрешностью.
1. Систематические погрешности суммируются алгебраически с учётом их знаков, при этом суммарная погрешность является модулем полученной суммы:
2. Случайная погрешность измерительного устройства, состоящего из 
блоков с независимыми случайными погрешностями каждого блока 
, находится путём геометрического сложения:
.
3. При наличии случайных и систематических погрешностей общая погрешность измерения находится как их геометрическая сумма:
Допускается исключение из рассмотрения так называемой ничтожной погрешности, которой называется слагаемое (слагаемые) со значением, меньшим 30% суммарной погрешности.
