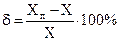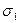Погрешности электроизмерительных приборов

 

По способу выражения в измерительных приборах различают абсолютную, относительную и приведённую погрешности. Первые две погрешности аналогичны рассмотренным выше:

- абсолютная погрешность прибора Δ=Х_п –Х. Здесь - показание прибора, Х- истинное значение измеряемой величины;

- относительная погрешность определяется как.

 

Поскольку часто истинное значение неизвестно, то часто используют более удобную запись:

 

 

- приведённая погрешность - есть выраженное в процентах отношение абсолютной погрешности к нормирующему значению L (выбор L регламентируется ГОСТ 13600-68):

.

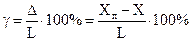Для приборов с нулевой отметкой на краю или вне шкалы нормирующее значение L равно конечному значению диапазона измерений Х_к. Если нулевая отметка находится посредине шкалы, то L равно арифметической сумме конечных значений шкалы без учёта знака.

У реальных приборов зависимость абсолютной погрешности от измеряемой величены Х может быть представлена некоторой полосой неопределённости. Эта полоса обусловлена случайной погрешностью и изменением характеристик приборов в результате действия влияющих величин и процессов старения.

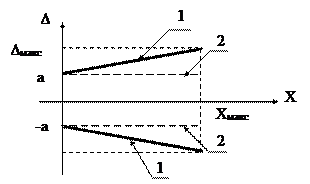Поэтому значение абсолютной погрешности, ограничивают двумя прямыми, симметричными относительно оси абсцисс, расстояние между которыми увеличивается с ростом измеряемой величины Х.

 

 

Рис.2

Уравнение прямой 1 можно записать в виде:

,

где а – предельное значение аддитивной погрешности, bx – предельное значение мультипликативной погрешности.

Абсолютные значения аддитивной погрешности не зависят от измеряемой величины Х, а мультипликативные прямо пропорциональны величине Х.

Источники аддитивной погрешности - это трение в опорах, неточность отсчёта, шум, наводки, вибрации. От этой погрешности зависит наименьшее значение величины, которое может быть измерено прибором. Причины мультипликативной погрешности - влияние внешних факторов и старение элементов, узлов приборов.

Предельное значение относительной погрешности прибора , связано с предельным значением абсолютной погрешности 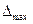зависимостью:

Согласно ГОСТ в соответствии со значением приведённой погрешности средствам измерений присваиваются классы точности.

Класс точности – это обобщённая характеристика прибора, определяемая пределами допускаемых основных и дополнительных погрешностей.

У приборов, аддитивная погрешность которых резко преобладает над мультипликативной, все значения погрешностей оказываются в пределах двух прямых параллельных оси Х (прямые 2) рис.2.

В результате допускаемая абсолютная и приведённые погрешности прибора оказываются постоянными в любой точке его шкалы. У таких приборов класс точности равен максимальному значению приведенной погрешности, выраженной в процентах и округленной до ближайшего большего значения из ряда чисел: 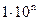; ; ; ; ; ; 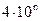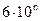, где Например, классы точности на амперметры и вольтметры, установленные ГОСТ 8711-78: 0,05; 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4,0 и 5,0.

У приборов, класс точности которых выражается одним числом, основная приведённая погрешность, выраженная в %, не превышает значения, соответствующего класса точности.

Класс точности приборов, у которых аддитивная и мультипликативная составляющие основной погрешности соизмеримы, обозначается в виде двух чисел разделённых косой чертой, например 0,1/0,05. К приборам, класс точности которых выражается дробью относятся цифровые приборы, мосты сравнения и т.д.

Предельное значение основной относительной погрешности прибора, выраженное в процентах, в этом случае может быть определено по формуле:

,% или ,% (1)

Здесь А_к - конечное значение диапазона измерений (предел измерений), А_х- измеренное значение.

 

Случайные погрешности

 

Случайные погрешности – это погрешности, изменяющиеся случайным образом при повторных измерениях одной и той же величины. Их нельзя исключить опытным путём, т.к. они происходят от одновременного влияния на результат измерения ряда величин случайного характера (внешних воздействий). Кроме этого, в случайную погрешность входят и случайные погрешности средств измерений.

Уменьшение влияния случайных погрешностей на результат измерений достигается путём усреднения многократных измерений величины в одинаковых условиях.

Рис.3

σ2 › σ1

Из теории вероятностей известно, что наиболее полно случайные величины описываются законами распределения вероятностей. В практике электрических измерений одним из наиболее распространённых законов является нормальный закон (распределение Гаусса).

 

 

 

 

 

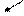
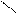
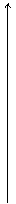
Функция распределения для нормального закона (рис.3) выражается зависимостью

где - функция распределения плотности вероятности случайной погрешности ,

σ- среднеквадратическое отклонение,

D=σ² – дисперсия, характеризующая рассеивание случайной погрешности относительно центра распределения.

График показывает, что чем меньше σ, тем чаще встречаются погрешности малой величины (тем точнее выполнены измерения).

В общем случае вероятность появления погрешности со значением от до определяется площадью заштрихованного участка на рис.3 и может быть вычислена по формуле:

.

Следует учесть, что эта функция нормирована, т.е.

,

поэтому кривые σ₁ и σ₂ всегда имеют форму, обеспечивающую равенство 1 площадей под этими кривыми.

Интервал от до называется доверительным, а соответствующая вероятность – доверительной вероятностью. Следовательно, доверительный интервал - это интервал, в пределах которого находится искомая величина с вероятностью, называемой доверительной.

Если ввести нормированную случайную величину , то правая часть преобразуется в функцию Лапласа, часто называемую интегралом вероятности:

.

Он табулирован и его график представлен на рис.4:

 

Если задана некоторая вероятность 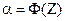, то найдя можно определить погрешность по формуле . Эта погрешность и будет определять величину доверительного интервала.

Табулированные значения функции 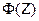показывают, что вероятность появления погрешности Δ в интервале от 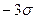до составляет 0,9973. Вероятность появления погрешности большей чем ± равна (1 - 0,9973) = 0,0027 ≈ 1/370. Это означает, что только одна из 370 погрешностей (т.е. примерно 0,3% их числа) будет больше по абсолютному значению .

Погрешность ± принимают за максимальную погрешность. Погрешности больше , считаются промахами и при обработке результатов измерений не учитываются (отбрасываются). Часто это условие называют "законом 3σ", т.е. если выполняется условие

Δ_{i max} ≤ 3σ, (2)

то считается, что в этом случае в результатах измерений промахов нет (с вероятностью 0,3%).