Маршрутом в графе G называется чередующаяся последовательность вершин и ребер: v0, l 1, v1, l 2,…, lk, vk, в которой любые два соседних элемента инцидентны. Это определение подходит и для псевдо и мультиграфов. В орграфе достаточно указать только последовательность вершин (узлов) или только последовательность ребер (дуг) если v0=vk,то маршрут называется замкнутым, если нет, то открытым.
Если все ребра различны, то маршрут называется цепью, если все вершины различны, то маршрут называется простой цепью В цепи v0 и vk называются концами цепи; цепь соединяющая вершины u и v обозначают < u, v>; замкнутая цепь называется циклом; простая замкнутая цепь прстым циклом. Граф без циклов называется ациклическим.
Для орграфов цепь называется путем, а цикл – контуром.
Пример 1.
v1 v2
1º v1, v3, v1, v4 – маршрут, но не цепь.
2º v1, v3, v5, v2, v3, v4 – цепь, но не простая (т.к. не все
v3 вершины различны, а различны рёбра)
3º v1, v4, v3, v2, v5 – простая цепь, но не цикл (т.к. не
v4v5 замкнута)
4º v1, v3, v5, v2, v3, v4, v1 – но не простой (т.к. цепь не простая хотя, замкнутая)
5º v1, v3, v4, v1 – простой цикл (все ребра и все вершины различны)
Длиной маршрута называется количество ребер в нем (с повторениями).
Пример 2.
Дан граф G, в нем:
1 2 (1,2), (1,2,4,7), (3,4,5,6) – простые цепи
(3,4,5,6) – цепь простая, но не ЦИК
3 4 5 6
(1,2,4,7,8,4) – не простая цепь (есть одинаковые
вершины)
7 8 (1,2,4,7,8,4,1) – цикл, но не простой.
Пусть G – граф, возможно ориентированный. Маршрут называется путём, если все его дуги различны. Путь называется контуром, если v0=vk. Вершина v называется достижимой из вершины u, если 
<u, v> путь. Расстоянием между вершинами называется длина кратчайшей цепи <u, v>
Пример 3.
2 4 5
1 3
Контур (1,2,3)
Вершина 5 достижима из любой вершины; из вершины 5 недостижима ни одна из остальных вершин
Матрица инциденций вершин и ребер
Представление графа с помощью матрицы, отражающей инцидентность вершин и ребер называется матрицей инциденций.
Для неографа:
М 
= 
Для ориентированного графа:
H = 
Пример 1. (Неограф)
v1 L1 v2
G: L4 L5 L2
v4 L3 v3
G: 
- матрица инциденций вершин и ребер для графа G
Пример 2.(Орграф)
V1 L1 V2
D: L4 L5 L2
V4 L3 V3
D: 
- матрица смежности вершин и ребер в орграфе
Матрица смежности вершин
Матрица инциденций вершин отражает смежность вершин.
Пример 1.
а1 а2
G: а5
а3 а4
AG=(Ai, j) = 
; AG= 
Для мультиграфа G матрица инцидентности дуг и вершин
BG=(Bi, j) = 
Это – матрица размера m×n, I = 1,2…,m
J = 1,2,…,n
Пример 2.
a2 4 a3
3
1 2
a1
BG= 
m×n3×6 
Тема: Комбинаторика
1. Размещения из n элементов по m это - упорядоченные подмножества из n элементов по m.
Число размещений 
(n-факториал)
2. Перестановки - размещение и n элементов по n т.е. частный случай размещений число перестановок Pn=n!
3. Сочетания – подмножество из п элементов по m, отличающихся друг от друга хотя бы одним элементом называются сочетаниями. Число сочетаний 
Пример:
1. Сколькими способами можно расположить 5 различных книг на полке? Р5=1*2*3*4*5=120 способов.
2. Сколько способов распределить 3 различных путевки среди 8 человек бригады?
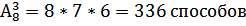
3. Сколько способов распределить 3 одинаковых обязанностей в группе из 25 человек?
способов т.к. обязанности одинаковы – это сочетания
