Результаты наблюдений, полученные при наличии систематических погрешностей, будем называть неисправленными и в отличие от исправленных снабжать штрихами их обозначения (например 
и т.д.). Вычисленные в этих условиях средние арифметические значения и отклонения от результатов наблюдений будем также называть неисправленными и ставить штрихи у символов этих величин. Таким образом,
 .
| (58) |
Поскольку неисправленные результаты наблюдений включают в себя систематические погрешности, сумму которых для каждого 
-го наблюдения будем обозначать через 
, то их математическое ожидание не совпадает с истинным значением измеряемой величины и отличается от него на некоторую величину 
, называемую систематической погрешностью неисправленного среднего арифметического. Действительно,
.
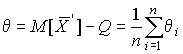Если систематические погрешности постоянны, т.е. 
то неисправленные отклонения могут быть непосредственно использованы для оценки рассеивания ряда наблюдений. В противном случае необходимо предварительно исправить отдельные результаты измерений, введя в них так называемые поправки, равные систематическим погрешностям по величине и обратные им по знаку:
.
Таким образом, для нахождения исправленного среднего арифметического и оценки его рассеивания относительно истинного значения измеряемой величины необходимо обнаружить систематические погрешности и исключить их путем введения поправок или соответствующей каждому конкретному случаю организации самoгo измерения. Остановимся подробнее на некоторых способах обнаружения систематических погрешностей.
Постоянные систематические погрешности не влияют на значения случайных отклонений результатов наблюдений от средних арифметических, поэтому никакая математическая обработка результатов наблюдений не может привести к их обнаружению. Анализ таких погрешностей возможен только на основании некоторых априорных знаний об этих погрешностях, получаемых, например, при поверке средств измерений. Измеряемая величина при поверке обычно воспроизводится образцовой мерой, действительное значение которой известно. Поэтому разность между средним арифметическим результатов наблюдения и значением меры с точностью, определяемой погрешностью аттестации меры и случайными погрешностями измерения, равна искомой систематической погрешности.
Ценность полученных при поверке результатов определяется их постоянством в течение некоторого промежутка времени и независимостью от тех изменений внешних условий, которые допустимы при эксплуатации средств измерений с заданной точностью. Тогда полученные при поверке данные могут быть использованы для вычисления поправок, необходимых для исправления результатов наблюдений.
Одним из наиболее действенных способов обнаружения систематических погрешностей в ряде результатов наблюдений является построение графика последовательности неисправленных значений случайных отклонений результатов наблюдений от средних арифметических.
Вначале рассмотрим случай, когда в ряде результатов наблюдений предполагается наличие постоянной систематической погрешности. Для того чтобы удостовериться в этом, исследователь, сделав несколько измерений, заменяет некоторые меры или измерительные приборы, включенные в установку и являющиеся предполагаемыми источниками постоянных систематических погрешностей, другими мерами и измерительными приборами и проводит еще несколько измерений.
Рассматриваемый способ обнаружения постоянных систематических погрешностей можно сформулировать следующим образом: если неисправленные отклонения результатов наблюдений резко изменяются при изменении условий наблюдений, то данные результаты содержат постоянную систематическую погрешность, зависящую от условий наблюдений.
При прогрессивной систематической погрешности последовательность неисправленных отклонений результатов наблюдений обнаруживает тенденцию к возрастанию или убыванию. На рис.13 изображена зависимость погрешности измерения от длины измеряемой детали.
Несмотря на большие случайные изменения погрешности тенденция к увеличению ее в отрицательном направлении с ростом измеряемой величины явно обнаруживается. Если бы случайные погрешности были невелики, то значения неисправленных отклонений меняли бы свой знак при некотором среднем значении измеряемой величины. Случайные погрешности несколько искажают эту картину, однако, если они даже одного порядка малости с систематическими погрешностями, в последовательности знаков можно заметить некоторую неравномерность: неисправленные отклонения результатов одного знака чаще встречаются в отрицательной полуплоскости, чем в положительной.
Если же в ряде результатов наблюдений присутствует периодическая систематическая погрешность, то группы знаков плюс и минус в последовательности неисправленных отклонений результатов наблюдений могут периодически сменять друг друга, если, конечно, случайные погрешности не особенно велики.
Обобщая два рассмотренных случая, можно сказать: если последовательность знаков плюс сменяется последовательностью знаков минус или наоборот, то данный ряд результатов наблюдений обнаруживает прогрессивную погрешность, если группы знаков плюс и минус чередуются - периодическую погрешность.
Введение поправок. Неисключенная систематическая погрешность
Систематические погрешности являются детерминированными величинами, поэтому в принципе всегда могут быть вычислены и исключены из результатов измерений. После исключения систематических погрешностей получаем исправленные средние арифметические и исправленные отклонения результатов наблюдении, которые позволяют оценить степень рассеивания результатов.
Для исправления результатов наблюдений их складывают с поправками, равными систематическим погрешностям по величине и обратными им по знаку. Поправку определяют экспериментально при поверке приборов или в результате специальных исследований, обыкновенно с некоторой ограниченной точностью. Для исправления результата наблюдения его складывают только со средним арифметическим значением поправки:
 ,
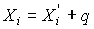| (59) |
где 
и 
– соответственно исправленный и неисправленный результаты наблюдений, 
– среднее арифметическое значение поправки, определяемые экспериментально.
Поправки могут задаваться также в виде формул, по которым они вычисляются для каждого конкретного случая. Например, при измерениях и поверках с помощью образцовых манометров следует вводить поправки к их показаниям на местное значение ускорения свободного падения
,
где 
– измеряемое давление.
Введением поправки устраняется влияние только одной вполне определенной систематической погрешности, поэтому в результаты измерения зачастую приходится вводить очень большое число поправок. При этом вследствие ограниченной точности определения поправок накапливаются случайные погрешности и дисперсия результата измерения увеличивается.
Действительно, при исправлении неисправленного результата путем введения поправок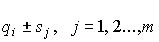 
по формуле
 ,
| (60) |
дисперсия 
становится равной
 ,
| (61) |
где – оценка дисперсии неисправленных результатов; 
– оценка дисперсии 
-й поправки.
Поправку имеет смысл вводить до тех пор, пока она уменьшает доверительные границы погрешности, т.е. пока выполняется неравенство
 .
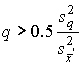| (62) |
При малой дисперсии поправки на основании формулы (62) может показаться, что введение любой поправки повышает достоверность результата. Однако следует помнить, что погрешность результата выражается не более чем двумя значащими цифрами, поэтому поправка, если она меньше пяти единиц разряда, следующего за последним десятичным знаком погрешности результата, будет все равно потеряна при округлении, и вводить ее не имеет смысла.
Систематическая погрешность, остающаяся после введения поправок на ее наиболее существенные составляющие включает в себя ряд элементарных составляющих, называемых неисключенными остатками систематической погрешности. К их числу относятся:
- погрешности определения поправок;
- погрешности, зависящие от точности измерения влияющих величин, входящих в формулы для определения поправок;
- погрешности, связанные с колебаниями влияющих величин (температуры окружающей среды, напряжения питания и т.д.).
Перечисленные погрешности малы и поправки на них не вводятся.
Для каждого данного измерения элементарные составляющие систематической погрешности имеют вполне определенные значения, но эти значения нам неизвестны. Известно лишь, что в массе однотипных измерений эти составляющие лежат в определенных границах 
или имеют определенные средние квадратические отклонения 
. В первом случае для неисключенных остатков следует принять равномерное распределение, во втором – нормальное. Дисперсия суммы неисключенных остатков систематической погрешности определяется как сумма их дисперсий и поэтому
 ,
| (63) |
где m1 – число равномерно распределенных и m2 – число нормально распределенных элементарных составляющих.
