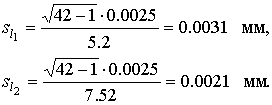—мысл оценки параметров с помощью интервалов заключаетс€ в нахождении интервалов, называемых доверительными, между границами которых с определенными веро€тност€ми (доверительными) наход€тс€ истинные значени€ оцениваемых параметров.
¬начале остановимс€ на определении доверительного интервала дл€ среднего арифметического значени€ измер€емой величины. ѕредположим, что распределение результатов наблюдений нормально и известна дисперси€  . Ќайдем веро€тность попадани€ результата наблюдений в интервал
. Ќайдем веро€тность попадани€ результата наблюдений в интервал  . —огласно формуле (29)
. —огласно формуле (29)

Ќо

и, если систематические погрешности исключены 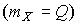 ,
,
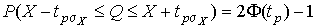
| (34) |
Ёто означает, что истинное значение Q измер€емой величины с доверительной веро€тностью 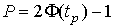 находитс€ между границами доверительного интервала
находитс€ между границами доверительного интервала 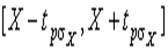 .
.
ѕоловина длины доверительного интервала 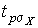 называетс€ доверительной границей случайного отклонени€ результатов наблюдений, соответствующей доверительной веро€тности –. ƒл€ определени€ доверительной границы (при выполнении перечисленных условий) задаютс€ доверительной веро€тностью, например – =0.95 или – =0.995 и по формулам
называетс€ доверительной границей случайного отклонени€ результатов наблюдений, соответствующей доверительной веро€тности –. ƒл€ определени€ доверительной границы (при выполнении перечисленных условий) задаютс€ доверительной веро€тностью, например – =0.95 или – =0.995 и по формулам
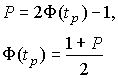
| (35) |
определ€ют соответствующее значение 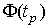 интегральной функции нормированного нормального распределени€. «атем по данным табл.ѕ.3 приложени€ наход€т значение коэффициента
интегральной функции нормированного нормального распределени€. «атем по данным табл.ѕ.3 приложени€ наход€т значение коэффициента  и вычисл€ют доверительное отклонение
и вычисл€ют доверительное отклонение 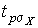 . ѕроведение многократных наблюдений позвол€ет значительно сократить доверительный интервал. ƒействительно, если результаты наблюдений
. ѕроведение многократных наблюдений позвол€ет значительно сократить доверительный интервал. ƒействительно, если результаты наблюдений  (i =l, 2,..., n) распределены нормально, то нормально распределены и величины
(i =l, 2,..., n) распределены нормально, то нормально распределены и величины  , а значит, и среднее арифметическое
, а значит, и среднее арифметическое 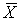 , €вл€ющеес€ их суммой. ѕоэтому имеет место равенство
, €вл€ющеес€ их суммой. ѕоэтому имеет место равенство

| (36) |
где 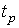 определ€етс€ по заданной доверительной веро€тности –.
определ€етс€ по заданной доверительной веро€тности –.
ѕолученный доверительный интервал, построенный с помощью среднего арифметического результатов n независимых повторных наблюдений, в  раз короче интервала, вычисленного по результату одного наблюдени€, хот€ доверительна€ веро€тность дл€ них одинакова. Ёто говорит о том, что сходимость измерений растет пропорционально корню квадратному из числа наблюдений.
раз короче интервала, вычисленного по результату одного наблюдени€, хот€ доверительна€ веро€тность дл€ них одинакова. Ёто говорит о том, что сходимость измерений растет пропорционально корню квадратному из числа наблюдений.
ѕоловина длины нового доверительного интервала

| (37) |
называетс€ доверительной границей погрешности результата измерений, а итог измерений записываетс€ в виде
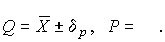
| (38) |
“еперь рассмотрим случай, когда распределение результатов наблюдений нормально, но их дисперси€ неизвестна. ¬ этих услови€х пользуютс€ отношением

| (39) |
называемым дробью —тьюдента. ¬ход€щие в нее величины 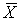 и
и 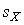 вычисл€ют на основании опытных данных; они представл€ют собой точечные оценки математического ожидани€ и среднеквадратического отклонени€ результатов наблюдений.
вычисл€ют на основании опытных данных; они представл€ют собой точечные оценки математического ожидани€ и среднеквадратического отклонени€ результатов наблюдений.
ѕлотность распределени€ этой дроби, впервые предсказанного √оссетом, писавшим под псевдонимом —тьюдент, выражаетс€ следующим уравнением:
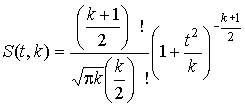
| (40) |
где S (t, k) - плотность распределени€ —тьюдента. ¬еличина k называетс€ числом степеней свободы и равна n - 1. ¬еро€тность того, что дробь —тьюдента в результате выполненных наблюдений примет некоторое значение в интервале  , согласно выражению (8), вычисл€етс€ по формуле
, согласно выражению (8), вычисл€етс€ по формуле
|
|
|
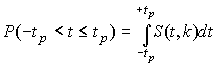
или, поскольку S (t, k) €вл€етс€ четной функцией аргумента t,
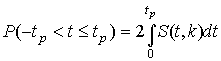
ѕодставив вместо дроби —тьюдента t ее выражение через  и
и  , получим окончательно
, получим окончательно
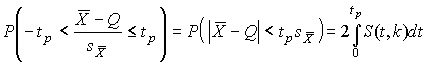 . .
| (41) |
¬еличины  , вычисленные по формулам (40) и (41), были табулированы ‘ишером дл€ различных значений доверительной веро€тности – в пределах 0.10 - 0.99 при
, вычисленные по формулам (40) и (41), были табулированы ‘ишером дл€ различных значений доверительной веро€тности – в пределах 0.10 - 0.99 при  ¬ табл.ѕ.5 приведены значени€
¬ табл.ѕ.5 приведены значени€ 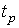 дл€ наиболее часто употребл€емых доверительных веро€тностей –.
дл€ наиболее часто употребл€емых доверительных веро€тностей –.
“аким образом, с помощью распределени€ —тьюдента по формуле (41) может быть найдена веро€тность того, что отклонение среднего арифметического от истинного значени€ измер€емой величины не превышает 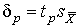 , например
, например 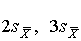 и т.д. »тог измерений записываетс€ в виде
и т.д. »тог измерений записываетс€ в виде

| (42) |
ѕример. ѕо результатам п€ти наблюдений была найдена длина стержн€. »тог измерений составл€ет L =15.785 мм, 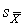 =0.005 мм, причем существуют достаточно обоснованные предположени€ о том, что распределение результатов наблюдений было нормальным. “ребуетс€ оценить веро€тность того, что истинное значение длины стержн€ отличаетс€ от среднего арифметического из п€ти наблюдений не больше чем на 0.01 мм.
=0.005 мм, причем существуют достаточно обоснованные предположени€ о том, что распределение результатов наблюдений было нормальным. “ребуетс€ оценить веро€тность того, что истинное значение длины стержн€ отличаетс€ от среднего арифметического из п€ти наблюдений не больше чем на 0.01 мм.
»з услови€ задачи следует, что имеютс€ все основани€ дл€ применени€ распределени€ —тьюдента.
¬ычисл€ем значение дроби —тьюдента
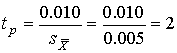
и число степеней свободы

.
ѕо данным табл.ѕ.4 приложени€ находим значение доверительной веро€тности дл€
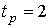 и
и 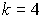 :
: 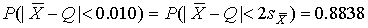 .
.
ƒл€ 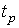 =3 веро€тность составл€ет
=3 веро€тность составл€ет
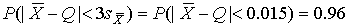
т.е несколько меньше 0.9973, как при нормальном распределении. »тог измерений удобно записать в виде
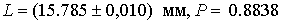 .
.
ƒл€ 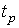 =1 доверительна€ веро€тность составл€ет приблизительно 0.62, поэтому итог измерений можно представить также в виде
=1 доверительна€ веро€тность составл€ет приблизительно 0.62, поэтому итог измерений можно представить также в виде
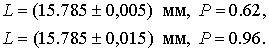
ѕример. ¬ услови€х предыдущей задачи найти доверительную границу погрешности результата измерений дл€ доверительной веро€тности  . ѕо данным табл.ѕ.5 при
. ѕо данным табл.ѕ.5 при 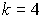 находим
находим 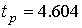 и, следовательно, доверительна€ граница:
и, следовательно, доверительна€ граница:
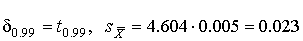 мм.
мм.
»тог измерений:
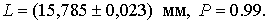
ѕри  , а практически уже при
, а практически уже при 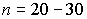 распределение —тьюдента переходит в нормальное распределение и
распределение —тьюдента переходит в нормальное распределение и
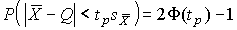
где 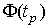 - интегральна€ функции нормированного нормального распределени€.
- интегральна€ функции нормированного нормального распределени€.
¬ тех случа€х, когда распределение случайных погрешностей не €вл€етс€ нормальным, все же часто пользуютс€ распределением —тьюдента с приближением, степень которого остаетс€ неизвестной.
роме того, на основании центральной предельной теоремы теории веро€тностей можно утверждать, что при достаточно большом числе наблюдений распределение среднего арифметического как суммы случайных величин  будет сколь угодно близким к нормальному. “огда, замен€€ дисперсию
будет сколь угодно близким к нормальному. “огда, замен€€ дисперсию  ее точечной оцен-кой [см.п.4.4. Ќормальное распределение], можно дл€ оценки доверительной гра-ницы погрешности результата воспользоватьс€ равенством (35). „исло наблюдений n, при котором это становитс€ возможным, зависит, конечно, от распределени€ случайных погрешностей.
ее точечной оцен-кой [см.п.4.4. Ќормальное распределение], можно дл€ оценки доверительной гра-ницы погрешности результата воспользоватьс€ равенством (35). „исло наблюдений n, при котором это становитс€ возможным, зависит, конечно, от распределени€ случайных погрешностей.
—оотношени€ (38) показывают, что итог измерени€ не есть одно определенное число. ¬ результате измерений мы получаем лишь полосу значений измер€емой величины. —мысл итога измерений, например, L =20.00±0.05 заключаетс€ не в том, что L = 20.00, как дл€ простоты счи-тают, а в том, что истинное значение лежит где-то в границах от 19.95 до 20.05. тому же нахождение внутри границ имеет некоторую веро€тность, меньшую, чем единица, и, следовательно, нахождение вне границ не исключено, хот€ и может быть очень маловеро€тным.
“еперь найдем доверительные интервалы дл€ дисперсии и среднеквадратического отклонени€ результатов наблюдений.
|
|
|
≈сли распределение результатов наблюдений нормально, то отношение
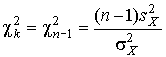
| (43) |
имеет так называемое  -распределение ѕирсона с
-распределение ѕирсона с 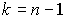 степен€ми свободы. ≈го дифференциальна€ функци€ распределени€ описываетс€ формулой
степен€ми свободы. ≈го дифференциальна€ функци€ распределени€ описываетс€ формулой

| (44) |
ривые плотности 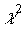 -распределени€ при различных значени€х k, вычисленные по формуле (44), представлены на рис.9.
-распределени€ при различных значени€х k, вычисленные по формуле (44), представлены на рис.9.

«начени€ 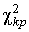 , соответствующие различным веро€тност€м – того, что отношение (43) в данном опыте будет меньше
, соответствующие различным веро€тност€м – того, что отношение (43) в данном опыте будет меньше 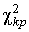 , представлены в табл.ѕ.6 приложени€ дл€ различных веро€тностей – и чисел k степеней свободы.
, представлены в табл.ѕ.6 приложени€ дл€ различных веро€тностей – и чисел k степеней свободы.
ѕользу€сь этой таблицей, можно найти доверительный интервал дл€ оценки дисперсии результатов наблюдений при заданной доверительной веро€тности. Ётот интервал строитс€ таким образом, чтобы веро€тность выхода дисперсии за его границы не превышала некоторой малой величины q, причем веро€тности выхода за обе границы интервала были бы равны между собой и составл€ли соответственно q /2 (рис.10).
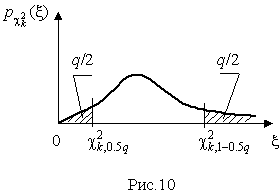
√раницы 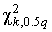 и
и  такого доверительного интервала наход€т из равенства
такого доверительного интервала наход€т из равенства

| (45) |
“еперь, зна€ границы доверительного интервала дл€ отношени€ 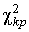 , запишем доверительный интервал дл€ дисперсии:
, запишем доверительный интервал дл€ дисперсии:
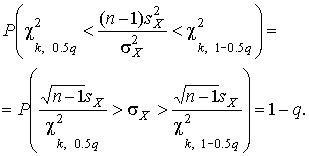
| (46) |
ѕолученное равенство означает, что с веро€тностью 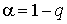 истинное значение
истинное значение  среднеквадратического отклонени€ результатов наблюдений лежит в интервале (
среднеквадратического отклонени€ результатов наблюдений лежит в интервале ( ], границы которого равны
], границы которого равны
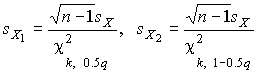
| (47) |
ѕример. ƒаны результаты двадцати измерений длины 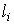 мм детали (табл.3).
мм детали (табл.3).
“аблица 3
| 18.305 | 18.306 | 18.306 | 18.309 |
| 18.308 | 18.309 | 18.313 | 18.308 |
| 18.312 | 18.310 | 18.305 | 18.307 |
| 18.309 | 18.303 | 18.307 | 18.309 |
| 18.304 | 18.308 | 18.308 | 18.310 |
¬ качестве оценки математического ожидани€ длины детали принимаем ее среднее арифметическое
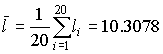 мм.
мм.
“очечна€ оценка среднеквадратического отклонени€ результатов наблюдений составл€ет:
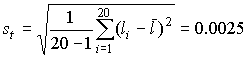 мм.
мм.
ѕрин€в уровень доверительной веро€тности 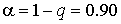 , находим дл€ числа степеней свободы
, находим дл€ числа степеней свободы 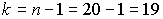 в табл.ѕ.6 приложени€:
в табл.ѕ.6 приложени€:

√раницы доверительного интервала дл€ среднеквадратического отклонени€ результатов наблюдений находим по формуле (47):

ѕолученные результаты говор€т о том, что истинное значение среднеквадратического отклонени€ результатов наблюдений с веро€тностью 0.90 лежит в интервале 0.0020 - 0.0034 мм.
¬ табл.ѕ.6 приведены значени€ 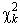 только при числах степеней свободы от 1 до 30. ѕри k >30 можно пользоватьс€ приближенной формулой
только при числах степеней свободы от 1 до 30. ѕри k >30 можно пользоватьс€ приближенной формулой

где 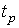 определ€етс€ из услови€
определ€етс€ из услови€ 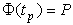 по табл.ѕ.3, в которой помещены значени€ интегральной функции нормированного нормального распределени€.
по табл.ѕ.3, в которой помещены значени€ интегральной функции нормированного нормального распределени€.
“огда границы доверительного интервала дл€ среднеквадратического отклонени€ результатов наблюдений при доверительной веро€тности 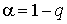 вычисл€ютс€ по формулам (47) при значени€х
вычисл€ютс€ по формулам (47) при значени€х 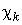 , равных
, равных

| (49) |
“ак, если в услови€х предыдущей задачи среднеквадратическое отклонение определено на основании 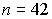 измерений, то дл€
измерений, то дл€ 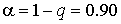 из табл.ѕ.3 находим:
из табл.ѕ.3 находим:
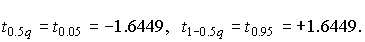
¬еличины 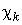 при
при 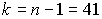 составл€ют:
составл€ют:
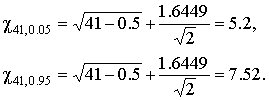
√раницы доверительного интервала: