Если случайная величина есть сумма большого числа независимых величин, то она имеет распределение, близкое к нормальному.
Пусть есть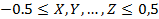 
.
Поочередно построим плотность вероятности для S(x)=X; S(x,y)=X+Y. Увидим приближение к нормальному закону. Хорошая нормализация достигается уже при 5 величинах.
Показатели среднего.
Среднее арифметическое 
, Мода 
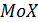(наиболее часто встречающееся), Медиана 
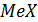(середина упорядоченного ряда значений)
Показатели вариации.
Размах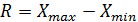 
; Выборочная дисперсия 
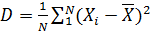; Выборочное среднее квадратическое отклонение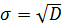 
Качество оценивания параметров.
"Хорошая" оценка обладает свойствами несмещенности(m(x)=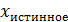 
), эффективности (малый размер D) и состоятельности (
).
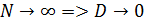Для этого используется функция максимального правдоподобия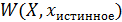 
Максимально правдоподобные оценки математического ожидания и дисперсии и их свойства.
Оптимальной оценкой мат. ожидания является ; Дисперсии - выборочная дисперсия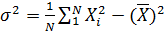 
Интервальная оценка.
Область, где лежит m(X) с вероятностью p.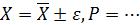 
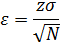
Оценка объема выборки.
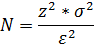
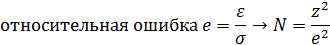
Критерии проверки гипотез.
Пусть имеется выборка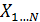 
. Известно, что она принадлежит либо к распределению W(X,v0), либо к W(X,v1).Если 
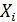независимы друг от друга, то 
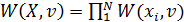. Выдвигаем 2 гипотезы, 
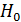и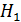 
соответственно. В ходе проверки устанавливается, в какую из полученных областей (
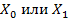) попадает исходная выборка.
Проверка гипотез о среднем значении случайной величины.
Ковариация и коэффициент корреляции совокупности двух взаимосвязанных случайных величин.
Ковариация случайных величин X и Y есть мат. ожидание произведения отклонений этих величин относительно средних.
Общие формулы:
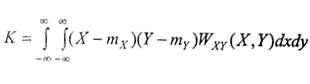
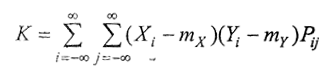
Коэффициент корреляции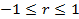 
, чем он больше, тем сильнее связь между двумя величинами. 
.
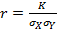Выборочные ковариация и коэффициент корреляции случайных величин.
3 типа связи (линейная, статистическая, независимость величин).
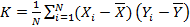
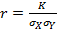
Линейное уравнение регрессии.
Линейное уравнение показывает зависимость величин со статистической связью. График уравнения строится по формуле:
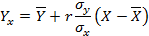
График всегда проходит через точку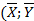 
)
Нелинейное уравнение регрессии.
Множественная линейная регрессия.
Классификация и описание случайных процессов.
Корреляционная функция случайного процесса.
Гауссовский случайный процесс
Оценка математического ожидания нестационарного случайного процесса.
Алгоритмы прогнозирования случайных процессов.
28. 
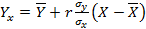
29.
