Этапы исследования статистической информации
1. Сбор и группировка данных.
2. Обработка и анализ.
Основные задачи статистики.
-Оценивание параметров распределения по полученной выборке.
-Проверка статистических гипотез; отсеивание грубых измерений, аппроксимация гистограмм аналитическими функциями, дисперсионный анализ.
-Исследование статистической зависимости двух и более случайных величин с помощью регрессионного анализа статистических значений.
-Анализ временных процессов для выявления основной тенденции случайного процесса и прогнозирования его дальнейшего развития.
Выборочная совокупность данных. Репрезентативность выборки, способы отбора статистической информации.
Выборка - случайно отобранные объекты. Выборка должна быть репрезентативной, т.е. отображать общую тенденцию большей группы. Типы отбора с.в.
-Простой (в случайном порядке N штук)
-Типический (из каждой "типичной" группы равное количество)
-Механический (из каждой N-ной случайно составленной группы по штуке)
-Серийный (из нескольких "типичных" групп исследуются лишь некоторые, но целиком)
-Комбинированный (сочетание ранее указанных способов)
Точность сбора статистической информации.
Причины, вызывающие ошибки:
- нерепрезентативная выборка по причине неверно выбранного контура статистического исследования
- Малый размер выборки (N)
- Ошибки при наблюдении исследуемого признака
Последовательность решения задачи статистической группировки.
1. Нахождение количества групп 
2....интервала 
3.Оформление результата группировки в таблицу
| № группы | Границы группы | Количество значений  в группе
| Относительная частота
| Плотность вероятностей
|
| 1...m | ... | ... | ... | ... |
| 
| 
|
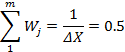
4. Гистограмма.
Сглаживание выборочной плотности вероятностей.
Для сглаживания производится аппроксимация.
Гауссовская функция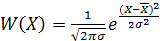 
, где
- выборочное среднее, т.е. среднее арифметическое средних арифметических каждой m-ной группы.
σ - выборочное среднее квадратическое отклонение (от средних арифметических каждой m-ной группы)
Бинарное распределение дискретной случайной величины, ее математическое ожидание, дисперсия и среднее квадратическое отклонение.
Только 2 возможных значения: 
и 
с определенной их вероятностью.
Равномерное распределение непрерывной случайной величины, ее математическое ожидание, дисперсия и среднее квадратическое отклонение.
На интервале от a до b в любой точке вероятность выпадения случайной величины равна 
.
Нормальное распределение случайной величины, ее математическое ожидание, дисперсия и среднее квадратическое отклонение.
По функции Гаусса. 
; μ - положение максимума, от его изменения зависит высота графика. Положение по X зависит от σ.
