Таблица №5 Корреляционно-регрессионный анализ
| Номер предприятия | Фондовооруженность труда, тыс.руб./чел., Х | Размер прибыли, тыс.руб. У | Х2 | ХУ |
| 35,6 | 1267,36 | 23460,4 | ||
| 25,8 | 665,64 | 75000,6 | ||
| 24,7 | 610,09 | 87289,8 | ||
| 27,3 | 745,29 | 19628,7 | ||
| 24,9 | 620,01 | 102463,5 | ||
| 19,9 | 396,01 | |||
| 18,1 | 327,61 | 185742,2 | ||
| 33,9 | 1149,21 | 33866,1 | ||
| 35,2 | 1239,04 | 88598,4 | ||
| 19,9 | 396,01 | 106425,2 | ||
| 17,2 | 295,84 | 125594,4 | ||
| 29,5 | 870,25 | 41093,5 | ||
| 30,5 | 930,25 | 54564,5 | ||
| 22,4 | 501,76 | 117062,4 | ||
| 17,5 | 306,25 | 114187,5 | ||
| 35,1 | 1232,01 | 41382,9 | ||
| 28,4 | 806,56 | 92243,2 | ||
| 15,8 | 249,64 | 126700,2 | ||
| 26,9 | 723,61 | 107949,7 | ||
| 26,3 | 691,69 | |||
| 12,9 | 166,41 | 108463,2 | ||
| 17,6 | 309,76 | 134411,2 | ||
| 23,8 | 566,44 | 160126,4 | ||
| 27,4 | 750,76 | 123656,2 | ||
| 19,6 | 384,16 | |||
| 36,6 | 1339,56 | |||
| 16,7 | 278,89 | 129992,8 | ||
| 23,2 | 538,24 | 138782,4 | ||
| 32,3 | 1043,29 | 113566,8 | ||
| Итого | 20425,6 | 2946791,2 |
Уравнение регрессии имеет вид
Yх = а0 + a1X
Система нормальных уравнений имеет вид
na0 + a1SX = SY;
a0SX + a1SX2 = SXY
30*а0+а1*757=135373
а0*757+а1*20425,60=2946791,20
Отсюда а0=13435,02, а1=-353,65
Следовательно
Yх = а0 + a1X, = 13435,02+(-353,65)*Х
Определим тесноту связи признаков с помощью коэффициента Фехнера.
Кф =(А-В)/(А+В)
Среднее значение X=757/30=25,23, Y=135373/30 = 4512,43
Таблица 6 Расчет значений коэффициента корреляции знаков Фехнера
| № п/п | Фондовооруженность труда, тыс.руб./чел., Х | Размер прибыли, тыс.руб. У | Знаки отклонений значений признака от средней | Совпадение (а) или несовпадение (в) знаков | |
| Для X | Для Y | ||||
| 35,6 | + | - | В | ||
| 25,8 | + | - | В | ||
| 24,7 | - | - | А | ||
| 27,3 | + | - | В | ||
| 24,9 | - | - | А | ||
| + | - | В | |||
| 19,9 | - | + | В | ||
| 18,1 | - | + | В | ||
| 33,9 | + | - | В | ||
| 35,2 | + | - | В | ||
| 19,9 | - | + | В | ||
| 17,2 | - | + | В | ||
| 29,5 | + | - | В | ||
| 30,5 | + | - | В | ||
| 22,4 | - | + | В | ||
| 17,5 | - | + | В | ||
| 35,1 | + | - | В | ||
| 28,4 | + | - | В | ||
| 15,8 | - | + | В | ||
| 26,9 | + | - | В | ||
| 26,3 | + | + | А | ||
| 12,9 | - | + | В | ||
| 17,6 | - | + | В | ||
| 23,8 | - | + | В | ||
| 27,4 | + | + | А | ||
| 19,6 | - | + | В | ||
| 36,6 | + | - | В | ||
| 16,7 | - | + | В | ||
| 23,2 | + | + | А | ||
| 32,3 | + | - | В |
Кф =(А-В)/(А+В) = (5-25)/(5+25) = -0,67
Это значение свидетельствует о возможном наличии обратной связи.
Часть 4. Анализ рядов динамики
4.1
Используя приведенные ниже данные из статистических публикаций (материалы сайта Росстата www.gks.ru), проведем анализ динамики экономического показателя за указанные годы.
Таблица 10. Среднемесячная номинальная заработная плата работников организаций по видам экономической деятельности (рублей)
| Вид экономической деятельности | |||||||
| Образование | 5429,7 | 6983,3 | 8778,3 | 11316,8 | 13293,6 | 14075,2 |
Это интервальный ряд динамики, так как данные представлены за период (год).
Представим ряд графически.
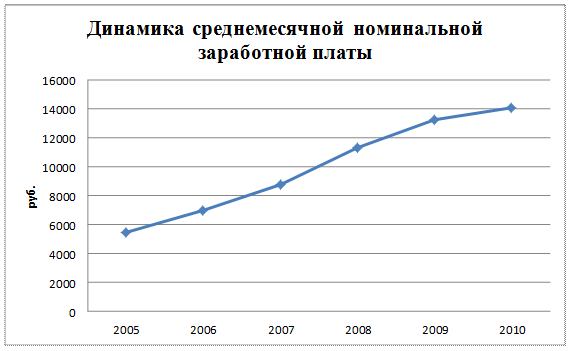
Рис. 1 Динамика среднемесячной номинальной заработной платы работников образования
В зависимости от задач исследования и способа представления данных показатели изменения динамического ряда рассчитываются как цепные и как базисные:
| Показатель | Базисный | Цепной |
| Абсолютный прирост (Diбаз и Diцеп ) | Уi –У0 илиУi –У1 | Уi –Уi-1 |
| Коэффициент роста (Кр баз и Кр цеп) | Уi / У0 или Уi /У1 | Уi /Уi-1 |
| Темп роста (Т р) | К р *100 | К р *100 |
| Темп прироста (Тпр) | Тр-100 | Тр-100 |
Аналитические показатели ряда динамики надо представить в таблице:
Таблица 8. Анализ динамики.
| Год | Среднемесячная номинальная заработная плата работников образования, руб. | Абсолютный прирост, руб. | Коэффициент роста | Темп роста, % | Темп прироста,% | ||||
| цепной | базисный | цепной | базисный | цепной | базисный | цепной | базисный | ||
| 5429,7 | |||||||||
| 6983,3 | 1553,6 | 1553,6 | 1,286 | 1,286 | 128,6 | 128,6 | 28,6 | 28,6 | |
| 8778,3 | 3348,6 | 1,257 | 1,617 | 125,7 | 161,7 | 25,7 | 61,7 | ||
| 11316,8 | 2538,5 | 5887,1 | 1,289 | 2,084 | 128,9 | 208,4 | 28,9 | 108,4 | |
| 13293,6 | 1976,8 | 7863,9 | 1,175 | 2,448 | 117,5 | 244,8 | 17,5 | 144,8 | |
| 14075,2 | 781,6 | 8645,5 | 1,059 | 2,592 | 105,9 | 259,2 | 5,9 | 159,2 | |
| Итого | 59876,9 |
Среднее значение среднемесячной заработной платы за 6 лет определяется
Среднее значение среднемесячной заработной платы за 6 лет составляет 9979,48 руб.
Среднегодовой абсолютный прирост определяется
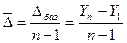
где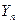 
- последний уровень ряда;
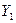- первый уровень ряда;
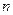- число уровней ряда.
Средний абсолютный прирост среднемесячной заработной платы равен 1729,10 руб.
Определим среднегодовые темпы роста и прироста.
Средний коэффициент роста определяется
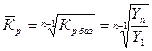
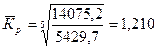
Среднегодовой темп роста определяется по формуле
Темп прироста равен Тпр = Тр -100 = 121 -100 = 21%
Абсолютное значение одного прироста определяется
| Показатель | Базисный | Цепной |
| Абсолютное значение одного процента прироста | У0(1) /100 | Уi-1/100 |
Рассчитаем его в таблице
| Год | Среднемесячная номинальная заработная плата работников образования, руб. | Абсолютное содержание 1% прироста | ||
| цепной | базисный | |||
| 5429,7 | ||||
| 6983,3 | 54,3 | 54,3 | ||
| 8778,3 | 69,8 | 54,3 | ||
| 11316,8 | 87,8 | 54,3 | ||
| 13293,6 | 113,2 | 54,3 | ||
| 14075,2 | 132,9 | 54,3 | ||
| Итого | 59876,9 |
Из проведенных расчетов видно, что среднемесячная номинальная заработная плата за 6 лет увеличилась на 8645,50 руб. Темп роста ее составил 259,2%. Среднее значение составляет 9979,48 руб.. В среднем за год среднемесячная номинальная заработная плата увеличивалась на 1729,10 руб. или 21%. Среднегодовой темп роста и прироста за 6 лет составили соответственно 121% и 21%.
Проанализируем основную тенденцию развития методом аналитического выравнивания.
Таблица 10. Расчет показателей уравнения для построения линии тренда.
| Год | Среднемесячная номинальная заработная плата работников образования, руб. | t | t2 | yt | yt |
| 5429,7 | -3 | -16289,1 | 5576,38 | ||
| 6983,3 | -2 | -13966,6 | 7044,08 | ||
| 8778,3 | -1 | -8778,3 | 8511,78 | ||
| 11316,8 | 11316,8 | 11447,2 | |||
| 13293,6 | 26587,2 | 12914,9 | |||
| 14075,2 | 42225,6 | 14382,6 | |||
| Итого | 59876,9 | 41095,6 | 59876,88 |
Уравнение тренда имеет вид yt=a0+a1t
Решим систему уравнений
a0*n = Σy
a1*Σt2 = Σty
a0*6 = 59876,9
a1*28 = 41095,6
Решая уравнения, получаем
а0 = 9979,48 руб.
а1 = 1467,7 руб.
Уравнение прямой примет вид
yt= 9979,48+1467,7*t
По уравнению получаем новый ряд данных (проставим в таблице).
Изобразим ряды динамики графически.
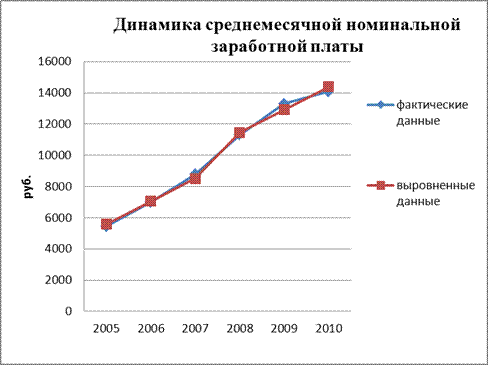
Рис. 2 Сглаживание методом аналитического выравнивания.
Прогноз среднемесячной номинальной заработной платы на 2011 и 2012 годы
yt2011=9979,48+1467,7*4 = 15850,28 руб.
yt2012=9979,48+1467,7*5 = 17317,98 руб.
Видим, что среднемесячная номинальная заработная плата имеет тенденцию к росту.
4.2
Проведем анализ внутригодовой динамики инвестиций в основной капитал (рассчитаем индексы сезонности). Изобразим сезонную волну графически.
Таблица 11. Расчет индексов сезонности.
| Месяцы | Инвестиции в основной капитал, млрд.руб. | Индекс сезонности
| ||
В среднем за 3 года 
| ||||
| Январь | 331,7 | 16355,8 | 5562,5 | 282,3 |
| Февраль | 421,5 | 17461,3 | 5960,9 | 302,5 |
| Март | 489,7 | 18535,9 | 6341,9 | 321,9 |
| Апрель | 527,2 | 590,1 | 372,4 | 18,9 |
| Май | 642,2 | 752,9 | 465,0 | 23,6 |
| Июнь | 793,1 | 565,0 | 28,7 | |
| Июль | 683,9 | 495,3 | 25,1 | |
| Август | 794,7 | 925,2 | 573,3 | 29,1 |
| Сентябрь | 882,9 | 1045,9 | 642,9 | 32,6 |
| Октябрь | 931,2 | 1149,4 | 693,5 | 35,2 |
| Ноябрь | 977,7 | 1192,3 | 723,3 | 36,7 |
| Декабрь | 1676,3 | 1246,8 | 63,3 | |
Средний уровень ряда 
| 762,7 | 5148,1 | 1970,2 | 100,0 |
По рассчитанным индексам сезонности изобразим сезонную волну на графике.
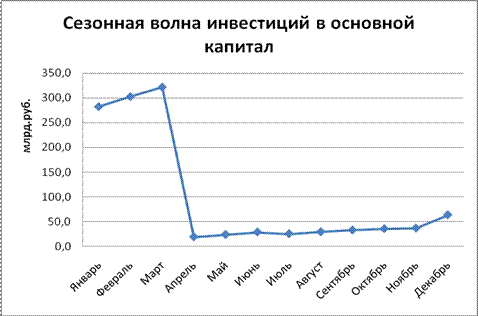
Рис. 3 Сезонная волна инвестиций в основной капитал
Видим, что в апреле инвестиции в основной капитал резко падали.
