Статистической гипотезой называется предположение о свойстве генеральной совокупности, которое можно проверить, опираясь на данные выборки. Гипотеза о распределениях параметров генеральной совокупности называется параметрической. Гипотеза о законах распределения называется непараметрической. Гипотеза о том, что две совокупности, сравнимые по одному или нескольким параметрам, ничем не отличаются, называется нулевой.
Правила, устанавливающие условия отклонения или принятия нулевой гипотезы, называются статистическим критерием.
Этапы проверки статистических гипотез:
- формулировка гипотезы;
- выборы статистического критерия;
- определение области допустимых значений и критических точек, которые разделяют область допустимых значений и определение критической области по соответствующим таблицам;
- вычисление фактического значения статистического критерия;
- проверка гипотезы на основе сравнения фактического и критического значения.
Возможны два ошибочных решения:
1) неправильное отклонение нулевой гипотезы (ошибка первого рода), ее вероятность или риск 
называется уровнем значимости критерия;
2) неправильное принятие нулевой гипотезы или ошибки второго рода, ее вероятность или риск 
, 
называется мощностью критерия.
Проверка соответствия теоретического и эмпирического распределения производится с помощью критериев согласия, наиболее распространенные из которых это - критерий Пирсона и Колмогорова. По ряду распределения строится гистограмма, вычисляются различные величины и на их основе подбирается тот или иной закон.
Критерий Пирсона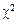 
проверяет гипотезу о том, что случайная выборка извлечена из генеральной совокупности с функцией распределения 
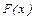, вид которой известен, а параметры неизвестны.
Этапы проверки гипотезы по критерию Пирсона
1. Совокупность преобразуется в интервальный ряд, который имеет k интервалов.
2. На основе сгруппированных данных вычисляются оценки неизвестных параметров теоретического распределения.
3. Определяют вероятность 
попадания случайной величины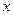 
в k -й интервал.
4. Вычисляется значение критерия Пирсона 
- чем меньше критерий, тем ближе фактическое распределение к теоретическому.
Критерий Пирсона сравнивается с табличным значением, найденным для уровня значимости 
и числа степеней свободы 
, где 
- число параметров закона распределения. Если полученное значение критерия больше критического, то нулевая гипотеза отвергается.
Критерий Колмогорова 
проверяет гипотезу о том, что случайная выборка, извлеченная из генеральной совокупности с непрерывной функцией распределения 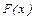, которая полностью определена, т.е. не зависит от неизвестных параметров.
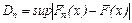, т.е. максимальный модуль отклонения эмпирической функции распределения от теоретической. Если данный критерий больше критического значения, то нулевая гипотеза отвергается.
Проверка гипотезы о средних
1. 
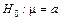, в качестве критерия используется критерий Стюарта 
, 
. Если значение 
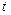- критерия больше критического, то нулевая гипотеза отвергается.
|
Проверка гипотезы о дисперсиях 
Проверка проводится с помощью критерия Фишера 
. Критическое значение данного критерия зависит от уровня значимости и числа степеней свободы числителя и знаменателя. Если значение критерия Фишера больше критического, то нулевая гипотеза отвергается.
Задачи
k – номер варианта
Задача 1
Каким должен быть объем случайной бесповторной выборки из генеральной совокупности численностью 10 000 единиц при сред-нем квадратическом отклонении не более 20+ k, предельной ошибке, не превышающей 5 %, и вероятности 0,997- k? (Нормальный закон распределения приведен в таблице приложения [4,5].)
Задача 2
С целью определения трудоемкости изготовления деталей на предприятии проведен хронометраж работы 50 рабочих, отобранных в случайном порядке. По данным обследований получили 
= 10+ k мин., 
= 1 мин. Определите:
а) как изменится ошибка выборки, если объем выборочной совокупности увеличить в 1,5 раза?
б) как скажется на ошибке выборки увеличение дисперсии в 2 раза?
в) как изменится ошибка выборки, если с увеличением дисперсии в 1,44 раза объем выборочной совокупности увеличить в 2,56 раза?
г) как изменится ошибка выборки, если численность генеральной совокупности будет в 3 раза больше?
