1. Однородность и вариация в массовых явлениях.
2. Средние величины.
3. Структурные характеристики вариационного ряда.
4. Показатели вариации.
Однородность и вариация в массовых явлениях
Массовые явления обладают как общими для всей совокупности, так и индивидуальными свойствами. Различия между индивидуальными явлениями называется вариацией. Взаимодействие элементов совокупности ведет к ограничению вариации, хотя бы части их свойств. Эта тенденция обусловливает применение средних величин в теории и на практике. Замена множества индивидуальных значений признака средней величиной, характеризующей всю совокупность, является обобщающая функция средней. При этом варианту можно представить следующим образом: 
Δ xi, где x i - варианта, с - общность, которая характеризуется средними величинами, Δ xi - индивидуальность, которая характеризуется показателями вариации.
Широкое применение средних объясняется тем, что они имеют ряд положительных свойств, делающих их незаменимыми в анализе явлений и процессов общественной жизни.
Средние величины
Средняя, являясь обобщенной характеристикой всей статистической совокупности, должна ориентироваться на определенную величину, связанную со всеми единицами этой совокупности.
Эту величину можно представить в виде функции F(x1,x2,x3,...,xn).
Так как данная величина в большинстве случаев отражает реальную экономическую категорию, ее называют определяющим показателем.
Если в F(x1,x2,x3,...,xn) все величины x1,x2,...,xn заменить их средней величиной *, то значение функции должно остаться прежним.
Раскрытие функции F(x1,x2,x3,...,xn) приводит к построению разных средних, наиболее широко используются степенные средние вида: 
.
Придавая z различные значения, получим различные виды средних.
При Z = -1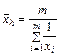 
- средняя гармоническая;
Z=0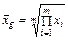 
- средняя геометрическая;
Z=1 
- средняя арифметическая;
Z=2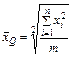 
- средняя квадратическая.
Все средние связаны правилом, которое называется правилом мажорантности средних:
Xh<=Xg <= Xa<=Xq.
Рассмотренные средние называются простыми и применяются при изучении вариации признака от объекта к объекту и связи признаков. Если средняя величина служит для характеристики обобщенных показателей системы, то используются не простые, а взвешенные средние.
Обобщающая формула для взвешенных средних следующая: 
, где f - веса вариант, частоты или частности.
; 
; 
; 
.
Наиболее часто в качестве средних используется средняя арифметическая (при вычислении которой общий объем признаков совокупности остается неизменным).
Свойства арифметической средней величины
1. Сумма отклонений индивидуальных значений признака от его среднего значения равна нулю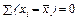 
.
2. Если каждое индивидуальное значение признака умножить или разделить на постоянное число, то и средняя увеличится или уменьшится во столько же раз 
, где а - постоянное число.
3. Если к каждому индивидуальному значению признака прибавить или из каждого значения вычесть постоянное число, то и средняя величина возрастет или уменьшится на столько же 
.
4. Если веса средней взвешенной умножить или разделить на постоянное число, средняя величина не изменится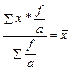 
.
Следствия:
- вместо абсолютных значений весов можно использовать доли или проценты;
- если все веса равны, то средняя арифметическая равна средней арифметической взвешенной.
5. Сумма квадратов отклонений индивидуальных значений признака от средней арифметической меньше, чем от любого другого числа 
.
Правила выбора средней
1. Средняя арифметическая используется, если известны численные значения знаменателя формулы, а значения числителя могут быть получены произведением.
2. Средняя гармоническая используется, если известны числовые значения числителя, а значения знаменателя могут быть получены как частные от деления показателя.
3. Средняя геометрическая применяется, если необходимо найти значение признака, качественно равноудаленного от максимального и минимального значения.
4. Средняя квадратическая применяется для измерения вариации признаков совокупности, что обусловлено 5-м свойством средней арифметической.
5. Средняя хронологическая используется, если данные представлены не за какой-либо период, а по состоянию на дату.
