Рассмотрим пример создания зашумленного сигнала, содержащего две синусоидальные компоненты. В начале создания некоторого сигнала необходимо задать вектор времени t:
>> t = (0:.01: 2.55);
Эта команда задает изменение t от 0 до 2.55 с шагом 0.01, что соответствует частоте дискретизации 100 Гц (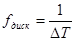
). Знак; (точка с запятой) блокирует вывод вектора на экран. Если необходимо просмотреть столбец с элементами вектора t, этот знак нужно просто убрать.
Теперь зададим вектор функции y(t), которая представляет собой сумму синусоиды с амплитудой 10 и частотой 7 Гц с синусоидой, имеющей амплитуду 3 и частоту 3 Гц:
>> y = 10*sin(2*pi*7*t) + 3*sin(2*pi*3*t);
Наложим на созданный сигнал аддитивный шум, моделируемый с помощью генератора случайных чисел, распределенных по нормальному закону. Для его инициации можно использовать команду:
>> randn(‘state’, sum(100*clock));
Получим шумовую компоненту со средним значением 1.5 и дисперсией 2, для этого используем команду:
>> yn = 1.5 + sqrt(2)*randn(size(t));
Наложим ее на «чистый» сигнал:
>> sig = y + yn;
Для просмотра полученных сигналов и оценивания спектра воспользуемся встроенной в систему Matlab утилитой sptool. Используем команду:
>> sptool
Откроется окно, состоящее из трех списков и управляющих кнопок. В настоящий момент нас интересует только первый и третий – Signals и Spectra. В первом отображаются загруженные в утилиту сигналы. По умолчанию в нем уже присутствуют три встроенных – mtlb, chirp и train.
Добавим в этот список два сгенерированных нами сигнала – y и sig. Для этого необходимо выбрать пункт Import в меню File. В появившемся окне необходимо выбрать нужный сигнал – y и нажать кнопку со стрелкой, дополнительно необходимо ввести частоту дискретизации – sampling frequency, в нашем случае – 100 Гц. Также в этом окне вводится имя нашего сигнала, по умолчанию используются имена sig1, sig2 и так далее. После нажатия кнопки “ОК” в первом списке утилиты появится новый сигнал – sig1. Просмотреть его можно, нажав кнопку View, находящуюся снизу списка Signals. Аналогично добавим сигнал sig. Возможен одновременный просмотр нескольких сигналов данных. Для этого удерживая нажатой клавишу ctrl, выбираем нужные с помощью мыши и нажимаем кнопку View. При просмотре сразу двух сигналов можно проследить изменения в зашумленных данных.
Для получения спектральной оценки необходимо выбрать нужный сигнал из списка Signals и нажать кнопку Create – откроется окно Spectrum Viewer. В нем задается тип спектральной оценки и ее параметры. В текущей работе мы рассмотрим периодограммный метод спектрального оценивания. В системе Matlab ему соответствует функция pwelch или метод Welch в окне Spectrum Viewer.
Параметры этой ценки:
– Nfft – число отсчетов в итоговой оценке спектра.
– Nwind – число отсчетов на сегмент данных – соответствует ранее введенному параметру D.
– Window – тип окна с помощью которого производится взвешивание отсчетов на каждом сегменте – w.
– Overlap – число перекрывающихся отсчетов между соседними сегментами – соответствует разности параметров D и S.
Расчет спектральной оценки осуществляется по нажатию кнопки Apply.
Аналогично выводу отсчетов сигналов данных возможен вывод нескольких спектральных оценок на одном графике. В меню Options утилиты можно выбрать тип масштаба по каждой из осей – линейный или логарифмический, а также диапазон выводимых частот [0, Fдиск/2],
[-Fдиск/2, Fдиск/2], [0, Fдиск].
Задание
1. Сформируйте два синусоидальных сигнала частотой 16 Гц с частотой дискретизации 250 Гц. Длина первого сигнала — 8 секунд (целое число периодов), второго — 7,65 секунды (нецелое число периодов). Импортируйте сигналы в утитилиту sptool и получите спектральные оценки этих сигналов с помощью преобразования Фурье (метод FFT).
Проанализируйте полученный результат.
2. Сформируйте двухкомпонентный сигнал длины 2,56 секунды со свойствами:
– частота дискретизации – 100 Гц;
– первая компонента: амплитуда – 1, частота – 40 Гц;
– вторая компонента: амплитуда – 2, частота – 55 Гц.
Получите спектральную оценку этого сигнала с помощью обычного преобразования Фурье (метод FFT).
Проанализируйте полученный результат.
3. Сформируйте четыре 256-точеченых окна: прямоугольное, треугольное, Ханна, Хемминга. Для этого используйте стандартные функции – rectwin(n), triang(n), hanning(n), hamming(n), где n – длина окна. Импортируйте полученные данные в утитилиту sptool и получите последовательно четыре спектральных оценки с помощью обычного преобразования Фурье (метод FFT). Совместите эти четыре оценки на одном графике и сравните их. Для удобства используйте различные цвета для каждой оценки.
Проанализируйте полученный результат и предложите ситуации, в которых более выгодно применять тот или иной тип окна.
Для одного из использовавшихся выше типов окон (по вашему выбору) сформируйте его 512-точечную реализацию. Получите аналогичную оценку спектра и сравните их.
4. Сформируйте три выборки двухкомпонентного сигнала длины 256, 512 и 1024 отсчета со следующими параметрами:
– частота дискретизации – 100 Гц;
– первая компонента: амплитуда – 10, частота – 15 Гц;
– вторая компонента: амплитуда – 2, частота – 35 Гц.
Получите спектральные оценки для каждого из сигналов, используя периодограмный метод (Welch), и совместите их на одном графике.
Добавьте к каждой реализации сигнала шумовую компоненту соответствующей длины со значением дисперсии 30. Получите оценку спектра.
Проанализируйте и объясните результаты оценки зашумленного сигнала. Сравните результаты при использовании различных окон (использовавшихся в п. 3 задания).
5. Сформируйте три реализации двухкомпонентного сигнала длины 256, 512 и 1024 отсчета с компонентами одинаковой мощности и разнесенными частотами на 0.2 Гц.
Получите спектральные оценки для каждого из сигналов, добившись разрешения частотных компонент, если это возможно. Объясните полученные результаты.
6. Проанализируйте вибрационные сигналы, полученные от исправного и неисправного вертолетов (Ispravn.txt, Neispravn.txt).
Для этого в меню File выберите пункт Import Data…. В окне Import выберите нужный файл и нажмите Open. В появившемся окне нажмите Next. В следующем окне нажмите Finish. В результате будет сформирован массив, имя которого будет совпадать с именем импортированного файла. Импортируйте полученные данные в утитилиту sptool и получите спектральные оценки с помощью преобразования Фурье (метод FFT). Частота дискретизации для каждого из сигналов равна 1953,125 Гц. Число отсчетов — 8192.
Обратите внимание на спектр данных сигналов при частотах 15 и 18 Гц.
Контрольные вопросы
1. Сформулируйте теорему отсчетов (Котельникова).
2. Напишите формулы прямого и обратного дискретного преобразования Фурье.
3. Что такое периодограмма?
4. Суть методов периодограммной оценки Даньелла, Бартлетта и Уэлча.
5. С какой целью применяются оконные (весовые) функции?
6. Каким образом можно избавиться от эффекта наложения (маскировки) при дискретизации реальных сигналов?
7. Как определяется разрешающая способность спектрального анализа на основе ДПФ?
