ЛАБОРАТОРНАЯ РАБОТА
СПЕКТРАЛЬНЫЙ АНАЛИЗ СЛОЖНЫХ СИГНАЛОВ
НА ОСНОВЕ МЕТОДА ПЕРИОДОГРАММ
Минск 2006
1. СПЕКТРАЛЬНЫЙ АНАЛИЗ СЛОЖНЫХ СИГНАЛОВ
НА ОСНОВЕ МЕТОДА ПЕРИОДОГРАММ
Цель работы: Изучить периодограммный метод спектрального анализа с помощью дискретного преобразования Фурье (ДПФ) на основе алгоритмов быстрого преобразования Фурье (БПФ).
Преобразование Фурье
Как известно, прямое и обратное преобразования Фурье для непрерывных сигналов определяются следующим образом:
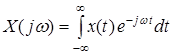
| (1) | |
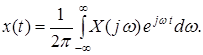
| (2) |
Для дискретных сигналов выражения (1) и (2) представляются в виде:
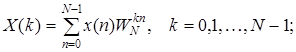
| (3) | |
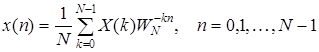
| (4) |
где
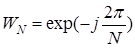 ;
;
x (n) ¾ выборочное значение входного сигнала;
X (k) ¾ коэффициент Фурье;
N ¾ объем выборки.
Выражения (3) и (4) похожи друг на друга, откуда следует, что эта пара преобразований может быть реализована с помощью одной и той же вычислительной процедуры. Однако прямое вычисление N -точечного ДПФ требует выполнения числа операций порядка N 2, быстро растущего с увеличением N и ведущего к огромной затрате вычислительных ресурсов при такой реализации вычислений. Поэтому настоятельной потребностью является разработка эффективных алгоритмов вычисления ДПФ, позволяющих значительно сократить число необходимых для этой цели арифметических операций и объем памяти. Появление таких алгоритмов, известных в настоящее время под общим названием алгоритмы быстрого преобразования Фурье (БПФ), обеспечило увеличение быстродействия при использовании метода Фурье в цифровой обработке сигналов, что заметно расширило сферу практического использования частотных представлений. БПФ позволяет вычислять ДПФ с числом операций, пропорциональным NlogN. При этом значительно уменьшилась вычислительная сложность и погрешности вычислений.
Классические методы спектрального оценивания
Классические методы спектрального оценивания обеспечивают получение гладких и статистически устойчивых спектральных оценок по конечному числу отсчетов данных. В результате применения данных методов получают оценки спектральной плотности мощности (СПМ). СПМ характеризует распределение энергии сигнала по частоте, отнесенной к единице времени. Различают два метода, относящихся к классическим — это периодограммный и коррелограммный. Оценки СПМ, основанные на прямом преобразовании данных и последующем усреднении, получили название периодограмм. Оценки СПМ, для получения которых по исходным данным сначала формируются корреляционные оценки и затем на их основе сама оценка, получили название коррелограммных методов спектрального оценивания.
До широкого распространения электронных вычислительных машин в основном применялся коррелограммный метод. Но с появлением алгоритмов БПФ и специализированных интегральных микросхем для обработки сигналов предпочтение стало отдаваться методам, основанным на использовании периодограмм.
Классические методы спектрального оценивания относятся к числу наиболее устойчивых методов спектрального оценивания. Они применимы почти ко всем классам сигналов и шумов, обладающих стационарными свойствами. В классических методах, как правило, используется алгоритм БПФ, в связи с чем они оказываются наиболее вычислительно эффективными методами из числа имеющихся методов спектрального оценивания.
Основной недостаток классических методов спектрального оценивания обусловлен искажающим воздействием просачивания по боковым лепесткам из-за неизбежного взвешивания в них конечных последовательностей данных. Обработка с помощью окна позволяет ослабить влияние боковых лепестков, но лишь за счет ухудшения спектрального разрешения.
Окна
Одним из важных вопросов, который является общим для всех классических методов спектрального оценивания, связан с применением функции окна. Обработка с помощью окна используется для управления эффектами, обусловленными наличием боковых лепестков в спектральных оценках.
Заметим, что имеющуюся конечную запись данных удобно рассматривать как некоторую часть соответствующей бесконечной последовательности, видимую через применяемое окно. Например, последовательность наблюдаемых данных x0(n) из N отсчетов математически можно записать как произведение прямоугольной функции единичной амплитуды ПN(n) и бесконечной последовательности x(n):
| x0(n)= x(n)∙ПN(n) 0£ n £ N- 1 | (6) |
Дискретное преобразование Фурье (ДПФ) взвешенной окном последовательности, выраженное через преобразование последовательности x(n) и прямоугольного окна ПN(n), равно свертке этих преобразований:
| X0(f) = X(f)*DN (f), | (7) |
где DN (f) – ядро Дирихле, представляющее собой ДПФ прямоугольной функции.
Взвешивание приводит к тому, что минимальная ширина спектральных пиков взвешенной окном последовательности ограничена шириной, определяемой главным лепестком преобразования этого окна, и не зависит от исходных данных. Боковые лепестки преобразования окна, иногда называемые просачиванием, будут изменять амплитуды соседних спектральных пиков.






