| Показники | Роки | ||||||||||
| Загальна кількість зареєстрованих злочинів | |||||||||||
| Коефіцієнт росту до 1996 р. | - | 0,95 | 0,93 | 0,91 | 0,9 | 0,82 | 0,73 | 0,9 | 0,84 | 0,79 | 0,68 |
| Коефіцієнт росту до попереднього року | - | 0,95 | 0,98 | 0,97 | 0,99 | 0,91 | 0,89 | 1,23 | 0,93 | 0,93 | 0,87 |
| Темп росту до 1996 р. (у %) | 95,5 | 93,3 | 90,5 | 89,7 | 81,6 | 90,1 | 84,3 | 78,7 | 68,2 | ||
| Темп росту до попереднього року (у %) | 95,5 | 97,8 | 99,1 | 89,5 | 123,5 | 93,5 | 93,4 | 86,7 | |||
| Темп приросту до 1996 р. (у %) | - | -4,5 | -6,7 | -9,5 | -10,3 | -18,4 | -27 | -9,9 | -15,7 | -21,3 | -31,8 |
| Темп приросту до попереднього року (у %) | - | -4,5 | -2,2 | -3 | -0,9 | -9 | -10,5 | 23,5 | -6,5 | -6,6 | -13,3 |
Добуток ланцюгових коефіцієнтів росту дорівнює базисному коефіцієнту росту за останній рік аналітичного періоду. Ділення базисного коефіцієнту росту на аналогічний показник попереднього року дає ланцюговий коефіцієнт росту за цей рік.В процесі аналізу динаміки злочинності доцільно використовувати як базисні, так і ланцюгові показники. Це дозволить більш повно і всебічно охарактеризувати процес динаміки в цілому та визначити його особливості в окремі роки періоду, який аналізується.
При підготовці аналітичного документу часто використовуються або тільки ланцюгові або тільки базисні показники динаміки. В будь–якому випадку треба чітко зазначати, який саме показник динаміки використовується в аналізі.
Для формулювання узагальненої оцінки ряду динаміки використовуються також середні показники. Середня являє собою величину, до якої найбільше наближені всі рівні ряду динаміки. Вона є кількісним параметром центральної тенденції ряду динаміки й усуває річні коливання його рівнів в окремі роки. Середній показник використовується, якщо ряд динаміки є достатньо тривалим. Чим ряд динаміки більше, тим більш стійка середня.
Середня добре виражає основну тенденцію, якщо ряд динаміки протягом всього періоду аналізу змінюється в одному напрямі (зростання або зниження) і не має значних коливань, тобто є достатньо однорідним. За наявності таких коливань використання середньої є некоректним.
Існує декілька видів середньої. Для інтервального ряду динаміки абсолютних показниківрозраховується середня арифметична проста:
,
де 
– середня, 
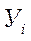– рівень ряду динаміки ί–го періоду, 
– кількість рівнів ряду динаміки, 
– знак суми.
Приклад
Середня кількість зареєстрованих злочинів протягом 1996-2006рр. складала: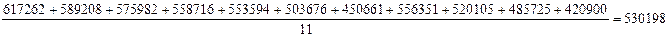 
Різниця між найбільшим (1996 р.) та найменшим (2006 р.) рівнями ряду динаміки складала 196362 тобто 32% від рівня базисного року, що дозволяє вважати середню арифметичну достатньо точною кількісною характеристикою стану зареєстрованої злочинності за цей період.
Якщо ряд динаміки охоплює тривалий період часу і ризниця між рівнями різних років є значною, можна застосовувати метод обрахування групових середніх, тобто розбивати ряд динаміки на декілька часових проміжків, які включають більш-менш однорідні величини рівнів ряду, та обчислювати середні за кожний з цих проміжків.
Приклад
На основі даних, наведеними у таблиці 8, можна обчислити наступні групові середні кількості зареєстрованих злочинів: 1972-1977 рр. – 140591, 1978-1988 рр. – 217949, 1989-1995 рр. – 475921, 1996-2006 рр. – 530198.
Аналогічним чином розраховується середній абсолютний приріст, але за умови збереження єдиної тенденції змін протягом всього аналізованого періоду.
Приклад
