Алгоритмы (свойства, реализация алгоритмов)

Алгоритм решения задачи – это система точных и понятных предписаний о содержании и последовательности выполнении конечного числа действий, необходимых для решения любой задачи данного типа.

Алгоритм – это конечный набор правил, последовательное применение которых к обрабатываемой информации за конечное число шагов позволяет получить результаты обработки (правила выполнения арифметических действий, правила решения определенных видов уравнений и т.д.).

Слово алгоритм появилось в результате искажения (после перевода на европейские языки) имени выдающего математика IX века Аль –Хорезми, которым были описаны правила выполнения основных арифметических действий в десятичной системе счисления. Понятие алгоритма возникло и используется ранее, чем появление ЭВМ.

Основные свойства алгоритма:

1. Дискретность, т.е. пошаговый характер определяемого им процесса. Описываемый процесс должен быть разбит на последовательность отдельных шагов. При каждом шаге работы алгоритма известно, что считать результатом шага.

2. Детерминированность (однозначность или определенность). Процесс применения правил к исходным данным определен вполне однозначно, результат работы алгоритма также будет однозначен. Запись алгоритма должна быть настолько четкой, полной, продуманной в деталях, чтобы у исполнителя не могло возникать потребности в принятии каких-либо самостоятельных решений, не предусмотренных составителем алгоритма.

3. Массовость. Необходимы алгоритмы, обеспечивающие решение широкого класса задач данного типа. Они предполагают возможность использовать различные допустимые значения исходящих данных.

Например: решение уравнения ах²+вх+с=0 в области действительных чисел может быть найдено по формуле:

_, которые применяемы не для одного, а для многих квадратных уравнений с коэффициентами а, в, с, удовлетворяющих условию

D=в² -4ас 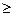0

4. Результативность. При точном исполнении всех предписаний алгоритма процесс должен прекратиться за конечное число шагов и при этом должен быть получен какой-либо определенный ответ на вопрос задачи.

Под алгоритмизацией понимают процесс разработки алгоритма решения какой-либо задачи.

Формы (способы) записи алгоритмов:

1) Словесный способ алгоритма – содержание последовательных шагов вычислений задается в произвольной форме на естественном языке. Например:

1. Прочитать заданное значение х.

2. Умножить х на 8.

3. Из результата второго действия (шага) извлечь квадратный корень.

4. К результату третьего действия прибавить 1.

5. Умножить х на 3.

6. Результат пятого действия разделить на результат четвертого действия.

7. Записать значение результата у.

Недостатки: низкая наглядность и слабая формализация. Этим способом можно описывать алгоритмы с произвольной степенью детализации.

2) Формульно-словесный способ основывается на задании последовательных шагов алгоритма с помощью математических формул и выражений в сочетании со словесными выражениями. Например:

1. Если Х>0, то перейти к шагу 2, в противном случае перейти к шагу 3.

2. Положить S= +D. Перейти к шагу 4.

3. Положить S=X-A. Перейти к шагу 4.

4. Принять S за искомый результат и остановиться.

Он более компактен и нагляден, но не является строго формальным.

3) Операторные схемы записи алгоритмов – это аналитическая форма представления алгоритма с помощью операторов, описывающих содержание отдельных участков вычислительного процесса. Участки алгоритма могут разделяться по своему назначению. Одни участки предусматривают вычисления с помощью арифметических операций, другие предназначены для проверки некоторых условий, выполнение которых определяет порядок работы алгоритма. Первые называются арифметическими операторами, вторые – логическими операторами. Имеется также группа специальных операторов управления (ввод-вывод данных, оператор останова и т.д.). Весь процесс решения задач состоит из последовательности выполнения таких операторов. Обозначения операторов:

B- ввод исходных данных

A- арифметический оператор

П - оператор печати (вывода)

Р - логический оператор

Я - оператор останова

Операторы имеют номера-индексы в соответствии с порядком их исследования. Логический оператор записывается как функция, аргументом которой служит проверяемое условие P (i=N) или P(υ ≤o)и т.д.

Операторы выполняются последовательно, которые могут нарушить логические операторы и безусловные операторы передачи управления. Если окажется, что проверяемое условие истинно, то очередным становится оператор, стоящий справа от логического оператора, в противном случае, когда логическое условие не соблюдается, оператор – приемник указывается стрелкой. Отсутствие передачи управления от оператора слева к соседнему оператору справа обозначается точкой с запятой (;). Алгоритм завершается оператором останова.

Операторная схема алгоритма сопровождается схемой счета.

Например:

Схема счета представлена в виде таблицы

 

№	Символ-оператор	Содержание оператора
	В1 Р2 А3 А4 П5 Я6	Ввод исходных данных Проверка выполнения логического условия (X>0) Вычисление значения Вычисление значения S= X-A Печать вычисленного значения S Останов
	Операторная схема выглядит следующим образом:   B1 P2 (х>0) А3; А4 П5 Я6

 

Ввел этот метод А.А. Ляпунов в 1954 году. Операторные схемы имеют формальный уровень, близкий к алгоритмическим языкам, и поэтому могут рассматриваться как средство автоматизации программирования.

4) Метод блок-схемы – это графическое изображение логической структуры алгоритма. На блок-схеме каждый этап процесса обработки представляется в виде геометрических фигур (блоков), имеющих определенную конфигурацию в зависимости от характера вычисляемых операций.

Блок может иметь имя (метку). Линия соединения блоков пока­зывает направление процесса обработки данных. Каждое направле­ние называется ветвью.

Перечень блоков, их наименование, функции, формы, разме­ры определяются ГОСТ 19.003—80. Указанный ГОСТ регламенти­рует изображение и размеры отдельных блоков в блок-схеме, а так­же их взаимное расположение. Основные виды блоков приведены в табл. 5.2.

Таблица 5.2

Блок-схемы алгоритмов

 

Наименование блока	Графическое представление блока	Функция блока
Линейный процесс		Выполнение операции или группы операций, в результате которых изменяются значение, форма представления или рас­положение данных
Проверка условия, логическое решение		Выбор направления выполне­ния алгоритма в зависимости от некоторых переменных ус­ловий
Ввод-вывод		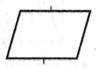Преобразование данных в фор­му, пригодную для обработки (ввод) или отображения резуль­татов обработки (вывод)
Начало-конец алгоритма (пуск-остановка)		Начало, конец процесса обра­ботки данных
Предопределенный (заранее описанный) процесс, модуль		Использование ранее создан­ных или отдельно описанных алгоритмов (модулей)
Соединитель		Указание связи между пре­рванными линиями потока об­работки данных

Например:

 

5) Псевдокод или структурно-стилизованный способ записи алгоритма основан на формализованном представлении предписаний. Разновидность: алгоритмический язык в русской нотации. Это например:

алг. запись

арг. истина

если ложь

нач. массив

кон.

Важнейшая особенность – близость к алгоязыкам программирования.

6) Язык программирования используется для записи алгоритмов в виде, непосредственно доступном ЭВМ.

Программа, написанная на языке программирования, представляет собой последовательность операторов, реализующих заданный алгоритм.

Языки программирования высокого уровня: ФОРТРАН, БЕЙСИК, КОБОЛ, АЛГОЛ, ПАСКАЛЬ, СИ, ПЛ/1 и др.

Например:

 

 

На языке Бейсик это выглядит следующим образом:

 

10 INPUT «Исх. данные», Х, D, А

20 IF X>0 THEN 5 Ø

30 S=Х- А

40 Goto 6 Ø

50 S=SQR (X) +D

60 PRINT «Результат=», S

70 END

Структуры данных

Структура данных относится, по существу, к "пространственным" понятиям: ее можно свести к схеме организации информации в памяти компьютера. Алгоритм же является соответствующим процедурным элементом в структуре программы - он служит рецептом расчета.

Первые алгоритмы были придуманы для решения численных задач типа умножения чисел, нахождения наибольшего общего делителя, вычисления тригонометрических функций и других. Сегодня в равной степени важны и нечисленные алгоритмы; они разработаны для таких задач, как, например, поиск в тексте заданного слова, планирование событий, сортировка данных в указанном порядке и т.п. Нечисленные алгоритмы оперируют с данными, которые не обязательно являются числами; более того, не нужны никакие глубокие математические понятия, чтобы их конструировать или понимать. Из этого, однако, вовсе не следует, что в изучении таких алгоритмов в математике нет места; напротив, точные, математические методы необходимы при поиске наилучших решений нечисленных задач при доказательстве правильности этих решений.

Структуры данных, применяемые в алгоритмах, могут быть чрезвычайно сложными. В результате выбор правильного представления данных часто служит ключом к удачному программированию и может в большей степени сказываться на производительности программы, чем детали используемого алгоритма. Вряд ли когда-нибудь появится общая теория выбора структур данных. Самое лучшее, что можно сделать,- это разобраться во всех базовых "кирпичиках" и в собранных из них структурах. Способность приложить эти знания к конструированию больших систем - это прежде всего дело инженерного мастерства и практики.

Независимо от содержания и сложности любые данные в памяти ЭВМ представляются последовательностью двоичных разрядов, или битов, а их значениями являются соответствующие двоичные числа. Данные, рассматриваемые в виде последовательности битов, имеют очень простую организацию или, другими словами, слабо структурированы. Для человека описывать и исследовать сколько-нибудь сложные данные в терминах последовательностей битов весьма неудобно. Более крупные и содержательные, нежели бит, "строительные блоки" для организации произвольных данных получаются на основе понятия "структуры данного".

Под структурой данных в общем случае понимают множество элементов данных и множество связей между ними. Такое определение охватывает все возможные подходы к структуризации данных, но в каждой конкретной задаче используются те или иные его аспекты. Поэтому вводится дополнительная классификация структур данных, направления которой соответствуют различным аспектам их рассмотрения. Прежде чем приступать к изучению конкретных структур данных, дадим их общую классификацию по нескольким признакам.

Понятие " физическая структура данных " отражает способ физического представления данных в памяти машины и называется еще структурой хранения, внутренней структурой или структурой памяти.

Рассмотрение структуры данных без учета ее представления в машинной памяти называется абстрактной или логической структурой. В общем случае между логической и соответствующей ей физической структурами существует различие, степень которого зависит от самой структуры и особенностей той среды, в которой она должна быть отражена. Вследствие этого различия существуют процедуры, осуществляющие отображение логической структуры в физическую и, наоборот, физической структуры в логическую. Эти процедуры обеспечивают, кроме того, доступ к физическим структурам и выполнение над ними различных операций, причем каждая операция рассматривается применительно к логической или физической структуре данных.

Различаются простые (базовые, примитивные) структуры (типы) данных и интегрированные (структурированные, композитные, сложные). Простыми называются такие структуры данных, которые не могут быть расчленены на составные части большие, чем биты. С точки зрения физической структуры важным является то обстоятельство, что в данной машинной архитектуре, в данной системе программирования мы всегда можем заранее сказать, каков будет размер данного простого типа и какова структура его размещения в памяти. С логической точки зрения простые данные являются неделимыми единицами. Интегрированными называются такие структуры данных, составными частями которых являются другие структуры данных - простые или в свою очередь интегрированные. Интегрированные структуры данных конструируются программистом с использованием средств интеграции данных, предоставляемых языками программирования.

В зависимости от отсутствия или наличия явно заданных связей между элементами данных следует различать несвязные структуры (векторы, массивы, строки, стеки, очереди) и связные структуры (связные списки).

Весьма важный признак структуры данных - ее изменчивость - изменение числа элементов и (или) связей между элементами структуры. В определении изменчивости структуры не отражен факт изменения значений элементов данных, поскольку в этом случае все структуры данных имели бы свойство изменчивости. По признаку изменчивости различают структуры статические, полустатические, динамические. Классификация структур данных по признаку изменчивости приведена на рис. 5.2. Базовые структуры данных, статические, полустатические и динамические характерны для оперативной памяти и часто называются оперативными структурами. Файловые структуры соответствуют структурам данных для внешней памяти.

Рис. 5.2. Классификация структур данных

Важный признак структуры данных - характер упорядоченности ее элементов. По этому признаку структуры можно делить на линейные и нелинейные структуры.

В зависимости от характера взаимного расположения элементов в памяти линейные структуры можно разделить на структуры с последовательным распределением элементов в памяти (векторы, строки, массивы, стеки, очереди) и структуры с произвольным связным распределением элементов в памяти (односвязные, двусвязные списки). Пример нелинейных структур - многосвязные списки, деревья, графы.

В языках программирования понятие "структуры данных" тесно связано с понятием " типы данных ". Любые данные, т.е. константы, переменные, значения функций или выражения, характеризуются своими типами.

Информация по каждому типу однозначно определяет:

1) структуру хранения данных указанного типа, т.е. выделение памяти и представление данных в ней, с одной стороны, и интерпретирование двоичного представления, с другой;

2) множество допустимых значений, которые может иметь тот или иной объект описываемого типа;

3) множество допустимых операций, которые применимы к объекту описываемого типа.

В вычислительной технике структура данных — это программная единица, позволяющая хранить и обрабатывать множество однотипных и/или логически связанных данных. Для добавления, поиска, изменения и удаления данных структура данных предоставляет некоторый набор функций, составляющих интерфейс структуры данных. Структуры данных формируются с помощью типов данных, ссылок и операций над ними в выбранном языке программирования.

Тип - относительно устойчивая, независимая совокупность элементов, которую можно выделить во всем рассматриваемом множестве (предметной области} Типы данных бывают следующие:

Простые.

Перечислимый тип может хранить только те значения, которые прямо указаны в его описании:

-числовые. Хранятся числа, могут применяться обычные арифметические операции;

-целочисленные: со знаком, то есть могут принимать как положительные, так и отрицательные значения, и без знака, то есть могут принимать только неотрицательные значения;

-вещественные: с запятой и с плавающей запятой;

-числа произвольной точности, обращение с которыми происходит посредством длинной арифметики;

-символьный тип. Хранит один символ, могут использоваться различные кодировки;

-логический тип: имеет два значения: истина и ложь, могут применяться логические операции. Используется в операторах ветвления и циклах. В некоторых языках является подтипом числового типа, при этом ложь=0, истина=1;

-множество. В основном совпадает с обычным математическим понятием множества. Допустимы стандартные операции с множествами и проверка на принадлежность элемента множеству. В некоторых языках рассматривается как составной тип.

Составные (сложные).

- массив — упорядоченный набор данных, для хранения данных одного типа, идентифицируемых с помощью одного или нескольких индексов. В простейшем случае массив имеет постоянную длину и хранит единицы данных одного и того же типа. Количество используемых индексов массива может быть различным. Массивы с одним индексом называют одномерными, с двумя — двумерными и т. д. Одномерный массив нестрого соответствует вектору в математике., двумерный — матрице. Чаще всего применяются массивы с одним или двумя индексами, реже — с тремя, ещё большее количество индексов встречается крайне редко;

- строковый тип. Хранит строку символов. Аналогом сложения в строковой алгебре является конкатенация (прибавление одной строки в конец другой строки). В языках, близких к бинарному представлению данных, чаще рассматривается как массив символов, в языках более высокой абстракции зачастую выделяется в качестве простого;

- запись (структура). Набор различных элементов (полей записи), хранимый как единое целое. Возможен доступ к отдельным полям записи. Например, struct в С или record в Pascal;

- файловый тип. Хранит только однотипные значения, доступ к которым осуществляется только последовательно (файл с произвольным доступом, включенный в некоторые системы программирования, фактически является неявным массивом).