При виводу ланцюжка ω в G на кожному кроку безпосереднього виведення коли ми беремо до уваги виділений нами нетермінал (в залежності від стратегії виведення), виникає питання, яку альтернативу для 
використати. З точки зору практики, нас цікавить така стратегія виведення 
в граматиці 
, коли кожний наступний крок безпосереднього виведення наближав би нас до мети. Ця стратегія дасть можливість виконати виведення в за час пропорційний 
, де 
. Зрозуміло, що не маючи інформації про структуру , досягнути вибраної нами мети в більшості випадків неможливо. Але ж тримати інформацію про весь ланцюжок також недопустимо. З точки зору практики, отримати потрібний результат розумно при наявності локальної інформації, наприклад, 
поточних вхідних лексем програми ( — наперед фіксоване число) достатньо для організації виведення в за час пропорційний . З точки зору синтаксичного аналізу ланцюжка мова ведеться про наступну ситуацію:
S
 |  |
ω1 A ω2
 |  |
ω1 X Y
Мал. 5
Зафіксуємо стратегію виводу: далі будемо розглядати лише лівосторонню стратегію виводу в . Тоді:
- 
(
— перший зліва направо нетермінал);
- 
- термінальна частина ланцюжка , яку вже виведено (проаналізована частина ланцюжка);
- результат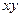 
, який потрібно ще вивести, виводиться з ланцюжка 
;
- щоб зробити вірний крок виведення (без повернення назад) нам було б достатньо поточних вхідних символів з непроаналізованої частини програми .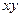
Сформульовані нами умови забезпечує клас 
-граматик.
Означення. КС-граматика 
називається 
-граматикою для деякого фіксованого , якщо дія двох лівосторонніх виводів виду:
1) 
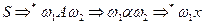
2) 
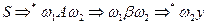, для яких з 
випливає, що 
, де 
.
Неформально, граматика буде -граматикою, якщо для ланцюжка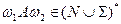 
перших символів (за умови, що вони існують) решти непроаналізованого ланцюжка визначають, що з існує не більше однієї альтернативи виведення ланцюжка, що починається з та продовжується наступними термінальними символами.
Означення.
Сформулюємо основні твердження стосовно класу -граматик:
1) Не існує алгоритма, який перевіряє належність КС-граматики класу -граматик.
2) Існує алгоритм, який для конкретного перевіряє, чи є задана граматика -граматикою.
3) Якщо граматика є -граматикою, то вона є 
-граматикою, (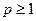
).
4) Клас -граматик — це підклас КС-граматик, який не покриває його.
Продемонструємо на прикладі справедливість твердження 4. Розглянемо граматику з наступною схемою 
:
Мова, яку породжує наведена вище граматика 
. Візьмемо виведення наступного ланцюжка 
; за означенням LL(K)-граматики 
, тоді 
маємо
Таким чином, КС-граматика не може бути -граматикою для жодного . Як результат, КС-граматика , яка має ліворекурсивний нетермінал (нетермінал називається ліворекурсивний, якщо в граматиці існує вивід виду 
), не може бути -граматикою.
З практичної точки зору в більшості випадків ми будемо користуватися 
-граматиками. У класі -граматик існує один цікавий підклас - це розподілені -граматики.
Означення. -граматика називаються розподіленою, якщо вона задовольняю наступним умовам:
- у схемі граматики відсутні 
-правила (правила виду 
);
- для нетермінала праві частини -правила починаються різними терміналами.
Для подальшого аналізу означення 
-граматики розглянемо алгоритм обчислення функції 
.
Означення: Якщо 
, то 
, де 
— бінарна операція над словарними множинами (мовами):
.
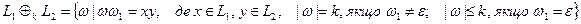Висновок, якщо 
, де 
, тоді
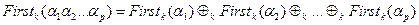
Очевидно, якщо 
, то 
при 
. Розглянемо алгоритм пошуку 
Алгоритм. Пошук множини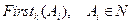 
.
Визначимо значення функції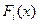 
для кожного 
.
П1. 
для всіх 
.
П2. 
в інших випадках - невизначено.
Пn.
в інших випадках - невизначено.
Пm. 
для всіх 
.
Очевидно, що:
- послідовність 
— монотонно зростаюча;
- 
— послідовність, обмежена зверху.
Тоді покладемо 
для кожного .
Приклад: Знайти множину Firstk(Ai) для нетерміналів граматики з наступною схемою правил:
S -> BA
A -> +BA | ε
B -> DC
C -> *DC | ε
D -> (S) | a
Нехай k=2.
| Fn\Ai | S | A | B | C | D |
| F0 | -- | { ε } | -- | { ε } | {a} |
| F1 | -- | { ε } | {a} | { ε, *a} | {a} |
| F2 | {a} | {ε, +a} | {a, a*} | { ε, *a} | {a} |
| F3 | {a, a+, a*} | {ε, +a} | {a, a*} | { ε, *a} | {a, (a} |
| F4 | {a, a+, a*} | {ε, +a} | {a, a*, (a} | { ε, *a, *(} | {a, (a} |
| F5 | {a, a+, a*, (a} | {ε, +a, +(} | {a, a*, (a} | { ε, *a, *(} | {a, (a} |
| F6 | {a, a+, a*, (a} | {ε, +a, +(} | {a, a*, (a} | { ε, *a, *(} | {a, (a, ((} |
| F7 | {a, a+, a*, (a} | {ε, +a, +(} | {a, a*, (a, ((} | { ε, *a, *(} | {a, (a, ((} |
| F8 | {a, a+, a*, (a, ((} | {ε, +a, +(} | {a, a*,(a, ((} | { ε, *a, *(} | {a, (a, ((} |
| F9 | {a, a+, a*, (a, ((} | {ε, +a, +(} | {a, a*, (a, ((} | { ε, *a, *(} | {a, (a, ((} |
Скористаємося означенням 
сформулюємо необхідні й достатні умови, за яких КС-граматика буде -граматикою:
для довільного виводу в граматиці G виду 
та правила 
:
(1)
Вище сформульована умова для -граматик може бути перефразована з урахуванням визначення множини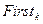 
:
для довільного виводу в граматиці виду та правила :
, де 
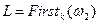(2).
Оскільки 
, то умова (2) є конструктивною умовою і може бути використана для перевірки, чи КС-граматика є -граматикою для фіксованого .
Означення: КС-граматика називається сильною -граматикою, якщо для А -правила виду задовольняється умова:
,
де 
визначається так:
Операції 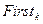та 
можна узагальнити для словарної множини 
, тоді:
.
Без доведення зафіксуємо наступні твердження:
- кожна -граматика є сильною -граматикою;
- існують -граматики (k>1), які не є сильними -граматиками.
На прикладі продемонструємо останнє твердження. Нехай граматика визначена наступними правилами:
, 
.
Відповідні множини 
, 
, 
,
.
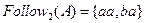Перевіримо умову для сильної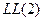 
-граматики:
а) виконаємо перевірку 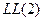-умови для правила
б) виконаємо перевірку 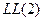-умови для правила
Висновок: вище наведена граматика не є сильною 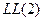-граматикою. Перевіримо цю ж граматику на властивість 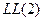-граматики. Тут ми маємо два різні варіанти виводу з S:
а) 
б) 
Висновок: наведена вище граматика є 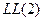-граматикою.
Алгоритм. Обчислення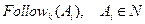 
.
Для побудови алгоритму пошуку множини 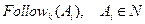розглянемо наступні приклади на синтаксичному дереві, які дозволять перейти до узагальнень.Подивимося на синтаксичне дерево висоти 1 для правила 
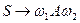S
ω1 A ω2
Мал. 6
Тоді 
.
Далі розглянемо дерево висоти 2:
S
 |
ω1 AJ ω2
 |  |
ω3 A ω4
Мал. 7.
Тоді 
. В силу вищесказаного, будемо знаходити значення функції 
, тобто будемо розглядати всілякі дерева, які можна побудувати, починаючи з аксіоми 
.
П0. 
. Очевидно, за 0 кроків ми виведемо S, після якої знаходиться . У інших випадках 
— невизначено 
.
П1. 
. В інших випадках 
— невизначено.
….
Пn 
. В інших випадках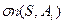 
— невизначено.
….
Настане крок Пm, коли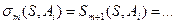 
, 
.
Тоді покладемо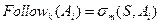 
для кожного .
Очевидно, що:
- послідовність 
монотонно зростаюча;
- 
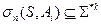послідовність обмежена зверху.
До того, як перевірити граматику на -властивість необхідно перевірити її на наявність ліворекурсивних нетерміналів та спробувати уникнути лівої рекурсії.
Означення: Нетермінал КС-граматики називається -нетерміналом, якщо 
.
Алгоритм. Пошук -нетерміналів:
….
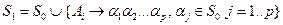
…. Пn
Тоді множина 
— множина -нетерміналів.
Приклад. Для граматики G з схемою правил Р знайдемо множину -нетерміналів:
= 
Таким чином, множина -нетерміналів для наведеної вище граматики - 
Алгоритм. Тестування нетермінала на ліву рекурсію. Для кожного нетермінала Аi побудуємо наступну послідовність множин S0, S1, ….
, починаємо з нетерміналу Аi.
….
….
Тоді якщо 
, то — ліворекурсивний нетермінал.
Приклад. Для граматики G з схемою правил Р знайдемо множину ліворекурсивних нетерміналів:
1. Виконаємо процедуру тестування для кожного нетермінала окремо:
- наприклад, для нетермінала S:
Запропонуємо декілька прийомів, що дають можливість при побудові 
граматик уникнути лівої рекурсії. Розглянемо граматику зі схемою правил , яка має ліворекурсивний нетермінал . Замінимо схему правил новою схемою з трьома правилами
.
Приклад: Для граматики G з схемою правил Р для кожного нетермінала знайдемо множину 
(k =1):
S -> BA
A -> +BA | ε
B -> DC
C -> *DC | ε
D -> (S) | a
З прикладу, що наведено раніше множини First1(A),будуть такими:
First1(S)= First1(B)= First1(D)={(,a}, First1(A)={+, ε }, First1(C)={*, ε }.
| δn\Ai | S | A | B | C | D |
| δ0 | { ε } | -- | -- | -- | -- |
| δ 1 | { ε } | { ε } | {+, ε } | -- | -- |
| δ 2 | { ε } | {ε} | {+, ε } | {+, ε } | |
| δ 3 | { ε } | {ε} | {+, ε } | {+, ε } | {*, +, ε } |
| δ 4 | { ε,) } | {ε} | {+, ε } | {+, ε } | {*, +, ε } |
| δ 5 | { ε,) } | {ε,)} | {+, ε } | {+, ε,)} | {*, +, ε } |
| δ 6 | { ε,) } | {ε,)} | {+, ε,)} | {+, ε } | {*, +, ε,)} |
| δ 7 | { ε,) } | {ε,)} | {+, ε,)} | {+, ε,)} | {*, +, ε,)} |
Таким чином, Follow1(S) = { ε,) }, Follow1(A) = {ε,)}, Follow1(B) = {+, ε,)}, Follow1(C) = {+, ε,)}, Follow1(D) = {*, +, ε,)}.
