| Сұрақ нөмірі | Тақырып номері | Күрделілік деңгейі | Дұрыс жауап |
| ACD | |||
| CE | |||
| BE | |||
| ACF | |||
| ACE | |||
| ADH | |||
| BDF | |||
| ACE | |||
| AEG | |||
| AF | |||
| ACF | |||
| AC | |||
| BDH | |||
| AC | |||
| BDC | |||
| B | |||
| ACG | |||
| BEF | |||
| AD | |||
| AFH | |||
| D | |||
| BF | |||
| D | |||
| BF | |||
| BDF | |||
| ADG | |||
| BD | |||
| CEH | |||
| AC | |||
| CEH | |||
| ADF | |||
| AC | |||
| CGH | |||
| BEH | |||
| BD | |||
| ADG | |||
| CDG | |||
| ADF | |||
| AE | |||
| DF | |||
| AC | |||
| A | |||
| A | |||
| ADF | |||
| AD | |||
| ADG | |||
| BE | |||
| DF | |||
| A | |||
| B | |||
| B | |||
| D | |||
| CEF | |||
| DEH | |||
| C | |||
| C | |||
| ABE | |||
| CEG | |||
| B | |||
| BDE | |||
| ADF | |||
| CG | |||
| BE | |||
| AEH | |||
| DEH | |||
| BEG | |||
| B | |||
| ADH | |||
| CEG | |||
| CDF | |||
| BEF | |||
| CFH | |||
| BEH | |||
| BDG | |||
| CGH | |||
| AFH | |||
| A | |||
| AEH | |||
| C | |||
| A | |||
| ADG | |||
| DGH | |||
| B | |||
| AEH | |||
| A | |||
| D | |||
| C | |||
| A | |||
| DF | |||
| FGH | |||
| AF | |||
| E | |||
| AE | |||
| C | |||
| BFH | |||
| AFG | |||
| DEH | |||
| BH | |||
| A | |||
| A | |||
Құрастырушы:
Т.ғ.к., доцент __________ А.Ш.Кажикенова
Математиканы және информатиканы оқыту әдістемесі
кафедрасының меңгерушісі __________ Н.К.Сыздыкова
Тестік тапсырмалар саны: 100
Құрастырылған күні: 31.03.13
ВОУД сынау-тестілеуіне арналған
$$$ 1
y= 
- функциясы үшін вертикаль асимптотаның теңдеуін жаз:
A) & x=1.
B) x=0.
C) & x-1=0.
D) & 1-x=0.
E) x=2.
F) y=-1-x.
G) y=x2.
H) y=x-1.
$$$ 2
f(x) функциясы өзінің анықталу облысындағы кез-келген х үшін жұп деп аталады, егер:
A) f(-x)=-f(x).
B) f(x2)=f(x).
C) & f(-x)=f(x).
D) f(2x)=f(x).
E) & f(x)=f(-x).
F) f(-2x)=f(x).
G) f(x)=-f(x).
H) y=x-1.
$$$ 3
f(x) функциясы өзінің анықталу облысындағы кез-келген х үшін тақ деп аталады, егер:
A) f(-x)=f(x).
B) & f(-x)=-f(x).
C) f(-x3)=-f(x).
D) f(-3x)=-f(x).
E) & - f(x)=f(-x).
F) f(2x)=f(x).
G) f(2x)=-f(2x).
H) f(x)=-f(x).
$$$ 4
Шекті есепте 
:
A) & e2.
B) e.
C) & 
.
D) e1/2.
E) 1.
F) & 
.
G) 2.
H) f(x)=-f(x).
$$$ 5
Шекті есепте 
:
A) & 
.
B) 3.
C) & 2-1.
D) 
.
E) & 0,5.
F) 5/7.
G) 1.
H) 
.
$$$ 6
Шекті есепте 
:
A) & 
.
B) 0.
C) 1.
D) & 
.
E) 5.
F) -3.
G) 3.
H) & 
.
$$$ 7
Шекті есепте 
:
A) a.
B) & 2a.
C) 0.
D) & 
.
E) -2a.
F) & 
.
G) 
.
H) 1.
$$$ 8
Шекті есепте 
:
A) & 
.
B) 6.
C) & -0,6.
D) 0,6.
E) & 
.
F) 
.
G) 1.
$$$ 9
Шекті есепте 
:
A) & 1.
B) 0.
C) 2.
D) ¥.
E) & lne.
F) –1.
G) & 20.
H) -¥.
$$$ 10
Бірінші тамаша шектің формуласы:
A) & 
.
B) 
.
C) 
.
D) 
.
E) 
.
F) & 
.
G) f(x)=-f(x).
$$$ 11
берілген. 
табу керек:
A) & 
.
B) 
.
C) & 
.
D) 
.
E)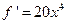 
.
F) & 
.
G) 
.
H) 
.
$$$ 12
Егер 
болса, y’ есепте:
A) & 2cos 2x.
B) cos 2x.
C) & –2(- cos2x).
D) –2cos2x.
E) -cos2x.
F) 2cos 2x.
G) -sin2x.
H) sin2x.
$$$ 13
функциясының туындысын есепте:
A) 
.
B) & 
.
C) 
.
D) &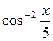 
.
E) 
.
F) 
.
G) 
.
H) & 
.
$$$ 14
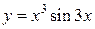функциясының туындысын есепте:
A) &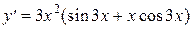 
.
B) 
.
C) & 
.
D)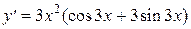 
.
E) 
.
F) 
.
G) 
.
H) 
.
$$$ 15
функциясының туындысын есепте:
A) 
.
B) & 
.
C) &.
D) &.
E) 
.
F) 
.
G) 
.
H) .
$$$ 16
Функция өсімшесінің Dу=f(x0+Dx)-f(x0) аргумент өсімшесі Dx-ке Dx-тің нөлге ұмтылғанда қатынасының шегі:
A) Бірінші тамаша шек.
B) & f(x) функциясының туындысы.
C) Екінші тамаша шек.
D) f(x) функциясының алғашқы бейнесі.
E) Функция.
F) Асимптота.
G) Шек.
H) Интеграл.
$$$ 17
Егер y(x)=ln(3x) болса,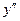 
табу керек:
A) & - 
.
B) - 
.
C) & 
.
D) 
.
E) 3lnx.
F) 3.
G) & 
.
H) 1.
$$$ 18
функциясының максимум нүктелерін анықтау керек:
A) -4.
B) & -2 lne.
C) 1.
D) 2; -2.
E) & 
.
F) & 
.
G) 2.
H) 0; 2.
$$$ 19
функциясының өсу аралығын тап:
A) & (-∞; -1) È (3; ∞).
B) (-∞; ∞).
C) (3; ∞).
D) & 
.
E) (-∞; -1) È (-1; 3) È (3; ∞).
F) (-1; 3).
G) (-1; 3) È (3; ∞).
H) .
$$$ 20
функциясы үшін кризистік нүктелерін тап:
A) & –2 және 0.
B) Кризистік нүктелері жоқ.
C) –2.
D) 
және 0.
E) 0 және 1.
F) & және 0.
G) –1 және 0.
H) & -2 lne және 0.
$$$ 21
y=f(x) функциясының x=x0 нүктесіндегі туындысы мынаған тең:
A) y=f(x) қисығына (x0,f(x0)) нүктесіне жүргізілген нормальдың көлбеулік бұрышының тангенсіне тең.
B) Қисықтың OX осімен жасайтын бұрышының тангенсіне тең.
C) Қисықтың OY осімен жасайтын бұрышының тангенсіне тең.
D) & y=f(x) функцмясына (x0,f(x0)) нүктесінде жүргізілген жанаманың көлбеулік бұрышының тангенсіне тең.
E) 0.
F) C+31ex.
G) -31ex + C.
H) ex+C.
$$$ 22
неге тең:
A) 31ex-1 + C.
B) & 31ex + C.
C) 31ex+1 + C.
D) exln31 + C.
E) 31.
F) & C+31ex.
G) -31ex + C.
H) ex+C.
$$$ 23
F(x) функциясы f(x) функциясы үшін алғашқы образ деп аталады, егер барлық х үшін... болса:
A) F¢(-x) = f(x).
B) F(x)dx = f(x).
C) F(x) = f(x)dx.
D) & F¢(x) = f(x).
E) F(x) = f(x).
F) C+31ex.
G) -31ex + C.
H) ex+C.
$$$ 24
Бөліктеп интегралдау формуласы:
A) 
.
B) & 
.
C) 
.
D) .
E) 
.
F) &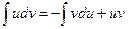 
.
G) 
.
H) ex+C.
$$$ 25
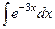интегралды еcепте:
A) 
.
B) & 
.
C) 
.
D) & 
.
E) 
.
F) & 
.
G) 
.
H) 
.
$$$ 26
интегралды еcепте:
A) & 
.
B) 
+ C.
C) (4x-1) 
+ C.
D) & 
.
E) 
.
F) 
+ C.
G) & 
.
H) 
.
$$$ 27
интегралды еcепте:
A) cos(a-bx) + C.
B) & 
.
C) - b cos(a-bx) + C.
D) & 
.
E) - .
F) b cos(a-bx) + C.
G) 
.
H)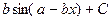 
.
$$$ 28
интегралды еcепте:
A) 
.
B) 
.
C) & - 
e 
+ C.
D) -2 e + C.
E) & 
.
F) -e + C.
G) 
.
H) & 
.
$$$ 29
интегралды еcепте:
A) & 
.
B) 
.
C) & - 
.
D) 
.
E) 
.
F) 
.
G) 
.
H) 
.
$$$ 30
интегралды е епте:
A) cos4 x + C.
B) sin4 x + C.
C) & 
.
D) sin3 x cos x + C.
E) & 
.
F) 
.
G) 
.
H) & 
.
$$$ 31
интегралды еcепте:
A) & arctg (x +2) + C.
B) tg (x +2)+ C.
C) arctg (x +4) + C.
D) & arctg (2 + x) + C.
E) arctg (4 x +5) + C.
F) & 20 arctg (x +2) + C.
G) arctg x + C.
H) ex+C.
$$$ 32
интегралды еcепте:
A) & 
.
B) 
arcctg 
+ C.
C) & 
.
D) 
+ C.
E) 
+ C.
F) 
.
G) 
.
H) ex+C
$$$ 33
интегралды еcепте:
A) (ln t)5 + C.
B) 5ln t + C.
C) &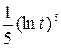 
+ C.
D) 
+ C.
E) - + C.
F) lnt+C.
G) & 0,2 
.
H) & 5-1 .
$$$ 34
интегралды еcепте:
A) 1.
B) & .
C) 
.
D) 
.
E) & 0,5.
F)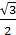 
.
G) 3.
H) & 2-1.
$$$ 35
интегралды еcепте:
A) 2.
B) & ln (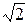
+1).
C) 4.
D) & ln (1 + ).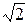
E) ln (1 + 
).
F) 1.
G) 3.
H) 2-1.
$$$ 36
интегралды еcепте:
A) & 3(e -1).
B) 9(e-1).
C) 
.
D) & 3e-3.
E) 3(1 - e).
F) 3-3e.
G) & -3+3e.
H) 9e+1.
$$$ 37
интегралды еcепте:
A) 5.
B) 2.
C) & 2 
.
D) & 
.
E) 
.
F) 3
G) &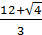 
.
H) 1.
$$$ 38
Интегралды еепте 
:
A) & 
.
B)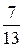 
.
C) 
.
D) &.
E) 
.
F) & 
.
G)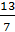 
.
H) 1.
$$$ 39
неге тең:
A) & F(b)-F(a), где 
(x) = f(x).
B) F(b)+F(a).
C)2 F(b).
D) 0.
E) & - F(a)+F(b), где (x) = f(x).
F) 
.
G) .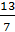
H) 1.
$$$ 40
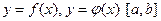интервалында 
сызықтарымен шектелген фигураның ауданы қай формуламен есептеледі:
A) .
B)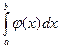 
.
C)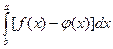 
.
D) & 
.
E) 
.
F) & 
.
G) .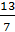
H) 1.
$$$ 41
ОХ осінен айналдырғанда шығатын айналу денесінің көлемі:
A) &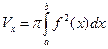 
.
B) 
.
C) & 
.
D) 
.
E) 
F) 
.
G) .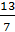
H) 1.
$$$ 42
нені белгілейді:
A) & Анықталған интеграл.
B) Нүкте.
C) Түзу.
D) Жазықтық.
E) 0.
F) Үдеу.
G) Жылдамдық.
H) Көлем.
$$$ 43
геометриялық мағынасы:
A) & Қисық сызықты трапецияның ауданы.
B) Нүкте.
C) Түзу.
D) Жазықтық.
E) Дөңгелек.
F) Үдеу.
G) Жылдамдық.
H) Көлем.
$$$ 44
y=4-x2, y=0 сызықтарымен шектелген фигураның ауданын тап:
A) & 32/3.
B) 15/7.
C) 10.
D) &.
E) 28/3.
F) & 
.
G) 5.
H) 3.
$$$ 45
болатындай А және В сандарын тап:
A) & A = 1, B = -1.
B) A = 1, B = 1.
C) A = -1, B = 1.
D) & A = 20, B = -1.
E) A = -1, B = -2.
F) A = -1, B = -1.
G) A = 2, B = 1.
H) 1.
$$$ 46
сызықтарымен шектелген фигураның ауданын тап:
A) & 9/2.
B) 2/9.
C) 5/7.
D) & (2/9)-1.
E) 1.
F) 8.
G) & 4,5.
H) 4.
$$$ 47
функциясы үшін 
- ті тап:
A)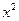 
.
B) & 
.
C) 
.
D) 
.
E) &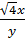 
.
F) 0.
G) 1.
H) 2.
$$$ 48
Егер 
болса, 
тап:
A) 
.
B)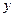 
.
C) 0.
D) & 
.
E) 
.
F) & 
.
G) 1.
H) 2.
$$$ 49
Егер беттің теңдеуі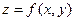 
түрінде берілсе, онда 
нүктесінде жанама жазықтығының теңдеуі мына түрде болады:
A) & 
.
B) 
.
C) 
.
D) 
.
E) 
.
F) .
G) 1.
H) 2.
$$$ 50
Егер беттің теңдеуі 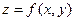түрінде берілсе, онда нүктесіндегі нормаль жазықтығының теңдеуі мына түрде болады:
A) .
B) & .
C) .
D) .
E) .
F) .
G) 1.
H) 2.
$$$ 51
берілсе, 
тап:
A) 
.
B) & 
.
C) 
.
D) 
.
E) 
.
F) .
G) 1.
H) 2.
$$$ 52
берілсе, тап:
A) .
B) .
C) .
D) & .
E) .
F) .
G) 1.
H) 2.
$$$ 53
берілсе, 
тап:
A) 7.
B) 3.
C) & 
.
D) 5.
E) & 
.
F) & 
.
G) 1.
H) 9.
$$$ 54
берілсе, 
тап:
A) 6.
B) 3.
C) 4.
D) & 5.
E) & 10- 
.
F) 2.
G) 1.
H) &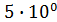 
.
$$$ 55
Меншіксіз интегралды есептеңіз 
:
A) 
.
B) 
.
C) & 
.
D) 
.
E) 
.
F) .
G) 1.
H) 2.
$$$ 56
Сандық қатар 
жинақталады дейміз, егер:
A) 
.
B) 
.
C) &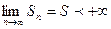 
.
D) 
.
E) 
.
F) .
G) 1.
H) 2.
$$$ 57
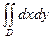есептеңіз, мұнда 
:
A) & 40.
B) & 1.
C) 5.
D) 6.
E) & 70.
F) -1.
G) lne.
H) -2.
$$$ 58
интегралын есептеңіз:
A) 9.
B) 5.
C) & 6.
D) 8.
E) & 2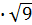 
.
F) .
G) & 
.
H) 7.
$$$ 59
облысы бойынша дененің көлемі келесі формула бойынша есептеледі:
A) 
.
B) & 
.
C) 
.
D) 
.
E)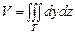 
.
F) .
G) 1.
H) 2.
$$$ 60
c ={1,1,2} және d ={2,1,0} векторларының скаляр көбейтіндісін табыңыз:
A) {2,1,0}.
B) & 3.
C) -2.
D) & 3 lne.
E) & 
.
F) 1.
G) 6.
H) 0.
$$$ 61
Ортогональ векторларды анықтаныз:
A) & c={-1,0,2}, d={0,6,0}.
B) c={1,-1,3}, d={1,2,0}.
C) c={0,1,3}, d={1,4,-2}.
D) & c={1,1,3}, d={1,2,-1}.
E) c={1,1,3}, d={4,0,1}.
F) & c={0,1,2}, d={1,4,-2}.
G) c={1,1,3}, d={1,4,-2}.
H) c={2,3,3}, d={1,4,-2}.
$$$ 62
Қандай векторлар коллинеар:
A) c={3,-1,0}, d={6,0,2}.
B) c={-1,2,-3}, d={2,4,6}.
C) & c={-2,1,-3}, d={4,-2,6}.
D) c={2,8,6}, d={1,-4,3}.
E) c={1,-3,0}, d={2,6,2}.
F) c={2,1,3}, d={4,-2,6}.
G) & c={2,-1,3}, d={4,-2,6}.
H) c={-2,1,-3}, d={-4,-2,-6}.
$$$ 63
c={2,4,4} және d={2,1,2} векторларының арасындағы бұрыштың cosa табыңыз:
A) cos a =0.
B) & cos a =8/9.
C) cos a =-8/9.
D) cos a =1/2.
E) & cos a =23/32.
F) cos a =-1/5.
G) cos a =1/3.
H) cos a =1.
$$$ 64
М нүктесі АВ кесіңдісінің ортасы, А =(2, 7, 6) М =(3, 1, 7). В нүктесінің координаталары қандай:
A) & B=(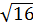
, -5, 
.
B) В=(4, 3, 0).
C) В=(-1, -5, 8).
D) В=(-2, 3, 7).
E) & В=(4, -5, 8).
F) В=(0, 2, 6).
G) В=(4, 3, 8).
H) & B=(
.
$$$ 65
М (1,1) нүктесінен 3 х +4 у -2=0 түзуіне дейінгі ара қашықтықты табыңыз:
A) 6.
B) 2.
C) 0.
D) & 1.
E) & 50.
F) 3.
G) 4.
H) & lne.
$$$ 66
М 1(2, -5) және М 2 (3, 2) нүктелері арқылы өтетін түзудің бұрыштық коэффициенті қандай:
A) –1.
B) & 
.
C) 3.
D) 0,5.
E) & 7.
F) -3.
G) & 14- .
H) -0,5.
$$$ 67
Төмендегі векторлардың қайсысы 3 х - у +2 z -5=0 жазықтығының нормаль векторы болады:
A) 
.
B) & 
.
C)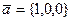 
.
D) 
.
E) 
.
F) 0.
G) 1.
H) 2.
$$$ 68
Төмендегі сандардың қайсысы эллипстің эксцентриситеті бола алады:
A) & 0,2.
B) 1.
C) 6.
D) & 0,5.
E) –0,3.
F) 
.
G) 5.
H) & 1/5.
$$$ 69
Эллипстің кіші жарты осі 24, ал фокустар қашықтығы 2 с =20. Эллипстің үлкен жарты осін табыңыз:
A) 56.
B) 30.
C) & 26.
D) 32.
E) & 
.
F) 25.
G) & 
.
H) 24.
$$$ 70
гиперболасының нақты жарты өсін табыңыз:
A) 4.
B) 36.
C) & 
.
D) & 6.
E) 2.
F) & 12- 
.
G) 9.
H) 3.
$$$ 71
А (2,-3) және В (-1,7) нүктелерінің ара қашықтығын табыңыз:
A) -3.
B) & 5.
C) 2.
D) 0.
E) & .
F) & 10- .
G) -5.
H) -2.
$$$ 72
векторының ұзындығын табыныз:
A) 0.
B) –7.
C) & 7.
D) 9.
E) –1.
F) & .
G) 2.
H) & 14- .
$$$ 73
Р- ның қандай мәнінде 
түзуі 
түзуіне параллель болады:
A) 1.
B) & 2.
C) 3.
D) -3.
E) & .
F) -1.
G) -2.
H) & log 24.
$$$ 74
Келесі анықтауышты есепте 
:
A) 2.
B) & 1.
C) -1.
D) & 100.
E) -2.
F) 5.
G) & lne.
H) 3.
$$$ 75
Келесі анықтауышты есепте 
:
A) -40.
B) 0.
C) & 40.
D) 49.
E) 1.
F) 7..
G) & 
.
H) & 40 lne.
$$$ 76
Келесі анықтауыш үшін М12 - минорды есепте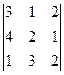 
:
A) & 7.
B) –7.
C) 0.
D) 1.
E) –1.
F) & .
G) 2.
H) & 14- .
$$$ 77
× 
матрицалардың көбейтіндісін есепте:
A) & 
.
B) 
.
C)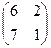 
.
D) 
.
E) 
.
F) .
G) 1.
H) 2.
$$$ 78
сызықтық тендеулер жүйесін шешініз:
A) & x= , y= -1.
B) x=1, y=3.
C) x=1, y=-3.
D) x=-3, y=1.
E) & x=3, y=-1.
F) x=-1, y=-3.
G) x= , y= 1.
H) & x=3, y=- lne.
$$$ 79
А квадрат матрицасы ерекше емес деп аталады, егер:
A) detA=0.
B) detA=1.
C) & detA≠0.
D) detA≠1.
E) detA>1.
F) .
G) 1.
H) 2.
$$$ 80
Егер анықтауыштың екі жолын орындарымен ауыстырсақ, онда:
A) & Анықтауыштың таңбасы өзгереді.
B) Анықтауыштың мәні нольге тең.
C) Анықтауыштың таңбасы өзгермейді.
D) Анықтауыштың мәні өзгермейді.
E) Анықтауыштың мәні бірге тең.
F) 5.
G) 1.
H) 2.
$$$ 81
анықтуышы үшін А13 алгебралық толықтауышын есептеңіз:
A) & .
B) -5.
C) -8.
D) & 5.
E) 0.
F) -2.
G) & 5 lne.
H) 1.
$$$ 82
+ 
матрицалардың қосындысын есептеніз:
A) 
.
B) 
.
C) 
.
D) &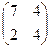 
.
E) 
.
F) 
.
G) & 
.
H) & 
.
$$$ 83
жүйесін шешу үшін Крамер формуласын көрсетіңіз:
A) 
; 
.
B) & 
; 
.
C) 
.
D) 
.
E) 
.
F) .
G) 1.
H) 2.
$$$ 84
А квадрат матрицасы ерекше деп аталады, егер:
A) & detA=0.
B) detA=1.
C) detA≠0.
D) detA≠1.
E) & detA= ln 1.
F) detA=2.
G) detA=-1.
H) & detA= lne -100.
$$$ 85
Екі жолы өзара пропорционал анықтауыш:
A) & Нөлге тең.
B) Нөлге тең емес.
C) 1-ге тең.
D) –1 – ге тең.
E) 2- ге тең.
F) e.
G) 1.5.
H) 2.5.
$$$ 86
Бернулли формуласы:
A) 
.
B) 
.
C) 
.
D) & 
.
E) 
.
F) 
.
G) 1.
H) 2.
$$$ 87
Х дискретті кездейсоқ шаманың математикалық күтімінің формауласы:
A)
