При изучении дисциплины «Математика» необходимо выполнить две контрольные работы №1 и №2. Вариант каждой задачи выбирается по двум последним цифрам номера студенческого билета. Предпоследняя цифра обозначается буквой M, последняя буквой N. Например, для студенческого билета номер 147 M = 4, N = 7.
КОНТРОЛЬНАЯ РАБОТА 1
Задача 1
Даны векторы 
и 
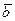. Найти вектор 
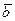= + , скалярное произведение ( · 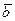) и модули этих векторов, где = (1, М + 4, -1, N – 5), 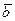= (-М + 5, -1, 5 - N, 2).
Задача 2
Найти значение матрицы D = A · B – C 2 и вычислить ее определитель, если даны матрицы:
A = 
, B = 
, C = 
.
Задача 3
Пользуясь формулами Крамера и методом Гаусса решить систему из трех уравнений:
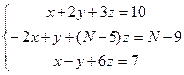
Задача 4
a) Найти точку пересечения прямых 
и 
b) Найти уравнение прямой, проходящей через точку (M +1; N +1) и перпендикулярно к прямой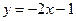 
c) Найти уравнение прямой параллельной к прямой и проходящей через точку (M; N)
d) Какая кривая описывается уравнением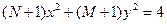 
? Написать каноническое уравнение этой кривой.
Задача 5
Найти производные функций:
а) у = (М +N+5) x M+N+2;
b) у = ln(x + N) cos(M + 2) x - e(N+1) x tg(M + 2) x;
c) y =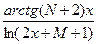 
;
d) y = sin[ln(3 x + N +2)] - arctg[cos(M +3) x ].
Задача 6
Найти вторую производную функции: у = 
.
Задача 7
Разложить по формуле Тейлора в окрестности точки х = 0 до членов порядка х 2 функцию 
и найти ее приближенное значение при х = 0,1.
Задача 8
Исследовать функции и построить их графики:
a) 
b) 
Задача 9
Найти неопределенные интегралы:
d) 
;
e)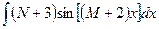 
;
c)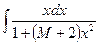 
;
d) 
КОНТРОЛЬНАЯ РАБОТА 2
Задача 1
Найти определенные интегралы:
a)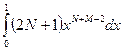 
;
b)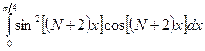 
;
с) найти площадь верхней полуволны синусоиды у = sin (М + N + 3) х.
Задача 2
Найти первые частные производные функций.
a) z = x N+1(cos y)M+2;
b) z = (e xy + (N +2) xy)2;
с) z = arctg(xy + M +1);
d) u = [(N+2) x + 2 y + (M+3) z ]2.
Задача 3
Найти градиент функции в точке (хо,уо):
a) z = 2 x N+2 +3 y 10-M, x 0 = y 0 = 1
b) z = cos((M+2) x + (11-N) y), x 0 = y 0 = π/2
Задача 4
Исследовать на экстремум функцию z = (х - М -1)2 - ху + (у + N +1)2.
Задача 5
Найти общее решение дифференциальных уравнений и проверить правильность найденных решений дифференцированием:
a) 
;
b)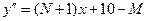 
;
c) 
Задача 6
Найти решения дифференциальных уравнений с разделяющимися переменными:
a) (y +11-N) dx = (x -M-1) dy
b) (y +10-M) dx + 2 x N+1 dy = 0
c) 
Задача 7
Найти решения линейных однородных уравнений с постоянными коэффициентами:
a) (М + 2) у' + (12 - N) y = 0;
b) у" + 2 
у' + (N + 1) у = 0;
c) у" -2 
у' + (М + 10) у = 0 с условиями у = 0, у' = 1 при х = 0;
d) y"- 2 
y' + (N+3) y = 0.
Задача 8
Найти решения линейных неоднородных уравнений с постоянными коэффициентами в виде суммы общего решения однородного уравнения и произвольного частного решения неоднородного уравнения:
a) y' + (N + 2) y =M+3, у = 0 при х = 0;
b) у" - 2 
у' + (N + 1) у = М + 5.
ВОПРОСЫ К ЭКЗАМЕНУ
1. Вектор в прямоугольной n-мерной системе координат. Сложение векторов и умножение вектора на число.
2. Скалярное произведение векторов. Модуль вектора.
3. Матрицы. Виды матриц. Действия над матрицами.
4. Определители второго и третьего порядков. Свойства определителей.
5. Миноры и алгебраические дополнения. Разложение определителя по строке и столбцу. Метод треугольников.
6. Обратная матрица.
7. Система n линейных уравнений с n неизвестными. Запись и решение в матричном виде.
8. Формулы Крамера.
9. Метод Гаусса. Теорема Кронекера – Капелли.
10. Прямоугольная система координат на плоскости.
11. Прямая на плоскости. Угловой коэффициент. Уравнения прямой с заданным угловым коэффициентом, проходящей через две точки, уравнение в отрезках.
12. Угол между прямыми на плоскости. Признаки параллельности и перпендикулярности прямых. Общее уравнение прямой на плоскости, геометрический смысл его коэффициентов.
13. Кривые второго порядка: окружность, эллипс, гипербола, парабола.
14. Окрестности точек. Определение предела функции.
15. Бесконечно малые и бесконечно большие функции и их свойства.
16. Предел суммы, разности, произведения и частного.
17. Первый замечательный предел. Функции, эквивалентные в точке
18. Второй замечательный предел. Функции, эквивалентные в точке
19. Непрерывность функции в точке. Непрерывность суммы, разности, произведения, частного.
20. Односторонняя непрерывность. Классификация точек разрыва функции.
21. Производная, её геометрический смысл. Связь между дифференцируемостью и непрерывностью.
22. Таблица производных. Правила дифференцирования. Уравнение касательной к графику функции.
23. Производные высших порядков. Логарифмическая производная.
24. Дифференциал. Геометрический смысл дифференциала.
25. Применение дифференциала в приближенных вычислениях.
26. Признаки монотонности функции.
27. Поиск экстремумов функции.
28. Выпуклость, вогнутость, точки перегиба.
29. Асимптоты графика функции.
30. Формула Тейлора. Остаточный член.
31. Разложение в ряд Тейлора функций еx, sin(x), cos(x), (1 + х)n.
32. Первообразная и неопределенный интеграл. Свойства неопределенного интеграла.
33. Замена переменной при интегрировании. Интегрирование по частям.
34. Понятие определенного интеграла. Формула Ньютона - Лейбница.
35. Интегрирование по частям и замена переменной в определенном интеграле.
36. Приложения определенного интеграла.
37. Функция многих переменных. Частные производные. Частные производные высших порядков.
38. Линии уровня и градиент функции Производная по направлению.
39. Экстремум функций двух переменных, необходимые и достаточные условия.
40. Понятие дифференциального уравнения. Частное и общее решения.
41. Уравнения первого порядка с разделяющимися переменными.
42. Линейные однородные уравнения второго порядка с постоянными коэффициентами. Общее и частное решение.
43. Линейные неоднородные уравнения второго порядка. Отыскание частного решения по виду правой части уравнения.
44. Числовой ряд, частичная сумма и сумма ряда. Признаки сходимости: сравнения и Даламбера.
45. Абсолютная и условная сходимость. Признак сходимости Лейбница.
46. Сходимость степенных рядов. Интервал и радиус сходимости степенного ряда.
