ОГЛАВЛЕНИЕ
ОБЩИЕ ОРГАНИЗАЦИОННО-МЕТОДИЧЕСКИЕ УКАЗАНИЯ.. 3
ТЕМАТИЧЕСКИЙ ПЛАН.. 4
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ... 6
СОДЕРЖАНИЕ И МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ИЗУЧЕНИЮ ТЕМ ДИСЦИПЛИНЫ 7
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО РЕШЕНИЮ ЗАДАЧ. 15
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К КОНТРОЛЬНЫМ РАБОТАМ... 29
КОНТРОЛЬНАЯ РАБОТА 1. 29
КОНТРОЛЬНАЯ РАБОТА 2. 30
ВОПРОСЫ К ЭКЗАМЕНУ.. 32
ОБЩИЕ ОРГАНИЗАЦИОННО-МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Настоящие методические указания составлены на основе ФГОС ВПО по направлению 040400.62 «Социальная работа», утвержденного 8 декабря 2009 г. и рабочего учебного плана данного направления.
Целью дисциплины «Математика» является подготовка в соответствии с квалификационной характеристикой бакалавра и рабочим учебным планом направления подготовки 040400.62 Социальная работа.
Задачи изложения и изучения дисциплины – дать необходимые знания по основам математики для решения задач в профессиональной деятельности.
Процесс изучения дисциплины «Математика» направлен на формирование элементов следующих компетенций в соответствии с ФГОС ВПО по направлению подготовки 040400.62 Социальная работа. Профиль: социальная защита и социальное обслуживание семей и детей:
а) общекультурных (ОК):
– владеть культурой мышления, способен к обобщению, анализу, восприятию информации, постановке цели и выбору путей ее достижения (ОК-1);
– уметь логически верно, аргументировано и ясно строить устную и письменную речь (ОК-2);
– использовать в профессиональной деятельности основные законы естественнонаучных дисциплин, в том числе медицины, применять методы математического анализа и моделирования, теоретического и экспериментального исследования (ОК-10).
В результате изучения дисциплины студент должен:
Знатьосновы аналитической геометрии, линейной алгебры, дифференциальных и интегральных исчислений;
Уметь использовать математические модели явлений и процессов в социальной работе;
Владетьматематическими методами исследования в социальной работе.
Для изучения данной дисциплины студентам необходимо усвоение математики в объеме курса общеобразовательного учреждения. Усвоение других дисциплин не требуется.
ТЕМАТИЧЕСКИЙ ПЛАН
Общая трудоемкость дисциплины составляет
5 зачетных единиц, 180 часов.
| № п\п | Содержание разделов (модулей), тем дисциплины | Количество часов, выделяемых на виды учебной подготовки | ||
| Лекции | ПР | СР | ||
| 1 семестр | ||||
| Линейная алгебра с элементами аналитической геометрии. | ||||
| Вектор в декартовых координатах. Операции над векторами, свойства операций. Матрицы. Основные операции над матрицами. Определители и их свойства. Вычисление определителей. Решение систем линейных алгебраических уравнений. | ||||
| Прямая на плоскости. Кривые второго порядка. Уравнение плоскости и прямой в пространстве. | ||||
| Функции. Предел и непрерывность. | ||||
| Понятие множества и функции. Предел функции. Бесконечно большие и бесконечно малые функции. Теоремы о пределах. Замечательные пределы. Непрерывность функции в точке и на множестве. Точки разрыва и их классификация. | ||||
| Дифференциальное исчисление. | 0,5 | 0,5 | ||
| Производная и ее геометрический смысл. Таблица производных основных элементарных функций. Правила дифференцирования. Производная сложной функции. Производные высших порядков. Касательная и нормаль к плоской кривой. Понятие дифференциала и его геометрический смысл. Исследование функций и построение графиков с помощью производной. | 0,5 | 0,5 | ||
| Первообразная и интеграл | 1,5 | 1,5 | ||
| Первообразная и неопределенный интеграл, основные свойства. Таблица интегралов. Методы интегрирования. | ||||
| Определенный интеграл и его свойства. Геометрический смысл интеграла. Формула Ньютона-Лейбница. Приложения определенного интеграла. | 0,5 | 0,5 | ||
| Функции нескольких переменных. | 0,5 | 0,5 | ||
| Частные производные ФНП. Градиент и производная по направлению. Формула Тейлора для функции двух переменных. Экстремумы функций нескольких переменных. Необходимые и достаточные условия. | 0,5 | 0,5 | ||
| Дифференциальные уравнения. | 1,5 | 1,5 | ||
| Дифференциальные уравнения первого порядка. Частное и общее решения. Задача Коши. Дифференциальные уравнения с разделяющимися переменными. Однородные дифференциальные уравнения первого порядка. Линейные дифференциальные уравнения первого порядка. Уравнения Бернулли. | ||||
| Линейные дифференциальные уравнения с постоянными коэффициентами. Характеристическое уравнение. Общее решение. | 0,5 | 0,5 | ||
| Ряды. | ||||
| Числовые ряды. Необходимый признак сходимости ряда. Знакопостоянные ряды, признаки сходимости. Знакочередующиеся ряды, их абсолютная и условная сходимости. | 0,5 | 0,5 | ||
| Степенные ряды. Центр и радиус сходимости степенного ряда. Ряды Тейлора и Маклорена. Разложение основных элементарных функций. | 0,5 | 0,5 | ||
| Всего в 1-м семестре: | ||||
| Итого: |
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
Основная
1. В.С.Щипачев. Задачник по высшей математике: Учеб. Пособие для вузов. - М., Высшая школа, 2002. – 304с.: ил.
2. Общий курс высшей математики для экономистов. Учеб. пособие под ред. В.И.Ермакова - М.: Инфра,2006-33с
3. Сборник задач по высшей математике для экономистов: Учеб. пособие под ред. В.И.Ермакова - М.: Инфра,2006-516с
Дополнительная
4. Кремер Н.Ш. и др. Высшая математика для экономистов / Кремер Н.Ш., Путко Б.А., Тришин И.М., Фридман М.Н.- М.: Банки и биржи, 2000.- 439 с.
5. Лунгу К.Н., Норин В.П., Письменный Д.Т., Шевченко Ю.А. Сборник задач по высшей математике. В 2 ч. / под ред. С.Н. Фетина. - М.: Айрис-пресс, 2006. – 592 с.
6. Письменный Д.Т. Конспект лекций по высшей математике: полный курс. - М.: Айрис-пресс, 2006. – 592 с.
СОДЕРЖАНИЕ И МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ИЗУЧЕНИЮ ТЕМ ДИСЦИПЛИНЫ
Тема: Линейная алгебра
Вектор в декартовых координатах. Операции над векторами, свойства операций. Линейная зависимость и независимость векторов.
Матрицы, виды матриц. Основные операции над матрицами. Ранг матрицы. Обратная матрица. Определители и их свойства. Миноры и алгебраические дополнения. Системы линейных алгебраических уравнений (СЛАУ). Формулы Крамера. Решение систем линейных уравнений методом Гаусса. Матричный способ решения систем линейных уравнений.
Цель: освоить основные понятия: вектора, матрицы и определителя; закрепить навыки выполнения операций над матрицами и векторами; закрепить навыки вычисления определителей и систем линейных алгебраических уравнений.
Методические рекомендации по изучению темы: используйте образцы решения примеров, приведенных в учебной литературе, а также решите задачи № 1, №2, №3 из контрольной №1; при вычислении определителей используйте их свойства; при решении вопроса о наличии решения СЛАУ удобнее находить ранг матрицы.
Рекомендуемая литература:
Основная: [1]-[3].
Дополнительная: [4] – [6]
Вопросы и задания для самопроверки:
1. Приведите определение матрицы, определителя и вектора.
2. Сформулируйте основные операции над матрицами.
3. Перечислите свойства определителей.
4. Что называется минором, алгебраическим дополнением элемента матрицы?
5. Приведите методы вычисления определителей второго и третьего порядка.
6. Сформулируйте алгоритм нахождения обратной матрицы.
7. Дать определение СЛАУ.
8. Сформулируйте основные методы решения СЛАУ.
Тема: Аналитическая геометрия на плоскости и в пространстве
Прямая на плоскости. Виды уравнений прямой на плоскости. Условия параллельности и перпендикулярности. Угол между прямыми. Кривые второго порядка: окружность, эллипс, гипербола, парабола. Уравнение плоскости и прямой в пространстве. Взаимное расположение прямых и плоскостей.
Цель: освоить основные понятия аналитической геометрии на плоскости и в пространстве; закрепить навыки построения прямых на плоскости и кривых второго порядка.
Методические рекомендации по изучению темы: используйте образцы решения примеров, приведенных в учебной литературе, а также решите задачу № 4 из контрольной №1; при построении кривых второго порядка рекомендуется приводить их уравнения к каноническому виду.
Рекомендуемая литература:
Основная: [1]-[3].
Дополнительная: [4] – [6]
Вопросы для самопроверки:
1. Сформулируйте основные понятия системы координат на плоскости.
2. Как осуществляется решение основных задач на плоскости: нахождение расстояния между двумя точками, деление отрезка в заданном отношении.
3. Приведите различные виды уравнения прямой на плоскости.
4. Запишите формулы для нахождения угла между двумя прямыми, признаки параллельности и перпендикулярности прямых, расстояние от точки до прямой.
5. Запишите канонические уравнения кривых второго порядка: окружность, эллипс, гипербола, парабола.
6. Основные виды уравнений плоскости в пространстве: общее, проходящей через три точки, проходящей через точку, перпендикулярно заданному вектору, в отрезках, нормальное уравнение.
7. Как найти угол между двумя плоскостями и расстояние от точки до плоскости?
Тема: Функция. Предел и непрерывность функции.
Понятие множества. Основные операции над множествами. Функция. Основные свойства функций. Элементарные функции и их графики. Предел последовательности и его свойства. Предел функции. Бесконечно большие и бесконечно малые функции. Теоремы о пределах. Замечательные пределы. Непрерывность функции в точке и на промежутке. Точки разрыва и их классификация. Теоремы о непрерывных функциях. Свойства функций, непрерывных на отрезке.
Цель: освоить основные понятия теории пределов, теории множеств; закрепить навыки вычисления пределов и определения непрерывности функции.
Методические рекомендации по изучению темы: используйте образцы решения примеров, приведенных в учебной литературе; при вычислении пределов помните о свойствах бесконечно больших и бесконечно малых величин.
Рекомендуемая литература:
Основная: [1]-[3].
Дополнительная: [4] – [6]
Вопросы и задания для самопроверки:
1. Дайте определение функции.
2. Перечислите способы задания функции.
3. Сформулируйте характеристики функции: область определения, множество значений, четность, периодичность, монотонность, промежутки знакопостоянства, точки экстремума.
4. Сформулируйте определение предела функции в точке, односторонних пределов, предела функции на бесконечности.
5. Дайте определение бесконечно малых и бесконечно больших функций и перечислите их свойства.
6. Сформулируйте основные теоремы о пределах.
7. Запишите первый и второй замечательные пределы и их следствия.
8. Перечислите основные способы вычисления пределов.
9. Дать определение непрерывности функции в точке, на интервале, на отрезке.
10. Как классифицируются точки разрыва функции?
Тема: Дифференциальное исчисление.
Производная и ее геометрический смысл. Таблица производных элементарных функций. Правила дифференцирования. Теоремы о производных. Производная сложной функции. Производные высших порядков. Касательная и нормаль к плоской кривой. Понятие дифференциала и его геометрический смысл. Применение дифференциала для приближенных вычислений. Исследование функций и построение графиков с помощью производной.
Цель: освоить основные понятия дифференциального исчисления; закрепить навыки нахождения производных и применение производных и дифференциалов.
Методические рекомендации по изучению темы: используйте образцы решения примеров, приведенных в учебной литературе, а также решите задачи №5, №6, №7, №8 из контрольной №1; при нахождении производных и дифференциалов необходимо использовать таблицу производных и правила дифференцирования. Исследование функций необходимо проводить в соответствии с планом исследования.
Рекомендуемая литература:
Основная: [1]-[3].
Дополнительная: [4] – [6]
Вопросы и задания для самопроверки:
1. Дать определение производной.
2. Сформулировать правила вычисления производной.
3. Сформулируйте основные теоремы дифференцирования.
4. Сформулируйте определения и теоремы об основных характеристиках функции: возрастание и убывание, максимум и минимум, наибольшее и наименьшее значение, выпуклость и вогнутость.
5. Как найти асимптоты графика функции?
6. Приведите схему полного исследования функции.
7. Как применяется формула Тейлора?
Тема: Неопределенный интеграл.
Первообразная и неопределенный интеграл, основные свойства. Таблица интегралов. Методы интегрирования: непосредственное интегрирование; замена переменной; интегрирование по частям; тригонометрические подстановки. Интегрирование дробно-рациональных функций.
Цель: освоить основные понятия интегрального исчисления; закрепить навыки вычисления неопределенных интегралов.
Методические рекомендации по изучению темы: используйте образцы решения примеров, приведенных в учебной литературе, а также решите задачу № 9 из контрольной №1; при вычислении неопределенного интеграла необходимо использовать таблицу первообразных и свойства интегралов, а также помнить, что при замене переменной необходимо после вычисления интеграла вернуться к исходной переменной.
Рекомендуемая литература:
Основная: [1]-[3].
Дополнительная: [4] – [6]
Вопросы и задания для самопроверки:
1. Сформулируйте определение неопределенного интеграла.
2. В чем заключается метод непосредственного интегрирования?
3. Как осуществляется метод интегрирования заменой переменной?
4. Приведите формулу интегрирования по частям.
Тема: Определенный интеграл.
Понятие интегральной суммы. Определенный интеграл и его свойства. Геометрический смысл интеграла. Формула Ньютона-Лейбница. Замена переменной и интегрирование по частям в определенном интеграле. Понятие несобственного интеграла. Приложения определенного интеграла: вычисление площадей фигур.
Цель: освоить основные понятия интегрального исчисления; закрепить навыки вычисления определенных интегралов и приложения к нахождению площади криволинейной трапеции, объемов тел вращения и длины дуги кривой.
Методические рекомендации по изучению темы: используйте образцы решения примеров, приведенных в учебной литературе, а также решите задачу 1 из контрольной работы №2; при вычислении определенного интеграла необходимо использовать таблицу первообразных и свойства интегралов также как и при вычислении неопределенных интегралов. При использовании метода интегрирования – замена переменной, достаточно перейти к новым пределам интегрирования и тогда после нахождения интеграла возвращаться к исходным переменным не требуется.
Рекомендуемая литература:
Основная: [1]-[3].
Дополнительная: [4] – [6]
Вопросы и задания для самопроверки:
1. Показать, что определенный интеграл есть предел интегральной суммы.
2. Пояснить геометрический и физический смысл определенного интеграла.
3. Сформулируйте формулу Ньютона-Лейбница и основные свойства определенного интеграла.
4. Какие методы интегрирования определенного интеграла и в чем отличие от таких же методов для неопределенного интеграла?
5. Как применяются определенные интегралы?
Тема: Функции нескольких переменных.
Функции нескольких переменных (ФНП). Способы задания. Линии уровня.
Частные производные ФНП. Частные дифференциалы и полный дифференциал ФНП. Частные производные высших порядков. Градиент и производная по направлению. Формула Тейлора для функции двух переменных. Экстремумы функций нескольких переменных. Необходимые и достаточные условия экстремума.
Цель: освоить основные понятия функции многих переменных; закрепить навыки нахождения производных и дифференциалов.
Методические рекомендации по изучению темы: используйте образцы решения примеров, приведенных в учебной литературе, а также решите задачи №2, №3, №4 из контрольной работы №2; при нахождении частных производных следует помнить, что если по одной переменной функцию дифференцируем, то остальные переменные этой функции считаются постоянными.
Рекомендуемая литература:
Основная: [1]-[3].
Дополнительная: [4] – [6]
Вопросы и задания для самопроверки:
1. Дать основные понятия ФНП.
2. Сформулировать определение предела функции и непрерывности функции двух переменных
3. Как находятся частные производные первого и второго порядка?
4. Что такое полный дифференциал?
5. Сформулируйте необходимое и достаточное условия экстремума.
Тема: Ряды.
Числовые ряды. Основные понятия и определения. Необходимый признак сходимости числового ряда. Знакопостоянные ряды и их признаки сходимости: Даламбера, интегральный признак Коши, сравнения. Знакочередующиеся ряды, их абсолютная и условная сходимости. Степенные ряды. Интервал и радиус сходимости степенного ряда. Разложение функций в степенные ряды Тейлора и Маклорена.
Цель: освоить основные понятия темы ряды; закрепить навыки исследования рядов на сходимость.
Методические рекомендации по изучению темы: используйте образцы решения примеров, приведенных в учебной литературе; составьте краткий конспект изучаемой темы.
Рекомендуемая литература:
Основная: [1]-[3].
Дополнительная: [4] – [6]
Вопросы и задания для самопроверки:
1. Что называется числовым рядом?
2. Сформулируйте необходимый признак сходимости числового ряда.
3. Какие достаточные признаки сходимости числовых рядов вы знаете?
4. Какие числовые ряды называются абсолютно и условно сходящимися?
5. Как найти интервал и радиус сходимости степенного ряда?
Тема: Дифференциальные уравнения.
Дифференциальные уравнения первого порядка. Частное и общее решения. Задача Коши. Дифференциальные уравнения с разделяющимися переменными. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами. Характеристическое уравнение. Нахождение частных решений неоднородных уравнений с постоянными коэффициентами.
Цель: освоить основные понятия темы дифференциальные уравнения; закрепить навыки решения основных видов дифференциальных уравнений. Методические рекомендации по изучению темы: используйте образцы решения примеров, приведенных в учебной литературе, а также решите задачи №5, №6, №7 и №8 из контрольной работы №2; при решении дифференциальных уравнений первого порядка с разделяющимися переменными необходимо следить за появлением особых решений, так как возможна их потеря в результате преобразования уравнений.
Рекомендуемая литература:
Основная: [1]-[3].
Дополнительная: [4] – [6]
Вопросы и задания для самопроверки:
1. Дать определение дифференциального уравнения.
2. Что значит решить задачу Коши?
3. Как решаются дифференциальные уравнения первого порядка с разделяющимися переменными?
4. Что такое характеристическое уравнение?
5. Как найти общее и частное решение линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами?
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО РЕШЕНИЮ ЗАДАЧ.
Задача 1
Даны векторы  и
и  . Найти вектор
. Найти вектор  =
=  +
+  , скалярное произведение (
, скалярное произведение ( ·
·  ) и модуль вектора
) и модуль вектора  , где
, где  = (1; 4; -1; -5),
= (1; 4; -1; -5),  = (5; -1; 5; 2).
= (5; -1; 5; 2).
Решение:
Вектор  находится как сумма двух векторов
находится как сумма двух векторов  и
и  . Для того чтобы найти сумму двух векторов заданных координатами необходимо сложить их соответствующие координаты.
. Для того чтобы найти сумму двух векторов заданных координатами необходимо сложить их соответствующие координаты.
 =
=  +
+  = (1; 4; -1; -5) + (5; -1; 5; 2) = (6; 3; 4; -3).
= (1; 4; -1; -5) + (5; -1; 5; 2) = (6; 3; 4; -3).
Скалярное произведение векторов – это число, полученное как сумма произведений соответствующих координат векторов.
 ·
·  = 1·5 + 4·(-1) + (-1)·5 + (-5)·2 = -14
= 1·5 + 4·(-1) + (-1)·5 + (-5)·2 = -14
Длина вектора находится по формуле:
 , где
, где  =
=  .
.
Тогда: 
Задача 2
Найти значение матрицы D = A · B – C2 и вычислить ее определитель, если даны матрицы:
A =  , B =
, B =  , C =
, C =  .
.
Решение:
Для того чтобы найти значение матрицы D, необходимо в первую очередь найти произведение матриц А и В. Операция умножения двух матриц возможна только в случае, если число столбцов первой матрицы равно числу строк второй матрицы, тогда 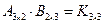 . Произведением матрицы
. Произведением матрицы  на матрицу
на матрицу  называется матрица
называется матрица  такая, что
такая, что  , где i = 1,.. m; k = 1,... p, то есть элемент i -й строки и k -го столбца матрицы произведения C равен сумме произведений элементов i -й строки матрицы A на соответствующие элементы k -го столбца матрицы B. Тогда произведение двух матриц A и B:
, где i = 1,.. m; k = 1,... p, то есть элемент i -й строки и k -го столбца матрицы произведения C равен сумме произведений элементов i -й строки матрицы A на соответствующие элементы k -го столбца матрицы B. Тогда произведение двух матриц A и B:


Аналогично находим С2 , как произведение матрицы С на саму себя, то есть:

Для того, чтобы найти разность двух матриц необходимо найти разность соответствующих элементов этих матриц:

Вычислим определитель матрицы D разложением по первой строке, так как первая строка содержит больше всего нулей:

Задача 3
Решить систему из трех уравнений

a) по формулам Крамера;
b) методом Гаусса.
Решение:
a) При решении системы с использованием формул Крамера необходимо составить определители. Обозначим ∆ - главный определитель системы (составляется из коэффициентов при переменных), а ∆i - дополнительные определители (составляются из главного путем замены i -того столбца коэффициентов на столбец свободных членов). Формулы:  , где i = 1,... n называются формулами Крамера.
, где i = 1,... n называются формулами Крамера.
Составим определители и вычислим их:
 18,
18,  54,
54, 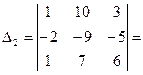 36,
36,  18. Значит,
18. Значит,  ,
,  ,
,  .
.
b) Процесс решения по методу Гаусса состоит из двух этапов. На первом этапе система приводится к ступенчатому виду с помощью элементарных преобразований расширенной матрицы системы. На втором этапе идет последовательное определение неизвестных из полученной ступенчатой системы.
Для решения данной системы уравнений составим расширенную матрицу системы из коэффициентов при переменных и столбца свободных членов. С помощью элементарных преобразований приведем ее к ступенчатому виду:


В результате исходная система преобразовалась к ступенчатой (восстановим запись системы из полученной ступенчатой матрицы): 
Решение данной системы: x = 3, y = 2, z = 1.
Задача 4
a) Найти точку пересечения прямых  и
и 
b) Найти уравнение прямой, проходящей через точку (1; 2) перпендикулярно к прямой 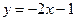
c) Найти уравнение прямой, параллельной к прямой  и проходящей через точку (2; 1)
и проходящей через точку (2; 1)
d) Какая кривая описывается уравнением  ? Написать каноническое уравнение этой кривой.
? Написать каноническое уравнение этой кривой.
Решение:
a) Задача о нахождении точки пересечения двух прямых сводится к отысканию точки, координаты которой являются решением системы двух уравнений с двумя неизвестными: 
Таким образом точка пересечения имеет координаты: 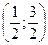
c) Уравнение прямой, проходящей через точку (x0; y0) имеет вид:
y –y0 = k (x – x0).
Для нахождения углового коэффициента k воспользуемся условием перпендикулярности двух прямых:  . Тогда искомое уравнение прямой:
. Тогда искомое уравнение прямой:  , где угловой коэффициент прямой:
, где угловой коэффициент прямой:  . Запишем полученное уравнение прямой в общем виде:
. Запишем полученное уравнение прямой в общем виде:  или x - 2 y + 3 = 0.
или x - 2 y + 3 = 0.
c) В данной задаче воспользуемся условием параллельности двух прямых: k1 = k2. Тогда уравнение искомой прямой:  , где угловой коэффициент прямой: k1 = k2 =2. Запишем полученное уравнение прямой в общем виде: 2 x – y – 3 = 0.
, где угловой коэффициент прямой: k1 = k2 =2. Запишем полученное уравнение прямой в общем виде: 2 x – y – 3 = 0.
d) Данная кривая является эллипсом. Каноническое уравнение эллипса:  . Приведем уравнение
. Приведем уравнение  к каноническому виду:
к каноническому виду:  . Тогда:
. Тогда:  .
.
Задача 5
Найти производные функций:
а) y = 2 x- 3/2
b) y = x2·cos (5 x+ 1) + 
c) y = ln (sin (5 x+ 1))
Решение:
Для нахождения производных функций необходимо воспользоваться таблицей производных и правилами дифференцирования.
а) Найдем производную функции y = 2 x- 3/2 . Для этого вынесем постоянный множитель за знак производной и воспользуемся формулой из таблицы производных:  . Получим:
. Получим: 
b) Найдем производную функции y = x2·cos (5x+1) +  . Для этого воспользуемся правилами дифференцирования:
. Для этого воспользуемся правилами дифференцирования:  ;
;  ;
;  и формулами из таблицы производных:
и формулами из таблицы производных:  ,
,  . Функция cos (5 x+ 1) является сложной функцией, где cos (5 x+ 1) = cos (u), u = 5 x+ 1. Тогда по правилу дифференцирования сложной функции
. Функция cos (5 x+ 1) является сложной функцией, где cos (5 x+ 1) = cos (u), u = 5 x+ 1. Тогда по правилу дифференцирования сложной функции  . Аналогично находится производная функций cos (3 x)и ln (4 x). Получим:
. Аналогично находится производная функций cos (3 x)и ln (4 x). Получим:  =
= 
c) Найдем производную функции y = ln (sin (5 x+ 1)). Данная функция является сложной, где y = ln (z), z = sin (u), u = 5 x+ 1. По правилу дифференцирования сложной функции получим  . Тогда:
. Тогда: 
Задача 6
Найти вторую производную функции: у =  .
.
Решение:
По определению:  .
.
Найдем производную первого порядка используя правила дифференцирования и формулу  . Получим:
. Получим:
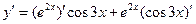 =
=  .
.
Тогда:  =
=  =
=  =
=  .
.
Задача 7
Разложить по формуле Тейлора в окрестности точки х = 0 до членов порядка х2 функцию 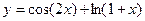 и найти ее приближенное значение при х = 0,1.
и найти ее приближенное значение при х = 0,1.
Решение:
Формула Тейлора в окрестности точки х = 0 имеет вид:
 ,
,
где n! = 1·2·3·4·….· n.
Для того, чтобы разложить заданную функцию до членов порядка х2, необходимо найти  ,
,  ,
,  . Найдем:
. Найдем:  ;
;  . Тогда:
. Тогда:  ,
,  ,
,  . Получим следующее разложение:
. Получим следующее разложение:  . Найдем приближенное значение функции при х = 0,1:
. Найдем приближенное значение функции при х = 0,1: 
Задача 8
Исследовать функцию и построить ее график: 
Решение:
Исследовать функцию и построить ее график: 
Решение:
Схема исследования функции:
1) Область определения функции, точки разрыва.
2) Интервалы возрастания и убывания функции.
3) Найти точки экстремума.
4) Интервалы выпуклости и вогнутости функции.
5) Найти точки перегиба.
6) Асимптоты графика функции.
На основании проведенного исследования строится график функции.
Область определения функции  – вся числовая ось, то есть
– вся числовая ось, то есть  . Значит, точек разрыва нет.
. Значит, точек разрыва нет.
Найдем интервалы монотонности и экстремумы функции, исследуя первую производную:  . Производная обращается в нуль при х = 0. При х < 0 производная положительная, а при x > 0 производная отрицательная. Это означает, что функция возрастает на
. Производная обращается в нуль при х = 0. При х < 0 производная положительная, а при x > 0 производная отрицательная. Это означает, что функция возрастает на  и убывает на
и убывает на  . В точке х = 0 функция имеет максимум.
. В точке х = 0 функция имеет максимум.
Чтобы определить интервалы выпуклости и точки перегиба, вычислим вторую производную функции:  . Вторая производная обращается в нуль при
. Вторая производная обращается в нуль при  . Тогда
. Тогда  и
и  . Вторая производная положительна на интервалах:
. Вторая производная положительна на интервалах:  , следовательно на этих интервалах функция вогнута. Вторая производная отрицательна на
, следовательно на этих интервалах функция вогнута. Вторая производная отрицательна на  , тогда функция на этом интервале выпукла. Точки
, тогда функция на этом интервале выпукла. Точки  и
и  - это точки перегиба функции.
- это точки перегиба функции.
Найдем асимптоты графика функции. Вертикальных асимптот нет, так как область определения  . Найдем наклонную асимптоту
. Найдем наклонную асимптоту  . Для этого найдем предел:
. Для этого найдем предел:  . Следовательно, наклонной асимптоты нет. Горизонтальная асимптота
. Следовательно, наклонной асимптоты нет. Горизонтальная асимптота  , где
, где  . Тогда y = 0.
. Тогда y = 0.
Для построения графика вычислим значения функции в найденных точках:  ,
,  .
.
Построим график функции:

Задача 9
Найти неопределенные интегралы:
a)  ;
;
b)  ;
;
c) 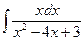 ;
;
d) 
Решение:
a) Для нахождения интеграла можно использовать свойства интегралов: интеграл от разности функций равен разности интегралов; постоянный множитель можно вынести за знак интеграла, а также формулу  .
.
 .
.
b) Данный интеграл не является табличным, поэтому для его нахождения можно применить замену переменной. Заменим 1 + 2 x 2 на t, то есть t = 1 + 2 x 2 . Тогда по правилу вычисления дифференциала  , следовательно
, следовательно  .
.
 =
= 
c) При вычислении интеграла от дробно-рациональной функции вида  можно в знаменателе подынтегральной функции выделить полный квадрат и сделать замену переменной.
можно в знаменателе подынтегральной функции выделить полный квадрат и сделать замену переменной.
Например, для  преобразуем знаменатель подынтегральной функции
преобразуем знаменатель подынтегральной функции  . Сделаем замену переменной t = x- 2. Тогда х = t+ 2, dx = dt.
. Сделаем замену переменной t = x- 2. Тогда х = t+ 2, dx = dt.
 .
.
Получили сумму из двух интегралов. Второй интеграл табличный  , где а = 1, а в первом интеграле сделаем замену переменной u = t 2 – 1, тогда tdt = du/ 2.
, где а = 1, а в первом интеграле сделаем замену переменной u = t 2 – 1, тогда tdt = du/ 2.

d) Данный интеграл находится методом интегрирования по частям:
 .
.
Пусть  . Тогда по формуле интегрирования по частям:
. Тогда по формуле интегрирования по частям:


Задача 10
Найти определенные интегралы:
a)  ;
;
b)  ;
;
с) найти площадь фигуры ограниченной кривой  и осью абсцисс.
и осью абсцисс.
Решение:
a) Для вычисления интеграла используем метод непосредственного интегрирования. В результате получим:

b) Для вычисления данного интеграла воспользуемся методом замены переменной. Пусть t = sin (2 x), тогда dt = (sin 2 x) ´dx = 2 ·cos (2 x) dx. Следовательно cos (2 x) dx = dt/ 2. Также необходимо заменить пределы интегрирования, так как произошла замена исходной переменной:
 .
.

с) Площадь фигуры, ограниченной сверху кривой y = f(x), снизу осью OХ, слева прямой x = a и справа прямой y = b можно вычислить по формуле Ньютона–Лейбница:  , где F(x) – первообразная для функции f(x).
, где F(x) – первообразная для функции f(x).
Фигура ограничена сверху графиком кривой  , снизу осью ОХ. Эта площадь находится как интеграл от функции f(x), а пределы интегрирования – координаты точек пересечения параболы с осью OX. Найдем эти точки, решив уравнение
, снизу осью ОХ. Эта площадь находится как интеграл от функции f(x), а пределы интегрирования – координаты точек пересечения параболы с осью OX. Найдем эти точки, решив уравнение  . Корнями данного уравнения являются числа:
. Корнями данного уравнения являются числа:  и
и  . Поэтому нижний предел интегрирования равен 0, а верхний равен 2. Тогда:
. Поэтому нижний предел интегрирования равен 0, а верхний равен 2. Тогда:

Задача 11
Найти первые частные производные функций.
a)  ;
;
b)  .
.
Решение:
Частные производные функции двух и более переменных определяется по тем же формулам и правилам, что и функция от одной переменной. Следует помнить одно правило: если по одной переменной дифференцируем функцию, то остальные переменные считаются постоянными в этой функции.
a) Имеем функцию от двух переменных х и у:  . Тогда частные производные:
. Тогда частные производные:
 ,
, 
b) Данная функция является функцией от трех переменных x, y, z:  . Тогда частные производные:
. Тогда частные производные:
 ;
;
 ;
;
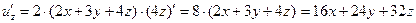 .
.
Задача 12
Найти градиент функции z (x;y) в точке (хо, уо), если z= cos (2 x + 11 y), x0 = y0 = π/ 2
Решение:
Градиентом функции z (x;y) называется вектор с координатами (z´x, z´y).
Имеем:  ,
, 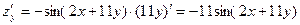 . Найдем значения частных производных в точке x0 = y0 = π /2:
. Найдем значения частных производных в точке x0 = y0 = π /2:


Градиент функции z в точке (π /2; π /2): 
Задача 13
Исследовать на экстремум функцию z = х 2 - ху + (у + 1)2.
Решение:
Найдем первые частные производные функции: 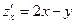 ;
;  . Точки, в которых частные производные не существуют, отсутствуют. Найдем критическую точку, решая систему уравнений:
. Точки, в которых частные производные не существуют, отсутствуют. Найдем критическую точку, решая систему уравнений:  . Отсюда получаем точку М (-2/3; -4/3). Найдем частные производные второго порядка данной функции:
. Отсюда получаем точку М (-2/3; -4/3). Найдем частные производные второго порядка данной функции:  ,
,  ,
,  . Найдем значение
. Найдем значение  > 0, при этом
> 0, при этом  > 0. Следовательно функция имеет минимум в точке М (-2/3; -4/3).
> 0. Следовательно функция имеет минимум в точке М (-2/3; -4/3).
Задача 14
Найти общее решение дифференциальных уравнений и проверить правильность найденных решений дифференцированием:
a)  ;
;
b)  .
.
Решение:
Данное дифференциальное уравнение относится к виду  , допускающему понижение порядка до тех пор, пока не получим решение уравнения. Для этого необходимо проинтегрировать правую и левую часть уравнения. Полученное уравнение имеет порядок на единицу ниже, чем исходное, то есть:
, допускающему понижение порядка до тех пор, пока не получим решение уравнения. Для этого необходимо проинтегрировать правую и левую часть уравнения. Полученное уравнение имеет порядок на единицу ниже, чем исходное, то есть:  .
.
a) Решим дифференциальное уравнение первого порядка  . Получим:
. Получим:
 .
.
Для того чтобы проверить правильность найденного решения, необходимо найти производную найденной функции:  . Получим исходное дифференциальное уравнение. Следовательно найденное решение верно.
. Получим исходное дифференциальное уравнение. Следовательно найденное решение верно.
b) Решим дифференциальное уравнение второго порядка с помощью двукратного интегрирования  . Тогда:
. Тогда:  ,
,  .
.
Проверим правильность найденного решения. Для этого найдем первую и вторую производную найденной функции.  ,
,  .
.
Получим исходное дифференциальное уравнение. Следовательно найденное решение верно.
Задача 15
Найти решения дифференциальных уравнений с разделяющимися переменными:
a) 
b) 
Решение:
Уравнения вида:  называется дифференциальным уравнением первого порядка с разделяющими переменными. В нем одно слагаемое зависит только от х, а другое – от у. Проинтегрировав почленно это уравнение, получаем:
называется дифференциальным уравнением первого порядка с разделяющими переменными. В нем одно слагаемое зависит только от х, а другое – от у. Проинтегрировав почленно это уравнение, получаем: 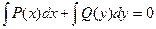 - это общий интеграл.
- это общий интеграл.
a) Разделим обе части уравнения  на
на  :
:  . Проинтегрируем обе части уравнения и получим:
. Проинтегрируем обе части уравнения и получим:  (произвольную постоянную здесь удобно записать именно так), где С > 0. Тогда
(произвольную постоянную здесь удобно записать именно так), где С > 0. Тогда  - общий интеграл исходного уравнения. При делении на
- общий интеграл исходного уравнения. При делении на  мы могли потерять решение y = -1 и x = 1. Так как С > 0, то оно не содержится в общем интеграле. Таким образом данное уравнение имеет особые решения: y = -1 и x = 1.
мы могли потерять решение y = -1 и x = 1. Так как С > 0, то оно не содержится в общем интеграле. Таким образом данное уравнение имеет особые решения: y = -1 и x = 1.
b) Уравнение вида  также сводится к уравнению с разделяющимися переменными.
также сводится к уравнению с разделяющимися переменными.
Решим уравнение:  . Поскольку
. Поскольку  , то
, то  . Разделим переменные:
. Разделим переменные:  . Проинтегрировав обе части уравнения получим:
. Проинтегрировав обе части уравнения получим:  . Выразим у:
. Выразим у:  . Это общее решение дифференциального уравнения.
. Это общее решение дифференциального уравнения.
При разделении переменных произошло деление на  , поэтому мы могли потерять решение y = 0. Оно не содержится в общем решении. Таким образом данное уравнение имеет особое решение y = 0.
, поэтому мы могли потерять решение y = 0. Оно не содержится в общем решении. Таким образом данное уравнение имеет особое решение y = 0.
Задача 16
Найти решение линейного однородного уравнения с постоянными коэффициентами: у" -2 у' + 10 у = 0 с условиями у = 0, у' = 1 при х = 0.
Решение:
Уравнения вида  , где p и q постоянные, называется линейным однородным дифференциальным уравнением с постоянными коэффициентами. Для решения необходимо составить характеристическое уравнение
, где p и q постоянные, называется линейным однородным дифференциальным уравнением с постоянными коэффициентами. Для решения необходимо составить характеристическое уравнение 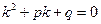 , заменив
, заменив  на
на  соответственно. При решении характеристического уравнения возможны следующие три случая:
соответственно. При решении характеристического уравнения возможны следующие три случая:
1. корни уравнения k1 , k2 - действительные и различные, тогда общее решение дифференциального уравнения имеет вид: 
2. корни уравнения k1 , k2 - действительные и равные, тогда общее решение дифференциального уравнения имеет вид: 
3. корни уравнения k1 , k2 - комплексно-сопряженные, то есть  , тогда общее решение дифференциального уравнения имеет вид:
, тогда общее решение дифференциального уравнения имеет вид: 
Решим уравнение 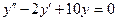 . Составим характеристическое уравнение:
. Составим характеристическое уравнение:  . Корни уравнения
. Корни уравнения  . В этом случае общее решение уравнения имеет вид:
. В этом случае общее решение уравнения имеет вид:  .
.
 .
.
Подставляя начальные условия у = 0, у' = 1 при х = 0 в полученное общее решение и его производную, получаем систему уравнений относительно С1 и С2 :


Найденные константы подставляем в общее решение. Получаем искомое частное решение уравнения, удовлетворяющее начальным условиям: 
Задача 17
Найти решение линейного неоднородного уравнения с постоянными коэффициентами в виде суммы общего решения однородного уравнения и произвольного частного решения неоднородного уравнения:
у" - 2  у' + у = 5.
у' + у = 5.
Решение:
Общее решение данного уравнения представим в виде:  , где
, где  - общее решение однородного уравнения, а
- общее решение однородного уравнения, а  - частное решение неоднородного уравнения.
- частное решение неоднородного уравнения.
Найдем общее решение однородного уравнения  . При решении характеристического уравнения
. При решении характеристического уравнения  получим корни
получим корни  . Тогда
. Тогда 
Частное решение для линейного уравнения, в правой части которого стоит константа, ищется в виде  , где А – константа. Подставив это решение в исходное уравнение и учитывая что производная от константы равна нулю, получим А = 5, следовательно
, где А – константа. Подставив это решение в исходное уравнение и учитывая что производная от константы равна нулю, получим А = 5, следовательно  .
.
Общее решение неоднородного уравнения  .
.






