Медианой вариационного ряда называется значение признака генеральной совокупности, приходящееся на середину вариационного ряда. В данном случае это варианта, расположенная в середине вариационного ряда. В середине данного ряда располагается варианта 15.
___________________________________________________________
Дан доверительный интервал 
для оценки математического ожидания нормально распределенного количественного признака. Тогда при увеличении надежности (доверительной вероятности) оценки доверительный интервал может принять вид … ☻(24,04; 28,38)
Доверительный интервал для оценки математического ожидания нормально распределенного количественного признака можно представить в виде симметричного интервала 
, где точечная оценка математического ожидания 
, а точность оценки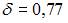 
. В случае увеличения надежности точность оценки ухудшается, то есть значение 
будет больше 0,77.
____________________________________________________
Выборочное уравнение прямой линии регрессии 
на 
имеет вид 
. Тогда выборочный коэффициент регрессии равен …☻ -1,5
Если выборочное уравнение парной регрессии имеет вид 
, то выборочный коэффициент регрессии равен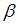 
. То есть 
.
По выборке объема 
найдена выборочная дисперсия 
. Тогда исправлен среднее квадрат откл равно …☻2,0
Дан доверительный интервал для оценки математического ожидания нормально распределенного количественного признака. Тогда при увеличении надежности (доверительной вероятности) оценки доверительный интервал может принять вид …☻(24,04; 28,38)
Проведено пять измерений (без систематических ошибок) некоторой случайной величины (в мм): 4,5; 5,2; 6,1; 7,8, 8,3. Тогда несмещенная оценка математического ожидания равна ☻6,38
Несмещенная оценка математического ожидания вычисляется по формуле 
. То есть 
.
Медиана вариационного ряда 11, 13, 13, 14, 15, 
, 18, 19, 21, 24, 25, 25 равна 17. Тогда значение варианты равно …☻16
Медианой вариационного ряда называется значение признака генеральной совокупности, приходящееся на середину вариационного ряда. Так как в середине ряда располагаются две варианты: и 18, то медиана равна их средней арифметической, то есть 
. Тогда 
.
____________________________________________________________
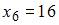Выборочное уравнение прямой линии регрессии на имеет вид 
. Тогда выборочный коэффициент корреляции может быть равен …☻- 0,67
Размах варьирования вариационного ряда 2, 3, 4, 5, 5, 7, 9, 10, 12, 14, 
равен 15. Тогда значение равно … 17
Дан доверительный интервал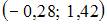 
для оценки математического ожидания нормально распределенного количественного признака. Тогда при уменьшении надежности (доверительной вероятности) оценки доверительный интервал может принять вид … (-0,14; 1,28)
Решение
Доверительный интервал для оценки математического ожидания нормально распределенного количественного признака можно представить в виде симметричного интервала , где точечная оценка математического ожидания 
, а точность оценки 
. В случае уменьшения надежности точность оценки улучшается, то есть значение будет меньше 0,85.
Из генеральной совокупности извлечена выборка объема 
:
Тогда выборочное среднее квадратическое отклонение равно …
| █ | 
| ||
Решение:
Выборочное среднее квадратическое отклонение вычисляется как 
, где
. Тогда
,
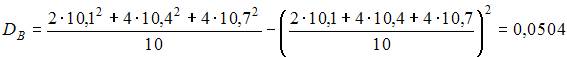и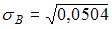 
Выборочное уравнение прямой линии регрессии на имеет вид . Тогда выборочный коэффициент корреляции может быть равен …
| █ | – 0,67 | ||
Решение
Значение выборочного коэффициента корреляции, во-первых, принадлежит промежутку 
, а во-вторых, его знак совпадает со знаком выборочного коэффициента регрессии. Этим условиям удовлетворяет значение 
.
