Функция
| С |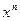 
| 
| 
| 
| 
| 
| 
| 
| 
|
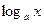
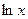
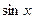
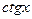
Производная
| 
|
| 
| 
|
| -
| 
| 
| 
|
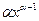
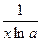
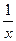
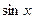
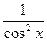
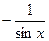
Уравнение касательной к графику функции в его точке с абсциссой 
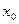имеет вид:
.
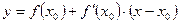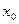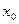Геометрический смысл производной: значение производной функции в его точке равно угловому коэффициенту касательной к графику функции , проведенной в точке , т.е.
.
Физический смысл производной: мгновенная скорость тела в момент времени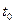 
, т.е.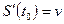 
(где S – перемещение). Ускорение тела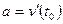 
или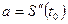 
(вторая производная перемещения по времени).
При исследовании функций производнаяиспользуется для нахождения:
- промежутков монотонности;
- экстремумов функции;
- наибольшего и наименьшего значений функции на отрезке.
Пример 1. Найдите значение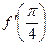 
, если 
.
Решение:
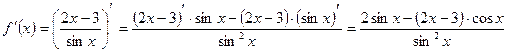
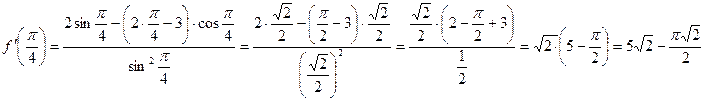
Ответ: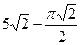 
.
Пример 2. Решить неравенство: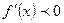 
, если 
.
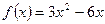Решение:
,
_
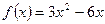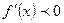
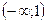
Ответ: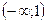
Лабораторные работы/Практические занятия
Не предусмотрены
Задания для самостоятельного выполнения:
- Найдите значение 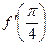, если
.
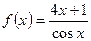Ответ: 
.
- Найдите значение
, если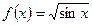 
.
Ответ: 
.
3. Решить неравенство: 
, если 
.
Раздел 2 «Комбинаторика»
Основные понятия и термины по разделу: перестановка, размещение, сочетание, правило суммы, правило произведения.
План изучения разделов (перечень вопросов, обязательных к изучению):
1. определение перестановки;
2. определение размещения;
3. определение сочетания;
4. правило суммы;
5. правило произведения.
Краткое изложение теоретических вопросов:
Все мы задавались когда- нибудь вопросом: сколькими способами можно что- то сделать? Ответ на этот вопрос дает наука комбинаторика.
Перестановками называют комбинации, состоящие из одних тех же n различных элементов и отличающиеся только порядком их расположения.
Число всех возможных перестановок находится по формуле: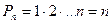 
!
Размещениями называют комбинации, составленные из различных элементов n по m элементов, которые отличаются либо составом элементов, либо их порядком.
Число всех возможных размещений вычисляется по формуле:
Сочетаниями называют комбинации, составленные из различных элементов n по m элементов, которые отличаются хотя бы одним элементом.
Число всех возможных сочетаний находится по формуле:
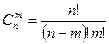
При решении задач комбинаторики используют правила суммы и произведения.
Правило суммы. Если некоторый объект A может быть выбран из совокупности объектов m способами, а другой объект B может бытьn способами, то выбрать либо A, либо B можно m+n способами.
Правило произведения. Если некоторый объект A может быть выбран из совокупности объектов m способами и после каждого такого выбора другой объект B может быть выбран способами n, то пара объектов 
в указанном порядке может быть выбрана 
способами.
Пример 1. В группе 34 учащихся. К доске нужно вызвать двоих. Сколькими способами это можно сделать, если: а) первый учащийся должен решить задачу по алгебре, а второй – по геометрии; б) они должны быстро стереть с доски?
Решение:
В случае а) порядок важен, а в случае б) – нет.
Значит под а)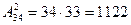 
; б) 
Лабораторные работы/Практические занятия
Не предусмотрены
Задания для самостоятельного выполнения:
Пример 1. В группе 34 учащихся, из них нужно выбрать троих. Сколькими способами это можно сделать, если: а) первый учащийся должен решить задачу, второй – сходить за мелом, третий – пойти дежурить в столовую; б) им следует спеть хором?
Ответ: а) 33728; б) 5984.
ПРИЛОЖЕНИЕ.
Площадь треугольника.
Обозначения:
Признаки подобия треугольников.
1)Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугоники подобны.
2)Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами равны, то такие треугольники подобны.
3)Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
Площади поверхностей и объемы тел вращения.
|
pr2 h
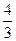pR3
