Основные понятия и термины по теме: определение логарифма, основные свойства логарифмов, свойства степени с действительным показателем.
План изучения темы (перечень вопросов, обязательных к изучению):
1. Свойства степеней с действительным показателем.
2. Определение логарифма.
3. Свойства логарифмов.
4. Десятичные и натуральные логарифмы.
Краткое изложение теоретических вопросов:
Основные свойства степеней приведены в теме 1.1
2. Логарифмом числа 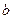 по основанию
по основанию 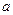 называют показатель степени, в которую нужно возвестио снование
называют показатель степени, в которую нужно возвестио снование 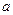 , чтобы получить число
, чтобы получить число 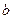 .
.
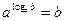 - основное логарифмическое тождество, где
- основное логарифмическое тождество, где 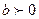 ,
, 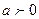 ,
, 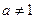
Основные свойства логарифмов.
При любом 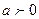 ,
, 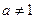 и
и 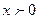 ,
, 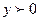
1) 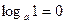 ; 2)
; 2) 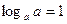 ; 3)
; 3) 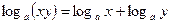 ;
;
4) 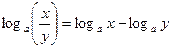 ; 5)
; 5) 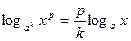 ;
;
6) 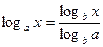 - формула перехода к другому основанию
- формула перехода к другому основанию
4. Логарифмы по основанию 10 называют десятичными и обозначают lg.
Натуральным логарифмом (обозначается ln) называется логарифм по основанию е:
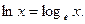
Пример 1. Вычислить: а) 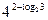 ; б)
; б) 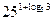 ; в)
; в) 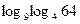 ;
; 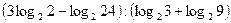 .
.
Решение:
а) 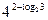 =
= 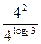 =
= 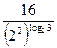 =
= 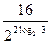 =
= 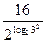 =
= 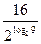 =
= 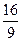 =
= 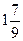
Ответ: 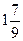 .
.
б) 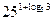 =
= 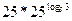 =
= 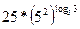 =
= 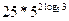 =
= 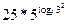 =
= 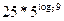 =
= 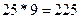
Ответ: 225.
в)) 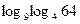 =
= 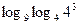 =
= 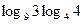 =
= 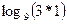 =
= 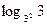 =
= 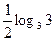 =
= 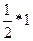 =
= 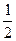 =0,5
=0,5
Ответ: 0,5.
г) 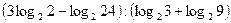 =
= 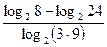 =
= 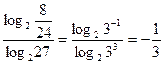 .
.
Лабораторные работы/Практические занятия
Не предусмотрены
Задания для самостоятельного выполнения:
1. Вычислите 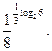
Ответ: 6.
2. Вычислите: 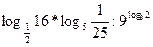 .
.
Ответ: 2.
3. Вычислите: 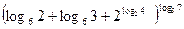
Ответ:7.
4. Найдите 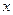 :
:
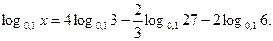
Ответ: 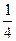 .
.
Тема 1.4 Функции.
Основные понятия и термины по теме: определение функции, нули функции, промежутки знакопостоянства, монотонность, четность, нечетность, линейная, квадратичная, показательная и логарифмическая функции.
План изучения темы (перечень вопросов, обязательных к изучению):
1. Определение функции
2. Нули функции
3. Определение возрастающей функции
4. Определение убывающей функции
5. Определение четной функции
6. Определение нечетной функции
7. Основные виды функций
1. Функцией с областью определения D называется соответствие, при котором каждому числу х из множества D сопоставляется по некоторому правилу (закону)число у из множества Е, зависящее от х. Такое правило (закон) является функцией y=f(x) c областью определения D и областью значений Е.

При этом величину х называют независимой переменной (или аргументом функции), величину у - зависимой переменной (или значением функции).
2. Точка пересечения графика функции с осью ординат равна значению функции 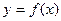 при х=0, т.е.
при х=0, т.е. 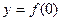 Точки пересечения графика функции с осью абсцисс(их еще называют нулями функции) являются корнями уравнения
Точки пересечения графика функции с осью абсцисс(их еще называют нулями функции) являются корнями уравнения 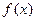 =0.
=0.
3. Промежутки знакопостоянства функции – те значения переменной х, при которых функция принимает положительные (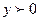 ) и отрицательные (
) и отрицательные (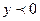 ) значения.
) значения.
4. Монотонность – возрастание или убывание функции. Функция y=f(x) называется возрастающей, если большему значению аргумента соответствует большее значение функции (т.е. если 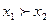 , то
, то 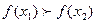 . Функция называется убывающей, если большему значению аргумента соответствует меньшее значение функции (т. е. если
. Функция называется убывающей, если большему значению аргумента соответствует меньшее значение функции (т. е. если 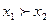 , то
, то 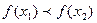 .
.
5. Функция называется четной, если при изменении знака аргумента значение функции не меняется, т.е. если для любого 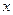 из ее области определения
из ее области определения 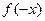 =
= 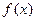 .
.
График четной функции симметричен относительно ординат.
6. Функция называется нечетной, если при изменении знака аргумента значение функции также меняется на противоположное, т.е. если для любого 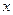 из ее области определения
из ее области определения 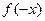 =-
=- 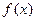 .
.
График нечетной функции симметричен относительно начала координат.
7.1. Функция заданная формулой 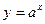 (где
(где 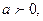
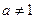 ), называется показательной функцией с основанием
), называется показательной функцией с основанием 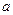 .
.
Свойства показательной функции:
1) Область определения – множество R действительных чисел.
2) Область определения – множество R+ всех положительных чисел.
3) При 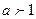 функция возрастает на всей числовой прямой; при
функция возрастает на всей числовой прямой; при 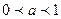
функция убывает на множестве R.
4) Основные свойства степеней приведены в теме 1.1
7.2.Функцию заданную формулой 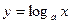 , называют логарифмической функцией с основанием
, называют логарифмической функцией с основанием 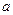 .
.
Свойства логарифмической функции:
1) Область определения – множество всех положительных чисел R+,
т.е D (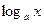 )= R+.
)= R+.
2) Область значений - множество всехдействительных чисел,
т.е. E (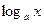 )= R.
)= R.
3) При 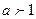 функция возрастает на всей области определения; при
функция возрастает на всей области определения; при 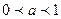
убывает.
Пример 1. Найти область определения функции у= log2 (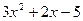 ).
).
Решение:
Область определения логарифмической функции – множество всех положительных чисел R+.
Поэтому заданная функция определена только для тех 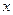 , при которых
, при которых 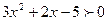 .
.
y= 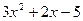
Графиком функции является парабола, ветви которой направлены вверх, так как а=3, 3 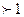 .
.
Найдем нули функции:
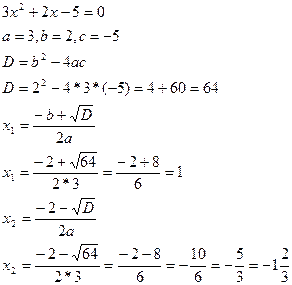
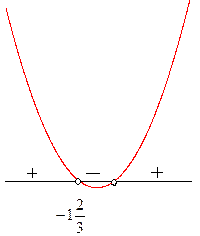 |
D(f)= 
Ответ: 
Пример 2. Найдите область определения функции: 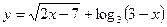
Решение:
По определению арифметического квадратного корня, подкоренное выражение должно быть не меньше нуля. Областью определения логарифмической функции является множество всех положительных чисел. Таким образом, составим систему неравенств:
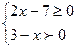 ;
; 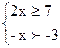 ;
; 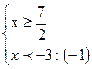 ;
; 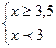 ; значит
; значит 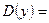
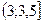
Ответ: 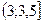
Пример 3. Найдите область определения функции 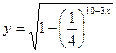
Решение:
По определению арифметического квадратного корня имеем:
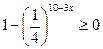
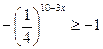
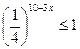
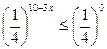
Т.к. 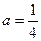 ,
, 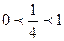 , то функция
, то функция 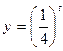 непрерывна и монотонно убывает на множестве R. Тогда
непрерывна и монотонно убывает на множестве R. Тогда 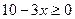
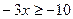
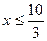
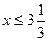 , значит
, значит 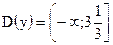
Ответ: 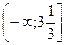
Пример 4. Найдите область определения функции 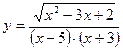
Решение:
Область определения задается системой неравенств:
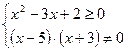 ;
;
1) 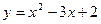
Графиком функции является парабола, ветви которой направлены вверх.
Найдем нули функции:
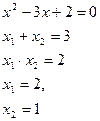
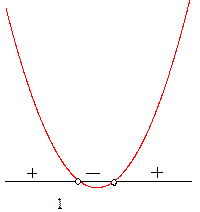 |
2) 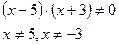
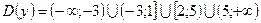
Ответ: 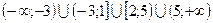 .
.
Лабораторные работы/Практические занятия
Не предусмотрены
Задания для самостоятельного выполнения:
1. Найдите область определения функции:
а) 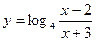
Ответ: 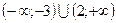 .
.
б) 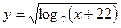
Ответ: 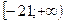
в) 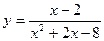
Ответ:  .
.






