Автоматизи́рованное рабо́чее ме́сто (АРМ) — программно-технический комплекс, предназначенный для автоматизации деятельности определенного вида. При разработке АРМ для управления технологическим оборудованием как правило используют SCADA-системы.
АРМ объединяет программно-аппаратные средства, обеспечивающие взаимодействие человека с компьютером, предоставляет возможность ввода информации (через клавиатуру, компьютерную мышь, сканер и пр.) и её вывод на экран монитора, принтер, графопостроитель, звуковую карту — динамики или иные устройства вывода. Как правило, АРМ является частью АСУ.
Базой новых информационных технологий в области ветеринарии являются персональные компьютеры. Стационарные компьютеры устанавливают в административных зданиях хозяйств и предприятий, на их базе создают автоматизированные рабочие места (АРМ) ветеринарных врачей на фермах, в цехах. С помощью портативных компьютеров автоматизируются информационные процессы при обслуживании отдельных производственных участков, кооперативов и фермерских хозяйств. Функциональное назначение программного комплекса — автоматизация процессов учета, планирования, диагностики, лечения, профилактики, экономики и отчетности
30. Основные понятия теории вероятностей. Пространство элементарных исходов и случайные события
Теория вероятностей – математическая наука, изучающая закономерности в случайных явлениях. Одним из основных понятий теории вероятностей является понятие случайного события (или просто события).
Событием называется любой факт, который в результате опыта может произойти или не произойти. Примеры случайных событий: выпадение шестерки при подбрасывании игральной кости, отказ технического устройства, искажение сообщения при передаче его по каналу связи. С событиями связываются некоторые числа, характеризующие степень объективной возможности появления этих событий, называемые вероятностями событий.
Современное построение теории вероятностей основывается на аксиоматическом подходе и опирается на элементарные понятия теории множеств. Такой подход называется теоретико-множественным.
Достоверным называется событие W, которое происходит в каждом опыте.
Невозможным называется событие Æ, которое в результате опыта произойти не может.
Несовместными называются события, которые в одном опыте не могут произойти одновременно.
Суммой (объединением) двух событий A и B (обозначается A + B, A È B) называется такое событие, которое заключается в том, что происходит хотя бы одно из событий, т.е. A или B, или оба одновременно.
Произведением (пересечением) двух событий A и B (обозначается A × B, A Ç B) называется такое событие, которое заключается в том, что происходят оба события A и B вместе.
Противоположным к событию A называется такое событие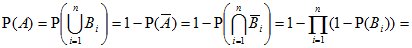 
, которое заключается в том, что событие A не происходит.
События Ak (k =1, 2,..., n) образуют полную группу, если они попарно несов Случайные события и их классификация, операции над событиями.
Событием называется любой факт, который в результате опыта может произойти или не произойти. Примеры случайных событий: выпадение шестерки при подбрасывании игральной кости, отказ технического устройства, искажение сообщения при передаче его по каналу связи. С событиями связываются некоторые числа, характеризующие степень объективной возможности появления этих событий, называемые вероятностями событий.
При преобразовании выражений можно пользоваться следующими тождествами:
.
На основе вышеизложенного сформулированы аксиомы теории вероятностей. Пусть каждому событию ставится в соответствие число, называемое вероятностью события. Вероятность события A обозначается P(A). Так как событие есть множество, то вероятность события есть функция множества. Вероятности событий удовлетворяют следующим аксиомам.
1. Вероятность любого события заключена между нулем и единицей:
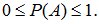(1.1)
2. Если A и B несовместные события, то
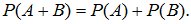(1.2)
Вторая аксиома обобщается на любое число событий: 
если события Аi и Aj попарно несовместны для всех i≠j
События A1, A2, …, An называют равновозможными если
P(A1)=P(A2)= … =P(An). (1.3)
Если в каком-то опыте пространство элементарных событий Ω можно представить в виде полной группы несовместных и равновозможных событий ω1, ω2, …, ωn, то такие события называются случаями, а сам опыт сводится к схеме случаев.
Случай ωi называется благоприятным событием A, если он является элементом множества A: 
.
Классическое определение вероятност и: вероятность события определяется по формуле
, (1.4)
где n - число элементарных равновозможных исходов данного опыта;
m - число равновозможных исходов, приводящих к появлению события.
31. Распределение хи-квадрат.
Распределение хи-квадрат применяется для проверки статистических гипотез.
где m-эмпирические частоты
m1- теоретические частоты
n- число степеней свободы
При полном совпадении эмпирических частот с частотами вычисленными или ожидаемыми хи-квадрат равен 0 если же не равно 0 это укажет на несоответствие вычисленных частот эмпирическим частотам ряда. В таких случаях необходимо оценить значимость критерия хи-квадрат которое теоритически может изменяться от 0 до ∞ это производится путем сравнения его фактически полученного значения с его критическим значением. Гипотеза отвергается если хи-квадрат ≥ критического значения для принятого уровня значимости и числа степеней свобод.
Для определения критерия хи-квадрат необходимо найти теоретические частоты-равновероятные частоты- сложение всех частот и деление на количество категорий.
Для определения стандартного значения хи-квадрат число степеней свободы
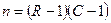где R – количество строк в таблице
С количество столбцов
32. Распределение Стьюдента.
Представляет собой сумму нескольких нормальных распределений случайных величин. Высчитывается по формуле для нахождения критерий. Полученные значения сравнивают до стандартного значения таблицы Стьюдента с учётом вероятности и числа степеней свободы.
33. Распределение Фишера.
Данное распределение нашло применение при построение интервальных оценок и статистических критериев, отношение двух выборочных дисперсий вычисленных по двум выборкам извлеченных из одной генеральной совокупности. Если имеются 2 случайных величины X и Y подчиняющихся закону распределения хи-квадрат со степенями свободы a и b соответственно то отношение 
- распределение Фишера, f- распределение с числом степеней свободы a и b.
34. Коэффициент корреляции.
Коэффициент корреляции показывает степень статистической зависимости между двумя числовыми переменными. Коэффициент корреляции варьирует от -1 до 1. При отрицательном показателе: при увеличение одного признака показатель другого признака снижается. При положительном: при повышении одного признака повышается и другой.
35. Двумерное нормальное распределение.
2 переменные имеют двумерное нормальное распределение если для каждого фиксированного значения одной переменной имеется соответствующее значение другой переменной. Свойственно для биологических признаков.
36. Статистические данные. Понятие генеральной совокупности и случайной выборки.
Статистические данные — это совокупность объектов (наблюдений, случаев) и признаков (переменных), их характеризующих. Генеральная совокупность- большое количество исследуемых наблюдений. Выборка- случайная совокупность испытуемых из общего числа, тех на которых можно будет распространять полученные в результате изучения совокупности.
37. Переменные и наблюдения, количественные, номинальные и ранговые переменные.
Переменные- характеристики изучаемых объектов. Наблюдения- числовые или номинальные данные переменных.
Номинальные переменные- нечисловые, означают принадлежность к классам, не могут быть использованы при вычислениях или упорядочены.
Количественные- выражены в единицах измерения; например, вес, рост, кровяное давление, число приступов астмы в определенный период и т.п.
Ранговые- данные упорядочены но не могут быть с уверенностью измерены и сопоставлены. К таким переменным применимы ранговые методы.
38. Статистическое оценивание. Понятие статистической оценки.
