Измерение и кодирование информации

Количество информации

Как отмечалось в Главе 1, разработаны подходы к определению понятия "количество информации". Эти подходы, основаны на том, что явление информации представляет собой совокупность объектов, которые могут обладать некоторым набором состояний и мы получаем некоторое сообщение о состоянии этих объектов. Пусть у нас имеются некоторые знания об объектах до появления и после появления сообщения. Эти знания можно количественно описать (говорят информацию, «содержащуюся» в сообщении можно количественно описать-измерить). Для этого количественно фиксируется уменьшение неопределённости наших знаний об объекте при получении сообщения. Более конкретно - используют математические понятия вероятности состояния объекта (до получения сообщения и после получения сообщения) и понятие логарифма этих вероятностей.

Рассмотрим эти понятия более подробно.

Для введения количественной меры синтаксической информации, которая получила название количество информации по Шеннону - I, потребуется рассмотреть вероятностную математическую модель данных или сообщений. Кроме того, количество информации I на синтаксическом уровне невозможно определить без рассмотрения понятия неопределённости состояния системы (энтропии системы). Рассмотрим это понятие подробнее. Для этого введем понятие источника сообщений.

Пусть источник сообщений есть явление, которое порождает последовательность символов X_k,i длиной n (i=1,n). Сообщением можно считать каждый символ в этой последовательности. Иногда удобнее под сообщением понимать фрагмент этой последовательности. В этом случае отдельный символ в этом фрагменте будет называться элементом сообщения.

Согласно математической модели сообщения каждый символ типа k появляется случайно из алфавита объемом m. Фактически речь идет о появлении символа, как случайном событии. Вероятность появления этого символа равна: 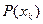. Мера неопределенности появления именно данного символа количественно описывается математической величиной получившей название удельная энтропия на один элемент сообщения:

Можно считать эту неопределенность сообщения априорной (до опыта). Однако если получено (это и есть опыт) другое случайное событие (сообщение) содержащее некий символ Y_r,i, которое статистически связано с появлением символа X_k,i то возможно вычисление апостериорной энтропии (после опыта): .

Здесь – вероятность появления символа X_k,i; 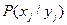это условная вероятность появления символа X_k,i при условии что символ Y_r,i уже появился.

Теперь можно определить количество информации по Шеннону как уменьшение степени неопределенности появления конкретного символа X_k,i сообщения, после того как появился символ Y_r,i в виде разности априорной и апостериорной энтропий.

I = H(x) - H (x/y)

Можно дать несколько более обобщенную формулировку с учетом выше изложенного, если под источником сообщений понимать явление (систему) любой природы a (конечный автомат) состояния которой трактуются как символы определенного типа. Тогда априорная энтропия системы H(a), имеющая N возможных состояний равна:

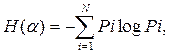
где Pi – вероятность того, что система находится в i -м состоянии.

После того как появилось некоторое явление b, связанное с системой причинно-следственными связями (сообщение b) неопределенность (апостериорная энтропия системы) H(a/b), уменьшилась. Тогда количество информации I(a) о системе, полученной в сообщении b, определяется как

I (a) = H(a) – H(a/b),

т.е. количество информации измеряется (уменьшением) неопределённости состояния системы.

Если апостериорная неопределённость H(a/b), обратится в нуль, то первоначальная апостериорная, неопределенность заменится полной определенностью и количество информации I (a) = H(a). Это частная ситуация в литературе трактуется как негэнтропия Бриллюэна.

Для случая, когда все состояния системы равновероятны, т. е. их вероятности равны, а число состояний равно N имеем:

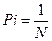, где энтропия системы определяется соотношением

Если источник сообщения имеет алфавит размером m, а число возможных символов в сообщении равно n, то число возможных оригинальных сообщений будет равно: M=mⁿ .

Примером сообщения является текст. Любой текст состоит из конечного числа символов (букв). Полный набор букв называется алфавитом. Напомним, что от символов букв легко прейти к числам. Этот процесс и называется кодированием. При кодировании происходит преобразование букв в соответствующие числа (кодовые символы). Сами числа могут задаваться в разных системах счисления. Естественно, что одно и то же количество разрядов в разных системах счисления может передать разное число состояний отображаемого объекта, что можно представить в виде соотношения

M=mⁿ ,

где M – число всевозможных отображаемых состояний;

m – основание системы счисления (разнообразие символов, применяемых в алфавите),

n – число разрядов (символов) в сообщении.

Если m =2 то это двоичная система счисления. Именно эта система счисления и является основной для архитектуры ЭВМ. Поэтому в современных ЭВМ минимальной единицей измерения данных является бит - один двоичный разряд. Широко используются также более крупные единицы измерения: байт, равный 8 битам; килобайт, равный 1024 байтам; мегабайт, равный 1024 килобайтам и т.д.

При этом «получение информации» рассматривается как получение одного сообщения из конечного наперёд заданного множества из N равновероятных сообщений, то есть оно расценивается как вероятностное событие. Тогда количество информации Q, содержащееся в выбранном сообщении, определяется как двоичный логарифм N (формула Хартли) Q = log₂N.

Содержательный подход связывает количество информации с содержанием сообщения. Так, при броске монеты на ровную поверхность она ложится стороной "орел" или "решка". До броска монеты неопределенность количественно выражалась в двух равновероятных событиях, после броска имеет место одно событие – "орел" или "решка", следовательно неопределенность знания уменьшилась в два раза.

Для двух равновероятных сообщений ("орел" и "решка") по формуле Хартли получим Q = log₂2 = 1.

В качестве единицы информации принят один бит (англ. bit — binary digit — двоичная цифра). Итак, бит в теории информации – это такое количество информации, которое содержит сообщение, уменьшающее неопределенность знания в два раза.

Допустим, на игральном кубике на каждой грани нанесены от 1 до 6 точек, причем выигрышными являются значения граней от 4 до 6. Вероятность того, что одна из граней будет верхней после броска равна 1/6. Обозначая вероятные события как "проигрыш" и "выигрыш", получим вероятность проигрыша, равную 1/6 + 1/6 + 1/6 = 1/2 и такую же вероятность выигрыша. То есть, как и при броске монеты, каждый бросок кубика в данной игре будет содержать сообщение с количеством информации в один бит.

Вероятностный подход позволяет оценить количество получаемой информации для событий, которые происходят с разной вероятностью. Рассмотрим пример, когда вероятности событий отличаются. Пусть в урне находятся 4 белых и 12 черных шаров. Вероятность вытащить наудачу белый шар равна 4/(4+12) = 1/4, а черный 12/(4+12) = 3/4.

Качественную связь между вероятностью события и количеством информации в сообщении об этом событии можно выразить так: чем меньше вероятность некоторого события, тем больше информации содержит сообщение об этом событии.
Количественная зависимость между вероятностью события р и количеством информации в сообщении о нем I выражается формулой I= -log₂p.

Так, при извлечении белого шара мы получаем количество информации I = -log₂(1/4) = 2 бит, а при извлечении черного шара мы получаем количество информации I = -log₂(3/4) = 0,3 бит.

Напомним, что алфавитный подход (синтаксический подход) не связывает количество информации с содержанием (смыслом) сообщения.

Этот подход используется при последовательных операциях передачи, сохранения, чтения текста, в котором все множество используемых в языке типов символов традиционно называют алфавитом.

Исходным значением для количественной оценки передаваемой информации является полное число символов алфавита, которое принято называть мощностью (объемом) алфавита.

Допустим, алфавит текста включает прописные и строчные символы кириллицы, цифры, знаки препинания, символы арифметических операций и прочие вспомогательные символы, вся же мощность алфавита пусть будет равна 128.

Предположим также, что каждый очередной символ при последовательных операциях передачи, сохранения или чтения текста с одинаковой вероятностью может быть любым символом алфавита. (В действительности это не совсем так, но для упрощения примем такое предположение.)

В каждой очередной позиции текста может появиться любой из N символов. Каждый символ несет Q=I бит информации; число Q можно определить из уравнения Q = log₂N.

Для N = 128 получаем: Q= 7 бит.

Затем для того, чтобы найти количество информации во всем тексте, нужно посчитать число символов в нем и умножить на Q.

В вычислительной технике и теории цифровой связи битом называют значение двоичного разряда памяти компьютера, необходимого для хранения одного из двух знаков «0» и «1», используемых для внутримашинного представления данных и команд.

Пример 1. Если мы бросим монету на ровную поверхность, то с равной вероятностью произойдет одно из двух возможных событий – "орел" или "решка". Неопределенность, существовавшая до броска ("орел" или "решка") уменьшается в два раза. Поскольку количество информации, которое мы получаем после броска, равно 1 бит, то для сохранения результата броска понадобится один двоичный разряд, куда будет занесена 1, если результат броска "орел" или 0, если результат броска "решка" (либо наоборот 0 для "орел" и 1 для "решка").

Пример 2. Правильная четырехгранная пирамида имеет грани красного, желтого, зеленого и синего цвета. Если бросить такую пирамиду на ровную поверхность, то произойдет одно из 4-х возможных событий – пирамида ляжет на одну из цветных граней. Какое количество информации будет получено после броска пирамиды?

Для четырех равновероятных сообщений по формуле Хартли получим Q = log₂4 = 2 бит.

Таким образом, для сохранения результата броска понадобится два двоичных разряда (2 бита), куда будет занесены:

00 – если результат броска "красная" грань;

01 – если результат броска "желтая" грань;

10 – если результат броска "зеленая" грань;

11 – если результат броска "синяя" грань;

Двоичное число, соответствующее событию (сообщению), называют кодом этого события. Коды цветов назначены произвольно, так как это не имеет особого значения.

Пример 3. Допустим, количество различных символов, вводимых с клавиатуры в компьютер, равно 256. Какое количество информации передается в компьютер при нажатии одной из клавиш (комбинаций клавиш)?

 

Таблица 2.16

ASCII-коды некоторых символов для кодовой таблицы CP866

ASCII – код двоичный	ASCII – код десятичный	Символ
		А
		Б
		В
		Г
...	...	...
		э
		ю
		я
...	...	...

 

Для 256 равновероятных сообщений по формуле Хартли получим Q = log₂256 = 8 бит

Таким образом, нажатие клавиши (комбинаций клавиш) клавиатуры представляет собой передачу информации в компьютер размером 8 бит. Очевидно, что двоичный код каждого символа клавиатуры в данном случае является восьмиразрядным. Такой код используется в текстовом режиме (т.н. ASCII-режим). В табл. 2.16 даны ASCII-коды некоторых символов.