Кроме арифметических операций над знаками (символами) необходимо осуществлять логические операции. Далее более детально описываются эти логические операции и их физическое воплощение в виде устройств компьютера.
Как отмечалось в Главе 1логические системы, предназначены для описания и получения правильных суждений, представляющих собой совокупность связанных меду собой понятий. Различают простые суждения (простые логические высказывания) связывающие два понятия и сложные суждения (составные логические высказывания) связывающие несколько понятий. Часто вместо термина суждение используется термин логическое высказывание. На основе суждений можно строить специальные логические конструкции, получившие название логических выводов (фигура силлогизма, умозаключение). Элементарные объекты, участвующие в логических построениях – простые суждения (далее суждения или логические высказывания) это суждение в отношении которых можно фиксировать один из двух символов («0» или «1»). Можно вместо символов «0» или «1» использовать варианты последовательностей символов «ложь» или «истина». Другой вариант последовательность символов «да» или «нет». В более образной форме часто говорят, что простые суждения это такие суждения, истинность которых можно установить.
Математическая дисциплина, обеспечивающая строго математическое описание логических высказываний с использованием алгебраических обозначений и методов получила название математической логики. Элементы математической логики необходимые для изучения информатики и объяснения работы компьютера и компьютерных программ излагаются ниже.
Логическим высказыванием называется утверждение, в отношении которого всегда можно однозначно сказать, истинно оно или ложно (то есть принимает значение «истина» или «ложь»).
Например, утверждения «Рекс – собака», «6 – четное число» следует считать логическими высказываниями, так как они истинные. Утверждения «Слоны умеют летать» или «Рим – столица Франции» также являются высказываниями, так как они ложные.
Вопросительные и восклицательные предложения не могут быть логическими высказываниями, так как они ничего не утверждают, также не являются высказываниями предложения типа «Увлекательное занятие» или «Студент первого курса».
Предложения типа «В городе N более миллиона жителей» не является высказыванием, поскольку не известно, о каком именно городе идет речь. Здесь присутствует логический объект « N», который называется предметной переменной. Предложение станет логическим высказыванием только после конкретизации, то есть замены переменной «N» конкретным значением. Например, если N примет значение «Санкт-Петербург», то это утверждение станет истинным, то есть будет высказыванием.
Утверждение, прямо или косвенно содержащее хотя бы одну переменную, и истинность которого можно установить, когда все предметной переменные замещаются своими значениями, называется предикатом (высказывательной формой).
Другие примеры предикатов: «X – брат Y», «Число A больше 5».
Значения «истина» и «ложь» называются истинностными или логическими значениями. В разных системах они могут обозначаться по-разному, например:
| Истина | И | True | |
| Ложь | Л | False |
Сами высказывания принято обозначать буквами латинского алфавита, например, A, B, p, q.
Элементарные логические высказывания, обозначенные буквами, которые не зависят друг от друга и могут принимать значения «истина» или «ложь», называют пропозициональными переменными.
Связывая элементарные логические высказывания с помощью логических операций, можно получить составные высказывания.
Например, связывая два высказывания «Вчера было холодно» и «Вчера шел дождь» с помощью операции конъюнкция (логическое «И»), получаем новое высказывание «Вчера было холодно и шел дождь».
Каждая логическая операция производится над логическими значениями (которые в этом случае называются операндами) и имеет свое название и обозначение. Если операция производится над одной пропозициональными переменной, она называется унарной; операция над двумя логическими переменными называется бинарной.
Определим следующие логические операции: унарная операция отрицание, бинарные операции: конъюнкция, дизъюнкция и импликация, эквивалентность.
1. Отрицание, инверсия,логическое «НЕ».
Обозначается словом not, чертой над обозначением высказывания или знаком Ø, например, not A, 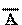 , ØA.
, ØA.
Высказывание ØA принимает значение «истина», если A ложно, и значение «ложь», когда A – «истина».
Пример: «Луна – спутник Земли» (А);
«Луна – не спутник Земли» (ØA).
Результат логической операции задается таблицей истинности – таблицей, в которой указываются все возможные сочетания значений операндов и соответствующее каждому сочетанию значение результата (табл.2.1).
Таблица 2.1
Таблица истинности операции логическое «НЕ»
| значение операнда A | значение ØA |
| истина | ложь |
| ложь | истина |
В таблице истинности могут стоять другие обозначения истинностных значений, например, не «истина» и «ложь», а 1 и 0 соответственно.
2. Конъюнкция, логическое «И», логическое умножение.
Обозначается словом and, знаками × (точка), Ù или &, например, A Ù B.
Высказывание A Ù B истинно тогда и только тогда, когда оба высказывания А и В истинны (табл. 2).
Можно также сказать, что A Ù B истинно, если истинно и А, и B одновременно.
Например, высказывание «10 делится на 2 и 5 больше 3» истинно, а высказывания «10 делится на 2 и 5 не больше 3»,«10 не делится на 2 и 5 больше 3», «10 не делится на 2 и 5 не больше 3» – ложны.
Таблица 2.2
Таблица истинности операции логическое «И»
| значение операнда A | значение операнда В | значение A Ù B |
| истина | Истина | истина |
| истина | Ложь | ложь |
| ложь | Истина | ложь |
| ложь | Ложь | ложь |
3. Дизъюнкция, логическое «ИЛИ», логическое сложение.
Обозначается словом or, знаками +, Ú, |, например, A Ú B.
Высказывание A Ú B ложно тогда и только тогда, когда оба высказывания А и В ложны.
Можно также сказать, что высказывание A Ú B истинно, если истинно хотя бы одно из высказываний A, B (табл. 3).
Другими словами, A Ú B истинно, если истинно или A, или B, или и A, и B одновременно.
Например, высказывание «10 не делится на 2 или 5 не больше 3»ложно, а высказывания «10 делится на 2 или 5 больше 3», «10 делится на 2 или 5 не больше 3», «10 не делится на 2 или 5 больше 3» – истинны.
Таблица 2.3
Таблица истинности операции логическое «ИЛИ»
| значение операнда A | значение операнда В | значение A Ú B |
| истина | Истина | истина |
| истина | Ложь | истина |
| ложь | Истина | истина |
| ложь | Ложь | ложь |
4. Импликация, логическое следование.
Обозначается знаком ®, например, A ® B
Высказывание A ® B ложно тогда и только тогда, когда А истинно, а В ложно (табл. 2.4).
Таблица 2.4
Таблица истинности операции импликация
| значение операнда A | значение операнда В | значение A ® B |
| истина | Истина | истина |
| истина | Ложь | ложь |
| ложь | Истина | истина |
| ложь | Ложь | истина |
Каким же образом импликация связывает два элементарных высказывания? Операция импликации A ® B в русском языке может быть выражена связками «если A, то B», «из A следует B», «A влечет B».
Примерами составных высказываний типа A ® B могут быть «Если нет дождя, то нет урожая» (A – «Нет дождя», B – «Нет урожая»), «Если данный четырёхугольник квадрат, то около него можно описать окружность» (А – «данный четырёхугольник — квадрат», B – «около данного четырёхугольника можно описать окружность»).
Рассмотрим последнее высказывание. Имеются следующие варианты:
I. А истинно, и В истинно. Утверждается, что данный четырёхугольник квадрат, и около него можно описать окружность. Поскольку вокруг квадрата всегда можно описать окружность, то имеем верное логическое заключение, результат операции импликация – «истина».
II. А ложно, то есть данный четырёхугольник не является квадратом. В этом случае мы не можем однозначно утверждать, можно или нельзя описать возле него окружность (вокруг некоторых четырехугольников можно описать окружность, вокруг других – нет, и то, и другое утверждение может быть истинным).
То есть, если A – ложно, то нельзя судить об истинности B.
Поэтому при условии, что A принимает значение «ложь» и при любом значении B, все выражение A ® B остается истинным. Результат операции импликация – «истина».
III. A истинно, а B ложно. Утверждается, что вокруг квадрата нельзя описать окружность. Имеем неверное, ложное логическое заключение, результат операции импликация – «ложь».
5. Эквивалентность, двойная импликация.
Для обозначения эквивалентности используется знак «.
Высказывание A «B истинно тогда и только тогда, когда значения А и В совпадают (табл. 2.5).
Таблица 2.5
Таблица истинности операции эквивалентно
| значение операнда A | значение операнда В | значение A «B |
| истина | Истина | Истина |
| истина | Ложь | Ложь |
| ложь | Истина | Ложь |
| ложь | Ложь | Истина |
На русском языке эквивалентность выражается связками «тогда и только тогда», «необходимо и достаточно», «равносильно».
Например, высказывания «24 делится на 6 тогда и только тогда, когда 24 делится на 3» и «24 не делится на 6 тогда и только тогда, когда 24 не делится на 3» истинны, а высказывания «24 делится на 6 тогда и только тогда, когда 24 делится на 5» и «21 не делится на 6 тогда и только тогда, когда 21 делится на 3» ложны.
Порядок выполнения логических операций задается круглыми скобками. Любое выражение в скобках вычисляется раньше, чем выполняется операция, предшествующая скобкам.
Общий порядок вычисления логического выражения – слева направо, с учетом приоритета выполнения логических операций. Сначала выполняются те операции, которые имеют более высокий приоритет.
Приоритеты (порядок выполнения) логических операций:
· отрицание,
· конъюнкция (логическое умножение),
· дизъюнкция (логическое сложение),
· импликация (следование),
· эквивалентность.
Таким образом, запись выражения Ø А Ù В Ú С Ù D совпадает с записью ((Ø А)Ù В) Ú (СÙ D). Возможна запись А Ù В Ù С вместо (А Ù В) Ù С. То же относится и к дизъюнкции: возможна запись А Ú В Ú С вместо (А Ú В) Ú С.
В компьютерной отрасли часто используется еще одна логическая операция, напоминающая дизъюнкцию, – это исключающее или, которая не является основной и чаще всего обозначается словом XOR. Высказывание, полученное с помощью данной операции, принимает значение истина при условии, что один, и только один, из его операндов истинен (табл. 2.6).
В разговорной речи операции исключающее или соответствуют конструкции «или …, или …», «либо …, либо …». Например, «Либо я пойду на футбольный матч, либо буду смотреть его прямую трансляцию дома по телевизору». Очевидно, что истинность одной части этого предложения исключает истинность другой.
Можно сказать, что операция исключающее или служит для проверки совпадения значений ее операндов. Результат истинен только в том случае, если значения операндов различны, и ложен, если значения операндов совпадают.
Таблица 2.6
Таблица истинности операции «исключающее ИЛИ»
| значение операнда A | значение операнда В | значение A xor B |
| истина | Истина | Ложь |
| истина | Ложь | Истина |
| ложь | Истина | Истина |
| ложь | Ложь | Ложь |
Можно проверить, что выражение A xor B может быть выражено через основные логические операции, то есть эквивалентно логическому выражению AÙØBÚØAÙB.
Пример: Для каких наборов значений: 1. a=0, b=3, c=5, 2. a=1, b=7, c=2, 3. a=3, b=2, c=7, 4. a=2, b=0, c=3 выражение Ø (a>0) Ú (b<3) Ù (c<=5)истинно?
Последовательно подставляя наборы значений переменных в выражение, получаем:
1. Ø (0>0) Ú (3<3) Ù (5<=5)
Ø «ложь» Ú «ложь» Ù «истина» – «истина»;
2. Ø (1>0) Ú (7<3) Ù (2<=5)
Ø «истина» Ú «ложь» Ù «истина» – «ложь»;
3. Ø (3>0) Ú (2<3) Ù (7<=5)
Ø «истина» Ú «истина» Ù «ложь» – «ложь»;
4. Ø (2>0) Ú (0<3) Ù (3<=5)
Ø «истина» Ú «истина» Ù «истина» – «истина»;
Выражение Ø (a>0) Ú (b<3) Ù (c<=5)истинно для наборов 1 и 4.
Для любого логического выражения можно составить таблицу истинности. Для выражения, содержащего n логических переменных, таблица истинности будет содержать 2n различных наборов истинностных значений. В таблицах истинности наборы значений логических переменных можно располагать как по строкам, так и по столбцам.
Пример: составить таблицу истинности выражения Ø(AÚB).
Выражение содержит 2 переменные, значит, в таблице истинности – 4 набора значений. Для сокращения записи обозначим значение «истина» единицей 1, значение «ложь» – нулем.
Таблица 2.7
Таблица истинности выражения Ø(AÚB)
| значение A | значение B | Значение Ø(AÚB) |
Пример: составить таблицу истинности выражения Ø(AÙØB)ÙØC.
Выражение содержит 3 переменные, в таблице истинности – 8 наборов значений (табл. 2.8)
Таблица 2.8
Таблица истинности выражения Ø(AÙØB)ÙØC
| Переменные | Промежуточные выражения | Результат | |||||
| A | B | C | ØB | AÙØB | Ø(AÙØB) | ØС | Ø(AÙØB)ÙØC |
Пример: соответствует ли заданная таблица истинности (табл. 2.9) какому-либо из перечисленных логических выражений: 1. XÙØY®Z, 2. XÙY®Z, 3. (XÚY)®Z, 4. ØXÙY®Z?
Таблица 2.9
Таблица истинности примера
| X | ||||||||
| Y | ||||||||
| Z | ||||||||
| Результат |
В таблице истинности для удобства пронумеруем наборы значений переменных, расположенные в столбцах таблицы.
Для решения данной задачи можно последовательно подставлять все наборы значений из таблицы в имеющиеся выражения и отсеивать те выражения, значения которых противоречат значениям, указанным в таблице.
Для сокращения перебора можно воспользоваться тем фактом, что итоговая (та, которая выполняется последней) операция во всех перечисленных выражениях – операция импликации ® дает ложное значение тогда и только тогда, когда первый операнд принимает значение «истина», а второй – «ложь».
В нашей таблице только три набора привели к ложному результату выражения – набор 3, 5 и 7.
Подставим значения набора 3 (X =«ложь», Y =«истина», Z =«ложь») в каждое из четырех выражений. Получаем: 1. «ложь» ® «ложь», 2. «ложь» ® «ложь», 3. «истина» ® «ложь», 4. «истина» ® «ложь». Значения выражений 1. и 2. – «истина», выражений 3. и 4. – «ложь». Таким образом, третьему набору из таблицы истинности соответствуют только выражения 3. и 4. Проверим их соответствие таблице истинности для следующего набора значений.
Подставим значения набора 5 (X =«истина», Y =«ложь», Z =«ложь») в выражения 3. и 4. Получаем: выражение 3. «истина» ® «ложь», 4. «ложь» ® «ложь». Значение выражения 3. – «ложь», 4. – «истина». Выражение 4. не соответствует таблице истинности.
Для того, чтобы проверить, соответствует ли таблице истинности выражение 3. надо проверить для него все остальные (ранее не проверенные) наборы значений из заданной таблицы:
набор 1: «ложь» ® «ложь», результат «истина» – соответствует;
набор 2: «ложь» ® «истина», результат «истина» – соответствует;
набор 4: «истина» ® «истина», результат «истина» – соответствует;
набор 6: «истина» ® «истина», результат «истина» – соответствует;
набор 7: «истина» ® «ложь», результат «ложь» – соответствует;
набор 8: «истина» ® «истина», результат «истина» – соответствует.
Заданная таблица истинности соответствует выражению 3. (XÚY)®Z.
Булевой функцией называется функция от n аргументов f(x1,x2,…,xn), аргументы которой и она сама принимают истинностные значения.
Логической функцией является любое логическое выражение, построенное с помощью основных логических операций: отрицания, конъюнкции, дизъюнкции. Поэтому эти операции часто также называют булевыми функциями.
Булева (пропозициональная) формула определяется правилами ее построения:
1. Всякая логическая переменная и логические константы «истина» (1) и «ложь» (0) – формулы.
2. Если А и В – формулы, то ØA, (А Ù В), (А Ú В), (А ® B), (А «В)– формулы.
3. Никаких других булевых формул нет.
Замена всех входящих в логическую формулу логических переменных произвольными истинностными значениями называется интерпретацией. Если при некоторых интерпретации формула принимает значение «истина», то такая формула называются выполнимой.
Если формула принимает значение «истина» при любых интерпретациях, такая формула называется тождественно истинной формулой или тавтологией. Таковой будет, например, формула A Ú ØA. Например, утверждение «Мяч – круглый или мяч – не круглый» всегда истинно.
В качестве другого примера рассмотрим формулу A Ù ØA, которой соответствует, например, высказывание «Катя самая высокая девочка в классе, и в классе есть девочки выше Кати». Очевидно, что эта формула всегда ложна, так как либо А, либо ØA обязательно ложно. Формулы, ложные при любых интерпретациях, называются тождественно ложными формулами или противоречиями.
Булевы формулы, содержащие переменные, называются эквивалентными (равносильными), если значения этих формул совпадают при любых интерпретациях. Эквивалентность обозначается знаком = или º.
Так, выражения A ® B и (Ø А) Ú В равносильны, а А Ú В и А Ù В – нет (значения выражений разные, например, при А =«истина», В =«ложь»).
Эквивалентность формул не нарушится, если вместо некоторой переменной подставить одну и ту же функцию или формулу.
Замена формулы другой, ей равносильной, называется равносильным (тождественным) преобразованием данной формулы.
Тождественные преобразования логических выражений позволяют в ряде случаев упростить выражения, опираясь на следующие основные законы алгебры логики (табл. 2.10):
Таблица 2.10
Основные законы алгебры логики
| Закон | для логического ИЛИ | для логического И |
| коммутативность | AÚB=BÚA | AÙB=BÙA |
| ассоциативность | AÚ(BÚC)=AÚBÚC | AÙ(BÙC)=AÙBÙC |
| дистрибутивность | AÙ(BÚC) = (AÙB)Ú(AÙC) | AÚ(BÙC)=(AÚB)Ù(AÚC) |
| двойственность | Ø(AÚB) = ØAÙØB | Ø(AÙB) = ØAÚØB |
| идемпотентность | AÚA = A | AÙA = A |
| поглощение | AÚ(AÙB) = A | AÙ(AÚB) = A |
| cклеивание | (AÙB)Ú(ØAÙB) = B | (AÚB)Ù(ØAÚB) = B |
| AÚ(ØAÙB) = AÚB | AÙ(ØAÚB) = AÙB | |
| операция переменной с ее инверсией | AÚØA = 1 | AÙØA = 0 |
| операция с константами | AÚ1 = 1, AÚ0 = A | AÙ1 = A, AÙ0 = 0 |
| отрицание констант | Ø1 = 0, Ø0 = 1 | |
| двойное отрицание | Ø(ØA)=A |
Пример 1: упростить формулу Ø(AÚB)Ù(AÙØB)
Решение:
Ø(AÚB)Ù(AÙØB) = (ØAÙØB)Ù(AÙØB) = ØAÙØBÙAÙØB =
двойственность ассоциативность коммутативность
ØAÙAÙØBÙØB = 0ÙØB = 0.
операция с инверсией, идемпотентность, операция с константой
Пример 2: упростить формулу AÚØ(BÙØC)ÚØ(ØAÚBÚØC)
Решение:
AÚØ(BÙØC)ÚØ(ØAÚBÚØC) = AÚ(ØBÚØØC)Ú(ØØAÙØBÙØØC) =
двойственность двойное отрицание
AÚØBÚCÚ(AÙØBÙC) = AÚØBÚ(CÚ(AÙØBÙC)) =
ассоциативность коммутативность
AÚØBÚ(CÚ(CÙAÙØB)) = AÚØBÚ(CÚ(CÙ(AÙØB))) = AÚØBÚC.
ассоциативность поглощение
Пример 3: Составить логические выражения, истинные только при выполнении указанных условий
а) x принадлежит отрезку [a,b].
Ответ: (x >= a) Ù (x <= b)
б) x лежит вне отрезка [a,b].
Ответ: (x < a) Ú (x > b).
в) x лежит выше прямой y = -x во второй и четвертой четвертях прямоугольной системы координат.
Ответ: (y > -x) Ù (x < 0 Ú y < 0).
Пример 4: Для какого числа X истинно высказывание
(X>2) → (X>5)?
Решение:
Составим таблицу истинности (табл. 2.11) для (X>2) → (X>5)
Проанализируем те строки, где импликация истинна. При этом значения аргументов зададим неравенствами (табл. 2.12).
Таблица 2.11
Таблица истинности примера 4
| X>2 | X>5 | (X>2) → (X>5) |
Таблица 2.12
Таблица решения примера 4
| Аргументы | Функция | Общая область аргументов | |
| X<=2 | X<=5 | X<=2 | |
| X<=2 | X>5 | – | |
| – | – | – | – |
| X>2 | X>5 | X>5 |
Таким образом, область значений X, при которых импликация истинна, будет: (X <= 2) Ú (X > 5).






