Числа могут быть представлены в различных системах счисления.
Система счисления – совокупность приемов и правил записи чисел с помощью набора определенных символов.
Для записи чисел могут использоваться не только цифры, но и буквы (например, запись римских цифр - XXI, MCMXCIX). В зависимости от способа изображения чисел системы счисления делятся на позиционные и непозиционные.
В позиционной системе счисления количественное значение каждой цифры числа зависит от того, в каком месте (позиции или разряде) записана та или иная цифра этого числа. Позиции числа нумеруют от 0 справа налево. Например, меняя позицию цифры 2 в десятичной системе счисления, можно записать разные по величине десятичные числа, например, 2 (цифра 2 стоит на 0-й позиции и означает две единицы); 20 (цифра 2 стоит на 1-й позиции и означает два десятка); 2000 (цифра 2 стоит на 3-й позиции и означает две тысячи); 0,02 и т.д. Перемещение положения цифры в соседний разряд увеличивает (уменьшает) ее значение в 10 раз.
В непозиционной системе счисления цифры не изменяют своего количественного значения при изменении их расположения (позиции) в числе. Примером непозиционной системы может служить римская система, в которой независимо от местоположения, одинаковый символ имеет неизменное значение (например, символ X в числе XVX означает десять, где бы он ни стоял).
Количество (p) различных символов, используемых для изображения числа в позиционной системе счисления, называется основанием системы счисления. Значения цифр лежат в пределах от 0 до p-1.
В десятичной системе счисления p=10 и для записи любого числа используется 10 цифр: 0, 1, 2,... 9.
Для компьютера наиболее подходящей и надежной оказалась двоичная система счисления (p=2), в которой для представления чисел используются последовательности цифр - 0 и 1. Кроме того, для работы компьютера оказалось удобным использовать представление информации с помощью еще двух систем счисления:
· восьмеричной (p=8, т.е. любое число представляется с помощью 8 цифр - 0,1, 2,...7);
· шестнадцатеричной (p=16, используемые символы - цифры - 0, 1, 2,..., 9 и буквы - A, B, C, D, E, F, заменяющие числа 10,11, 12, 13, 14, 15 соответственно).
Соответствие кодов десятичной, двоичной и шестнадцатеричной систем счисления представлено в таблице 2.
Таблица 2. Соответствие кодов десятичной, двоичной и шестнадцатеричной систем счисления
| Десятичная | Двоичная | Шестнадцатеричная |
| A | ||
| B | ||
| C | ||
| D | ||
| E | ||
| F |
В общем случае любое число N в позиционной системе счисления можно представить в виде:
(1),
где k - количество разрядов в целой частности числа N;
- (k –1)-ая цифра целой части числа N, записанного в системе счисления с основанием p;
- n-ая цифра дробной части числа N, записанного в системе счисления с основанием p;
n - количество разрядов в дробной части числа N;
Максимальное число, которое может быть представлено в к разрядах 
.
Минимальное число, которое может быть представлено в n разрядах 
.
Имея в целой части числа к разрядов, а в дробной n разрядов, можно записать всего 
разных чисел.
С учетом этих обозначений запись числа N в любой позиционной системе счисления с основанием p имеет вид:
Пример 8
При p = 10 запись числа в десятичной системе счисления – 2466,675 10, где k = 4, n = 3.
При p = 2 запись числа в двоичной системе – 1011,112, где k = 4, n = 2.
Двоичная и шестнадцатеричная системы счисления обладают такими же свойствами, что и десятичная, только для представления чисел используется не 10 цифр, а всего две в первом случае и 10 цифр и 6 букв во втором случае. Соответственно и разряд числа называют не десятичным, а двоичным или шестнадцатеричным. Основные законы выполнения арифметических действий в двоичной и шестнадцатеричной системах счисления соблюдаются точно также как и в десятичной.
Для сравнения рассмотрим представление чисел в разных системах счисления, как сумму слагаемых, в которых учтен вес каждого разряда.
Пример 9
В десятичной системе счисления
В двоичной системе счисления
В шестнадцатеричной системе счисления
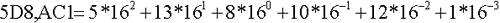
Существуют правила перевода чисел из одной системы счисления в другую.
