Синтаксические меры количества информации имеют дело с обезличенной информацией, не выражающей смыслового отношения к объекту.
Объем данных 
в сообщении измеряется количеством символов (разрядов) в этом сообщении. В различных системах счисления один разряд имеет различный вес, и соответственно меняется единица измерения данных:
· в двоичной системе счисления единица измерения - бит (binary digit - двоичный разряд). Наряду с этой единицей измерения широко используется укрупненная единица измерения “байт”, равная 8 бит.
· в десятичной системе счисления единица измерения - дит (десятичный разряд).
Пример 3
Сообщение в двоичной системе в виде восьмиразрядного двоичного кода 10111011 имеет объем данных 
Сообщение в десятичной системе в виде шестиразрядного числа 275903имеетобъемданных 
Определение количества информации I на синтаксическом уровне невозможно без рассмотрения понятия неопределенности состояния системы (энтропии системы). Действительно, получение информации о какой-либо системе всегда связано с изменением степени неосведомленности получателя о состоянии этой системы. Рассмотрим это понятие.
Пусть до получения информации потребитель имеет некоторые предварительные (априорные) сведения о системе a. Мерой его неосведомленности о системе является функция Н(a), которая в тоже время служит и мерой неопределенности состояния системы. Эта мера получила название энтропия. Если потребитель имеет полную информацию о системе, то энтропия равна 0. Если потребитель имеет полную неопределенность о какой-то системе, то энтропия является положительным числом. По мере получения новой информации энтропия уменьшается.
После получения некоторого сообщения b получатель приобрел некоторую дополнительную информацию 
, уменьшившую его априорную неосведомленность так, что апостериорная (после получения сообщения b) неопределенность состояния системы стала 
.
Тогда количество информации о системе, полученное в сообщении b, определится как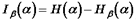 
, т. е. количество информации измеряется изменением (уменьшением) неопределенности состояния системы.
Если конечная неопределенность обратится в нуль, то первоначальное неполное знание заменится полным знанием и количество информации 
. Иными словами, энтропия системы Н(a) может рассматриваться как мера недостающей информации.
Энтропия системы Н(a), имеющая N возможных состояний, согласно формуле Шеннона, равна
(1)
где 
- вероятность того, что система находится в i -м состоянии.
Для случая, когда все состояния системы равновероятны, т.е. их вероятности равны 
, ее энтропия определяется соотношением
(2)
Энтропия системы в двоичной системе счисления измеряется в битах. Исходя из формулы (2) можно сказать, что в системе в равновероятными состояниями 1 бит равен количеству информации, которая уменьшает неопределенность знаний в два раза.
Пример 4
Система, которая описывает процесс бросания монеты, имеет два равновероятных состояния. Если вам нужно угадать, какая сторона выпала сверху, то вы сначала имеете полную неопределенность о состоянии системы. Что бы получить информацию о состоянии системы, вы задаете вопрос: "Это орел?". Этим вопросом вы пытаетесь отбросить половину неизвестных состояний, т.е. уменьшить неопределенность в 2 раза. Какой бы ответ ни последовал "Да" или "Нет", вы получите полную ясность о состоянии системы. Таким образом, ответ на вопрос содержит 1 бит информации. Поскольку после 1-го вопроса наступила полня ясность, то энтропия системы равна 1. Этот же ответ дает формула (2), т.к. log22=1.
Пример 5.
Игра "Отгадай число". Вам надо угадать задуманное число от 1 до 100. В начале отгадывания вы имеете полную неопределенность о состоянии системы. При отгадывании надо задавать вопросы не хаотично, а так, чтобы ответ уменьшал неопреденность знаний в 2 раза, получая таким образом примерно 1 бит информации после каждого вопроса. Например, сначала надо задать вопрос: "Число больше 50?". "Правильный" подход к отгадыванию дает возможность угадать число за 6-7 вопросов. Если применить формулу (2), то получится, что энтропия системы равна log2100=6,64.
Пример 6.
Алфавит племени "тумбо-юмбо" содержит 32 различных символа. Какова энтропия системы? Другими словами надо определить, какое количество информации несет в себе каждый символ.
Если считать, что каждый символ встречается в словах с равной вероятностью, то энтропия log232=5.
Наиболее часто используются двоичные и десятичные логарифмы. Единицами измерения в этих случаях будут соответственно бит и дит.
Коэффициент (степень) информативности (лаконичность) сообщения определяется отношением количества информации к объему данных, т.е.
,
причем 
.
Чем больше коэффициент информативности Y, тем меньше объем работы по преобразованию информации (данных) в системе. Поэтому стремятся к повышению информативности, для чего разрабатываются специальные методы оптимального кодирования информации.
