Как и в предыдущем случае, изучается влияние двух факторов на некоторую переменную. Отличие состоит в том, что для каждой комбинации уровней имеется более одного наблюдения. Ограничимся простейшим случаем двух наблюдений для каждой комбинации уровней. В этом случае таблица исходных данных содержит по два наблюдения в каждой ячейке. Большее количество наблюдений позволяет рассматривать более сложную модель, учитывающую возможное взаимодействие факторов. Модель имеет вид:
.
Здесь 
общее среднее значение; 
"чистые" (без учета взаимодействия) эффекты факторов А и В; 
эффекты взаимодействия факторов; 
случайные ошибки (они удовлетворяют тем же условиям, что и в предыдущих пунктах).
Методом наименьших квадратов находят оценки параметров модели. 
.
Далее для дисперсионного анализа нужно вычислить следующие суммы квадратов.
.
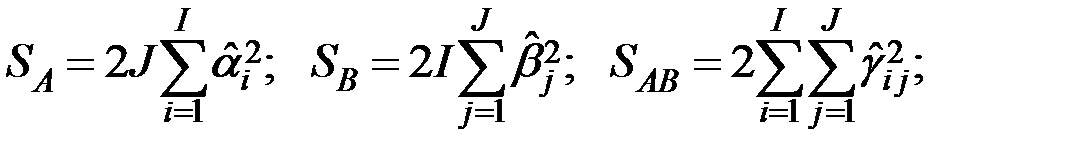
Делим эти суммы на соответствующие числа степеней свободы.
.
Результаты дисперсионного анализа удобно представлять в виде следующей таблицы.
Таблица 8. Результаты дисперсионного анализа
| Источник именчивости | Суммы квадратов | Степени свободы | Средние суммы квадратов | F -отношение |
| фактор А | 
| 
| 
| 
|
| фактор В | 
| 
| 
| 
|
| взаимо-действие факторов |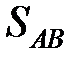 
| 
| 
| 
|
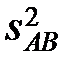
| ошибка эксперимента | 
| 
| 
| – |
| – | 
| 
| – | – |
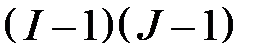
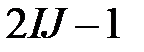
Проверяются три гипотезы:
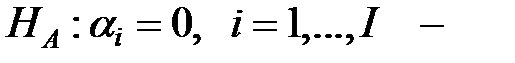фактор А не влияет на у;
фактор В не влияет на у;
взаимодействие факторов отсутствует.
Пример.
Таблица 9. Исходные данные 
.
| В А | ||||
| 2,38; 2,68 | 2,61; 2,89 | 2,87; 3,03 | 2,82; 2,46 | |
| 4,20; 4,12 | 3,96; 4,02 | 5,09; 4,85 | 4,78; 5,22 | |
| 5,52; 5,98 | 4,15; 5,05 | 5,42; 5,64 | 5,29; 5,87 |
Таблица 10. Средние значения 
| В А | Средние по строкам | ||||
| 2,53 | 2,40 | 2,55 | 2,64 | 2,53 | |
| 4,16 | 4,64 | 4,97 | 5,00 | 4,69 | |
| 5,75 | 4,90 | 5,53 | 5,58 | 5,44 | |
| Средние по столбцам | 4,15 | 3,98 | 4,35 | 4,41 | 4,22 |
Таблица 11. Дисперсионный анализ
| Источник именчивости | Суммы квадратов | Степени свободы | Средние суммы квадратов | F -отношение |
| фактор А | 
| 
| 
| 
|
| фактор В |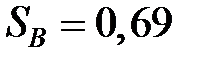 
| 
| 
| |
| взаимодействие факторов | 
| 
| 
| |
| ошибка эксперимента | 
| 
| – | |
| – | 
| – | – |
Находим из таблицы F - распределения критические значения при α = 0,05 и степенях свободы (2; 12), (3; 12) и (6; 12) и сравниваем их с рассчитанными.
Получаем:
гипотеза 
- гипотеза отвергается;
гипотеза 
- гипотеза принимается;
гипотеза 
- гипотеза отвергается.
Выводы:
· фактор А влияет на переменную у;
· фактор В при фиксированном уровне фактора А не влияет на пере-менную у;
· действие фактора В проявляется в том, что степень влияния фактора А зависит от того, на каком уровне находится фактор В.
Замечание.
В данном примере рассчитанные значения F значительно отличаются от критических, поэтому даже заметное изменение уровня значимости не отменит сделанных выводов. При других данных тот или иной выбор значения 
может существенно повлиять на выводы. Предположим, например, что мы получили рассчитанное значение 
, равное 
вместо 
. Тогда, выбрав большее значение 
, получим меньшее значение 
. В этом случае гипотезу 
в соответствии с правилом пришлось бы отвергнуть.
Библиографический список
1. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 1979.
2. Смирнов Н.В., Дунин-Барковский И.В. Курс теории вероятностей и математической статистики (для технических приложений). – М.: Наука, 1969.
3. Планирование эксперимента в исследовании технологических процессов. – М.: Мир, 1977.
Приложение. Варианты индивидуальных заданий по теме: "Двухфакторный дисперсионный анализ с однократными наблюдениями".
| вариант 1 B1 B2 B3 B4 A1 0.96 1.04 0.40 -0.03 A2 0.87 -0.04 -0.46 0.11 A3 0.27 0.97 0.35 -0.81 | вариант 2 B1 B2 B3 B4 A1 2.68 3.29 2.88 4.45 A2 4.12 4.96 5.09 5.22 A3 5.52 4.50 5.42 5.29 |
| вариант 3 B1 B2 B3 B4 A1 1.08 2.52 1.75 2.65 A2 1.80 2.42 2.13 3.78 A3 1.83 2.42 2.65 3.00 | вариант 4 B1 B2 B3 B4 A1 1.80 2.14 1.63 0.86 A2 3.96 1.81 1.41 2.05 A3 5.00 4.48 2.61 3.19 |
| вариант 5 B1 B2 B3 B4 A1 3.11 1.61 2.72 2.68 A2 3.40 2.76 3.21 2.82 A3 5.20 4.36 4.97 5.60 | вариант 6 B1 B2 B3 B4 A1 1.90 1.59 0.98 1.66 A2 4.22 2.21 2.77 1.45 A3 4.30 4.16 4.11 2.60 |
| вариант 7 B1 B2 B3 B4 A1 0.71 1.23 0.22 0.30 A2 3.53 1.71 2.72 2.17 A3 2.97 3.88 2.26 3.40 | вариант 8 B1 B2 B3 B4 A1 1.68 1.86 1.57 2.17 A2 1.70 2.92 2.10 2.07 A3 2.34 2.93 3.94 4.22 |
| вариант 9 B1 B2 B3 B4 A1 2.91 1.87 2.23 2.43 A2 4.16 3.63 5.08 5.11 A3 4.38 4.62 5.01 6.00 | вариант 10 B1 B2 B3 B4 A1 0.71 1.32 2.14 2.81 A2 3.01 2.51 2.16 2.77 A3 3.52 2.24 3.37 4.14 |
| вариант 11 B1 B2 B3 B4 A1 3.60 3.62 3.51 3.33 A2 3.90 5.41 5.18 4.56 A3 6.38 6.21 7.01 7.72 | вариант 12 B1 B2 B3 B4 A1 1.52 2.42 2.19 2.51 A2 2.66 2.73 3.68 4.99 A3 4.18 5.54 4.56 4.87 |
| вариант 13 B1 B2 B3 B4 A1 2.36 2.70 3.41 2.75 A2 4.04 4.40 4.81 3.46 A3 4.83 4.61 6.07 6.40 | вариант 14 B1 B2 B3 B4 A1 0.47 2.17 1.51 1.93 A2 1.44 1.55 2.06 2.22 A3 2.96 3.03 2.55 2.75 |
| вариант 15 B1 B2 B3 B4 A1 1.84 2.24 0.64 1.50 A2 3.04 2.25 1.91 1.21 A3 4.78 3.81 4.03 3.33 | вариант 16 B1 B2 B3 B4 A1 1.07 2.07 1.00 -0.71 A2 1.54 2.85 2.15 1.28 A3 3.28 3.04 1.72 1.12 |
| вариант 17 B1 B2 B3 B4 A1 2.78 3.29 3.33 3.13 A2 3.35 3.94 3.48 4.15 A3 3.04 5.13 4.28 5.46 | вариант 18 B1 B2 B3 B4 A1 3.18 2.75 3.49 3.36 A2 4.08 4.48 4.71 5.16 A3 5.10 6.06 6.20 5.75 |
| вариант 19 B1 B2 B3 B4 A1 1.86 0.93 0.66 0.65 A2 3.27 2.37 2.55 1.80 A3 3.82 3.40 4.47 4.42 | вариант 20 B1 B2 B3 B4 A1 1.01 0.30 1.09 0.79 A2 1.25 0.68 1.64 -0.09 A3 0.58 0.46 0.46 0.03 |
| вариант 21 B1 B2 B3 B4 A1 1.47 1.40 0.77 0.36 A2 2.96 2.05 2.76 2.42 A3 2.08 3.15 3.35 3.34 | вариант 22 B1 B2 B3 B4 A1 1.60 1.47 0.36 1.32 A2 4.18 3.59 3.95 2.44 A3 6.31 5.26 5.41 4.59 |
| вариант 23 B1 B2 B3 B4 A1 3.13 1.81 3.71 2.11 A2 2.86 3.63 4.72 3.25 A3 4.44 4.73 4.78 5.61 | вариант 24 B1 B2 B3 B4 A1 2.46 2.18 2.43 1.33 A2 3.17 4.25 2.67 2.07 A3 4.45 5.48 4.08 3.66 |
Содержание
1. Основные задачи………………………………………………………………….3
2. Предварительные сведения………………………………………………………3
3. Однофакторный дисперсионный анализ………………………………………..4
4. Двухфакторный дисперсионный анализ с однократными наблюдениями …..9
5. Двухфакторный анализ с многократными наблюдениями…………………...13
Библиографический список……………………………………………………….16
Приложение………………………………………………………………………...16
