Однофакторный дисперсионный анализ

Элементы дисперсионного анализа

Цель данных методических указаний – познакомить студентов с простейшими задачами, решаемыми средствами дисперсионного анализа, и помочь в выполнении индивидуального задания.

Основные задачи

Предположим, что изучается влияние одного или нескольких факторов на некоторую величину. Эти факторы могут принимать разные значения, называемые уровнями. Факторы могут быть как числовыми, так и нечисловыми. Например, на износ автомобильных покрышек может влиять как тип покрышки (нечисловой фактор), так и длина пробега (числовой фактор).

Вот некоторые из задач, которые ставятся в дисперсионном анализе:

· влияет ли некоторый фактор или группа факторов на изучаемую величину?

· какой из них имеет наибольшее влияние?

· зависит ли влияние факторов от их взаимодействия друг с другом?

 

Предварительные сведения

Напомним определения некоторых понятий из курса теории вероятностей и математической статистики, необходимых для понимания последующего материала:

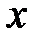а) Функция называется функцией распределения случайной величины , если для любого выполняется равенство , где вероятность попадания значения величины в интервал .
б) Функция называется плотностью распределения.

в) Числовые характеристики случайной величины:

математическое ожидание;
дисперсия.

Математическое ожидание является в определенном смысле средним значением случайной величины, а дисперсия – характеристикой рассеяния значений случайной величины относительно ее среднего значения.

г) Число , определяемое уравнением , называется - квантилью распределения. Из определения следует, что -квантиль является возрастающей функцией от . Если график плотности симметричен относительно математического ожидания , то 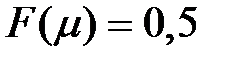и, значит, в этом случае совпадает с -квантилью.

д) Случайной выборкой объема называется набор значений случайной величины, полученных в результате независимых опытов. Эти значения называют в статистике наблюдениями.

е) Функция от наблюдений называется несмещенной оценкой параметра , если ее математическое ожидание равно .

Однофакторный дисперсионный анализ

1. Постановка задачи

Пусть фактор А имеет m уровней и число получено в результате j -го опыта, проведенного на его i-м уровне, . Числа называются наблюдениями, а число наблюдений, полученных на i-м уровне. Наблюдения представим в виде

, (1)
где - математическое ожидание у на i-м уровне, а - случайная ошибка. Обычно наблюдения записывают в виде таблицы.

 

Таблица 1. Исходные данные

 

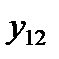
Отметим, что столбцы в таблице могут быть разной длины, так как число наблюдений на разных уровнях фактора А не обязательно одинаково.

Пример 1. Четыре фирмы производят одинаковые изделия, некоторый показатель качества изделия (например, время безотказной работы). Здесь фактор А нечисловой – это фирма-производитель. Для сравнения качества изделий отбирают по 7 изделий у двух фирм и 9 и 8 изделий у двух других фирм и определяют значение для каждого изделия. Получаем две случайные выборки объема 7 и две – объема 9 и 8. Здесь m = 4, n₁ = 9, n₂ = n₃ = 7, n₄ = 8. Требуется на основании этих данных выяснить, одинаково ли качество продукции у этих фирм, т.е. ответить на первый из перечисленных выше вопросов.

Если фактор не влияет на переменную у, торассеяние ее значений вызвано лишь случайными ошибками, а математические ожидания на всех уровнях одинаковы. В терминах математической статистики задача сводится к проверке гипотезы .

Обозначим . Число называется эффектом фактора А на i -м уровне. Тогда уравнение (1) и гипотеза принимают вид
(2)
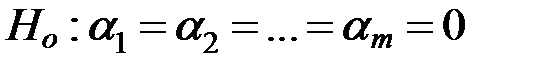. (3)
Далее предполагается, что случайные ошибки удовлетворяют следующим условиям:

а) имеют нулевое математическое ожидание;

б) имеют постоянную дисперсию, т.е. не зависящую ни от уровня фактора, ни от номера наблюдения;

в) подчиняются нормальному распределению.

2. Оценки параметров модели (2)
Определим следующие величины:
средние значения по столбцам;
отклонения от среднего в каждом столбце;
общее среднее, ;

отклонения средних по столбцам от общего среднего;
Если выполнены допущения а), б), в), то можно доказать, что

, (4)
где .

На языке математической статистики соотношения (4) означают, что случай-ные величины и являются несмещенными оценками параметров и . 3. Идея проверки гипотезы (3)
Вычислим следующие суммы квадратов:

полная сумма квадратов;

межгрупповая сумма квадратов;

внутригрупповая сумма квадратов.

Справедливо соотношение

. (5)
Здесь характеризует рассеяние средних по столбцам относительно общего среднего, т.е. рассеяние между группами (уровнями фактора), а характеризует рассеяние значений относительно , т.е. рассеяние внутри групп (столбцов таблицы).

Метод проверки гипотезы (3) основан на следующей идее. Если гипотеза верна, т.е. , то величины должны быть достаточно близки к 0. Тогда вклад в по сравнению с должен быть мал. Поэтому малое значение является доводом в пользу гипотезы, а большое значение является доводом против гипотезы. Очевидно, в этом рассуждении не хватает точного указания, какое значение считать малым.

4. Применение F - критерия для проверки гипотезы

Опишем точный метод проверки гипотезы (3), основанный на - критерии.

1. Вычисляем средние суммы квадратов:

Числа (m – 1) и (n – m), на которые делятся суммы квадратов, назы-ваются степенями свободы.

2. Вычисляем значение - критерия

.

3. Задаем число и из таблицы квантилей - распределения со степенями свободы при уровне значимости 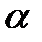находим критическое значение .

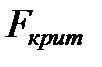Правило:
если , то гипотеза отвергается;

если , то гипотеза принимается.

Замечания.

1) Вероятностный смысл 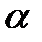состоит в следующем. Предположим, что гипотеза 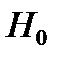верна, но из-за случайных ошибок вычисленное значение F оказалось больше критического, т.е. . Тогда согласно сформулированному выше правилу мы должны отвергнуть 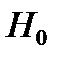, хотя на самом деле она верна. Получается, что, применяя это правило, мы в этом случае совершим ошибку, называемую ошибкой 1-го рода (отвергается верная гипотеза). Вероятность такой ошибки равна вероятности неравенства , вычисленной в предположении верности гипотезы 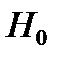, т.е. равна .

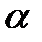2) зависит от выбранного значения 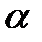, причем увеличивается при уменьшении 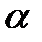. Поэтому, уменьшая 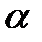, всегда можно добиться выполнения неравенства и тем самым принятия гипотезы. Однако, уменьшая 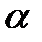, мы увеличиваем вероятность ошибки 2-го рода: принять 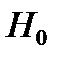, когда на самом деле она неверна. Обычно используют . Задать значение мы не можем, так как оно зависит от неизвестных нам истинных значений эффектов .

Пример 2.

Таблица 2. Исходные данные к примеру 2

Номер наблюдения	А1	А2	А3	А4
	9,57	11,17	12,07	13,12
	8,33	10,81	11,06	10,81
	10,13	11,73	10,90	12,36
	10,29	10,41	10,17	12,75
	8,85	13,18	11,29	9,91
	11,19	10,86	9,66	10,06
	11,19	11,11	11,71	12,07
	9,96	-	-	11,10
	10,33	-	-	-
	9,98	11,32	10,98	11,52

 

Здесь

Из таблицы видно, что средние по столбцам заметно различаются. Однако нельзя исключить, что это различие вызвано лишь случайным рас-сеянием данных, в то время как "истинные" значения средних, т.е. , одина-ковы. Для проверки гипотезы применим описанный выше метод. Результаты расчетов приведены в таблице 3.

Таблица 3. Результат дисперсионного анализа

Источник рассеяния	Сумма квадратов	Степени свободы	Средняя сумма квадратов
между группами	12,003		4,001	3,99	0,018

Окончание табл. 3

Источник рассеяния	Сумма квадратов	Степени свободы	Средняя сумма квадратов
внутри групп	27,047		1,002	-	-
полная	39,05		-	-	-

 

Поясним содержание таблицы. Второй столбец содержит суммы квадратов , смысл которых указан в первом столбце; в 3-м столбце – степени свободы, равные (m - 1), (n - m) и (n - 1) соответственно; 4-й столбец получается делением сумм квадратов на их степени свободы. В последний столбец обычно помещают вероятность . Дело в том, что для проверки неравенства

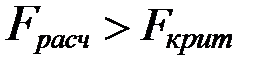(6)

потребуется сначала найти , а для этого нужна таблица квантилей F -распределения, которая не всегда доступна. Заметим, что где функция распределения Фишера. Функция возрастающая, поэтому неравенство (6) равносильно (7)

. (7)

Поэтому вместо неравенства (6) можно пользоваться неравенством (7). В данном примере при получаем принимается на уровне значимости 0,05.