Факторный анализ – комплексное и системное изучение и измерение воздействия факторов на величину результативных показателей.
Виды факторного анализа:
· детерминированный (функциональный) и стохастический (корреляционный) факторный анализ;
· прямой и обратный (дедуктивный и индуктивный) факторный анализ;
· одноступенчатый и многоступенчатый анализ;
· статистический и динамический факторный анализ;
· ретроспективный и перспективный факторный анализ.
Основные задачи факторного анализа:
- отбор факторов, которые определяют исследование нормативного показателя;
- их классификация и систематизация с целью обеспечения возможности системного подхода;
- определение формы зависимости между факторами и результативным показателем;
- моделирование взаимосвязей между результативным и факторным показателями;
- расчет влияния факторов и оценка роли каждого из них в изменении величины результативного показателя;
- работа с факторной моделью, т.е. ее практическое использование для управления экономическими процессами.
Этапы экономического анализа:
1. Уточняются объекты, цель и задачи анализа;
2. Разрабатывается система аналитических и синтетических показателей с помощью которых характеризуется объект анализа;
3. Собирается необходимая для анализа информация, проверяется её точность и достоверность, приводится в сопоставимый вид.
4. Проводится сравнительный анализ, т.е. фактические результаты сравниваются с базовыми. Базовыми показателями могут быть:
· результаты предшествующих периодов;
· показатели конкурентов;
· нормативные, плановые показатели и т.д.
5. Выполняется факторный анализ. Выделяются факторы и определяется их влияние на результат, для чего необходимо построить аналитическую факторную модель.
6. Выявляются неиспользованные и перспективные резервы повышения эффективности хозяйственной деятельности предприятия.
7. Проводится оценка результатов хозяйствования и разработка мероприятий по исполнению выявленных резервов.
Типы факторных моделей:
· Аддитивные: результат рассчитывается как сумма показателей:
,
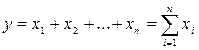· Мультипликативные: результат рассчитывается как произведение показателей:
· Кратные, результат рассчитывается как частное двух показателей:
· Смешанные, например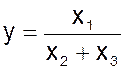 
- рентабельность производственного капитала;
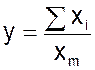- среднегодовая стоимость капитала.
Метод цепных подстановок.
Метод цепных подстановок является универсальным методом, используется для всех типов детерминированных факторных моделей. Позволяет определить влияние отдельных факторов на изменение величины результативного показателя путем постепенной замены базисной величины каждого фактора на его фактическую величину.
Замена начинается всегда с основного количественного фактора (если их несколько, то сначала берут фактор I уровня – самый независимый фактор, затем более низкого и т.д.) и заканчивается качественным показателем.
Количественные показатели – характеризуют экстенсивность использования объекта, существуют независимо от анализируемых явлений и могут быть получены путем прямого счета или непосредственного учета (например, количество рабочих, количество станков…)
Качественные показатели – отражают сравнительную характеристику анализируемого явления, характеризуют интенсивность использования количественного фактора, показывают существенные особенности и свойства изучаемых объектов (например, рентабельность, почасовая зарплата).
Изменение количественных показателей всегда приведет к изменению качественных и наоборот. Влияние каждого фактора определяется последовательными шагами. За один шаг можно сделать только одну замену. Алгебраическая сумма влияния факторов должна быть равна общему приросту результативного показателя.
Техника применения метода цепных подстановок в общем виде:
y = а × b × c
y 0 = а 0 × b 0 × c 0 – базовые значения
y 1 = а 1 × b 1 × c 1 – фактические значения
Абсолютный общий прирост результативного показателя:
D у = у 1 – у 0.
Влияние на прирост результативного показателя изменения фактора а определяется следующим образом:
у ¢ = а 1 × b 0 × c 0
D уа = y ¢ – у 0
Влияние на прирост результативного показателя изменения фактора b определяется следующим образом:
y ² = а 1 × b 1 × c 0
D уb = y ² – у ¢
Влияние на прирост результативного показателя изменения фактора с определяется следующим образом:
D ус = y 1 – y ²
После определения влияния факторов необходимо провести проверку:
D уа + D уb + D ус = D у
3.2. Метод абсолютных разниц
Используется только в мультипликативных моделях.
Величина влияния факторов рассчитывается умножением абсолютного прироста исследуемого фактора на фактическую величину факторов, которые находятся в модели слева от него, на базовую величину факторов, которые находятся справа.
1) D уа = D а × b 0 × c 0
2) D уb = D b × а 1 × c0
3) D ус = D с × а 1 × b 1
3.3. Метод относительных разниц
Применяется в моделях мультипликативного типа:
1) Рассчитываются относительные отклонения факторных показателей.
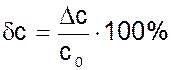
2) Отклонения результативного показателя за счет изменения каждого фактора определяется следующим образом:
Метод относительных разниц удобно применять в тех случаях, когда требуется рассчитать влияние большого количества факторов, поскольку значительно сокращается объем вычислений.
