Задачі
Для заданих формул булєвих функцій і формул, отриманих із заданих у результаті перекладу в булєв базис, довільної (по властивостях 1-18) мінімізації, синтезувати логічні схеми й оцінити їх по складності:
[(x2®x1)~x3]+(x4 /x1);
ù(ùx1~(ùx2+x3))(x1®x4);
(x1+ùx2)x3+(ùx3+ùx4)(ùx1+x3ùx4);
ù(x1+ù(x1x2x3+ùx3));
x1x2+ù(x2x3+x1+ùx2ùx3);
ù(x1ùx2)ù(x1ùx3+(x3x4));
x1ùx3+ù(x1ùx2+ùx1x3)+x2x3x4(x1+ùx1x2x3);
(x1Åx2)x3+(x1Åx3)x2;
(x1¯x2)/x3+(ùx2®x3)¯x4;
ù((x1+ùx2+x3+x4)(x1+x2+x3+ùx4))+(x1x3x4®0).
Перевести формулу ((x2®x1)~x3)Å(x4¯x1) у заданий базис і синтезувати в ньому логічні схеми:
{Ú, ù};
{Ù, ù};
{®, 0};
{, ù};
{Å, 1, Ú};
{¯};
{/}.
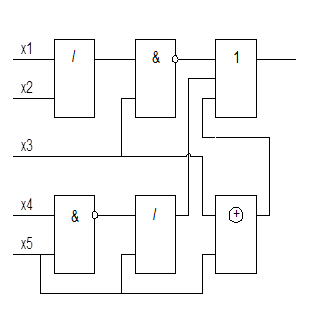 |  |
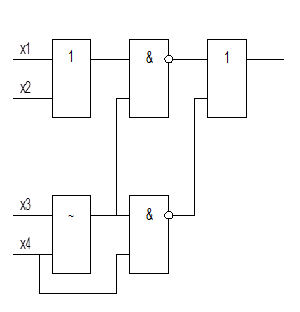
Виконати аналіз заданих на рис. 3.1. логічних схем, визначити відповідні логічні формули:
a b
c d
Рис. 3.1. Довільні логічні схеми
Виконати мінімізацію отриманих у задачі 3 логічних формул, синтезувати для мінімізованих формул нові логічні схеми.
 |  |
Виконати канонічний синтез логічних схем для формул задачі 1, оцінити їх за складністю способом, використаним раніше.
Побудувати логічні схеми і відповідні їм графи для МДНФ і МКНФ булєвих функцій (входи і виходи можна позначати як х01, х02, y01 і т.д.):
f(x1, x2, x3) = Ú(0, 2, 3, 4);
f(x1, x2, x3) = Ú(0, 2, 3, 4, 5, 7);
f(x1, x2, x3, x4) = Ú(1, 4, 5, 6, 12, 13, 14).
Мінімізація булевых функцій
Задачі
Виконати графічну мінімізацію заданих на рис.3.2. булєвих функцій від трьох перемінних, вважаючи виділені вершини конситуентами одиниці.
Виконати графічну мінімізацію заданих у задачі 2 булєвих функцій, вважаючи виділені вершини конституентами нуля.
Виконати графічну мінімізацію заданих за допомогою формул:
x1x2+ùx1ùx3+x2x3+ùx2ùx3;
(x1+x2)(ùx1+ùx2)(x2+ùx3);
(x1+ùx3)(x2+x4)(x1+ùx3+ùx4);
x1+ùx2+x3;
x1+ùx2+ùx3x4;
(ùx1+x2)(ùx2+x3);
ùx1ùx2ùx1+ùx2ùx3ùx4;
x1(x2+ùx4)ùx2(x1+ùx3);
 |  | ||
ùx2(x1+ùx2+x3+x4)ùx1ùx3(ùx2+x4)2x3(x1+x2)(ùx3+x4).
 |  |
a b
с d
Рис. 3.2. Графічне завдання булевых функцій
Виконати мінімізацію заданих булєвих функцій від трьох перемінних для ДНФ і КНФ за допомогою карт Карно:
a
Таблиця 3.2
| x1,x2 x3 | ||||
b
Таблиця 3.3
| x1,x2 x3 | ||||
c
Таблиця 3.4
| x1,x2 x3 | ||||
d
Таблиця 3.5
| x1,x2 x3 | ||||
Виконати мінімізацію булєвих функцій від чотирьох перемінних, для ДНФ і КНФ за допомогою карт Карно:
a
Таблиця 3.6
| x1,x2 x3x4 | ||||
b
Таблиця 3.7
| x1,x2 x3x4 | ||||
c
Таблиця 3.8
| x1,x2 x3x4 | ||||
d
Таблиця 3.9
| x1,x2 x3x4 | ||||
Виконати мінімізацію заданих чисельним методом булєвих функцій для ДНФ за допомогою методів Квайна-MакКласки і Петріка, застосувавши метод Петріка до скороченої таблиці покрить:
Ú(0, 2, 3, 6, 7, 10, 11, 12, 13, 15);
Ú(0, 2, 4, 5, 6, 8, 9, 10, 12, 14, 15);
Ú(2, 3, 5, 7, 8, 10, 11, 12, 13);
Ú(0, 2, 5, 7, 8, 10, 11, 13, 14, 15);
Ú(0, 2, 4, 5, 6, 7, 8, 9, 13).
Вирішити задачу 6 для КНФ тих же булєвих функцій, заданих чисельним методом, за допомогою методів Квайна-МакКласки і Петріка, застосувати метод Петріка до скороченої таблиці покрить:
Ù(1, 4, 5, 8, 9, 14);
Ù(1, 3, 7, 11, 13);
Ù(0, 1, 4, 6, 9, 14, 15);
Ù(1, 3, 4, 6, 9, 12);
Ù(1, 3, 10, 11, 12, 14, 15).
Застосувати метод Петріка до таблиць покрить задач 6, 7, обґрунтувати доцільність його використання для скорочених таблиць покрить.
Виконати мінімізацію заданих у задачі 6 булєвих функцій методом Блейка-Порецького для ДНФ.
Виконати мінімізацію заданих у задачі 7 булєвих функцій методом Блейка-Порецького для КНФ.
Порівняти ціни по Квайну МДНФ і МКНФ, отриманих у задачах 6 і 7 (чи 9 і 10, тому що результати повинні бути тотожні). Виконати аналітичне перетворення МДНФ у МКНФ і навпаки, переконавши в тотожності формул і правильності виконання мінімізації.
 |  |
Виконати графічну мінімізацію заданих на рис. 3.3. частково визначених булєвих функцій від трьох перемінних, вважаючи світлі виділені вершини відповідними конституентам одиниці, а темні виділені вершини – байдужним наборам.
a b
Рис. 3.3. Графічне завдання частково визначених булєвих функцій
Виконати графічну мінімізацію заданих на рис. 3.3. частково визначених булєвих функцій від трьох перемінних, вважаючи світлі виділені вершини відповідними конституентам нуля, а темні виділені вершини – байдужним наборам.
Виконати мінімізацію заданих часткових булєвих функцій від чотирьох перемінних за допомогою карт Карно:
a
Таблиця 3.10
| x1,x2 x3x4 | ||||
| х | х | |||
| Х | Х | |||
b
Таблиця 3.11
| x1,x2 x3x4 | ||||
| х | ||||
| Х | Х | |||
| Х | ||||
| Х |
Виконати мінімізацію заданих чисельним методом часткових булєвих функцій для ДНФ за допомогою методів Квайна-МакКласки і Петріка, застосувавши метод Петріка до скороченої таблиці покрить:
Ú(0, 2, 3, 6, 7, 10, 11, 12, 13), ´(8, 14, 15);
Ú(0, 2, 4, 5, 6, 8, 9, 10, 12, 14), ´(7, 11, 15);
Ú(2, 3, 5, 8, 10, 11, 12, 13), ´(1, 7, 9);
Ú(2, 5, 8, 10, 11, 14, 15), ´(0, 7, 13).
Вирішити задачу 15 для КНФ тих же часткових булєвих функцій, заданих чисельним методом, за допомогою методів Квайна-МакКласки і Петріка, застосувати метод Петріка до скороченої таблиці покрить:
Ù(1, 4, 5, 9), ´(8, 14, 15);
Ù(1, 3, 13), ´(7, 11, 15);
Ù(0, 4, 6, 14, 15), ´(1, 7, 9);
Ù(1, 3, 4, 6, 9, 12), ´(0, 7, 13).
Виконати мінімізацію заданих у задачі 15 часткових булєвих функцій методом Блейка-Порецького для ДНФ.
Виконати мінімізацію заданих у задачі 16 часткових булєвих функцій методом Блейка-Порецького для КНФ.
Порівняти ціни по Квайну для МДНФ і МКНФ, отриманих у задачах 15 і 16 (чи 17 і 18, тому що результати повинні бути тотожні). Виконати аналітичне перетворення МДНФ у МКНФ і навпаки, переконавши в необов'язковій тотожності формул, пояснити причину нетотожності.
Логіка предикатів
Задачі
На безлічі натуральних чисел визначені предикати P(x) = «число х поділяється на 8» і Q(x) = «х – парне число». Необхідно визначити наступні висловлення і з'ясувати які з них щирі:
"xP(x);
$xP(x);
"xQ(x);
$xù(Q(x));
"xù(Q(x));
"x(P(x)®Q(x));
"x(Q(x)®P(x));
$x(Q(x)®P(x)).
Нехай Х – безліч прямих на площині. На цій безлічі визначені предикати R(x, y) = «пряма х перетинається з прямой у», S(x, y) = «пряма х рівнобіжна прямої у», причому х,уÎХ. Необхідно визначити наступні висловлення і з'ясувати які з них щирі:
"x$yR(x, y);
$x$yù(S(x, y));
"x"y(R(x, y)®ù(S(x, y)));
"x"y(R(x, y)ÚS(x, y)).
На безлічі натуральних чисел визначені предикати P(x) = «число х - просте» і Q(x) = «х – парне число», R(x, y) = «х не дорівнює y». Необхідно перевести на розмовну мову формулу:
$x(P(x)ÙQ(x))Ù`$x(P(x)ÙQ(x)Ù$y(R(x, y)ÙP(y)ÙQ(y))).
Записати формули логіки предикатів для приведених тверджень:
«Кожен студент чи вивчає англійську мову, чи німецьку, чи французьку»;
«Деякі лабораторні стенди укомплектовані осцилографами»;
«Не всі комп'ютери працюють добре»;
«Жоден процесор не виявився забракованим»;
«Усі студенти, що виконали завдання, здали залік».
Граф G = (V, E) визначається завданням непорожньої безлічі вершин V, безлічі ребер Е і тримісного предиката P(x, e, y) = «ребро е з'єднує вершини х и у», що визначений на всіх упорядкованих трійках (x, e, y), причому х, уÎV і еÎЕ (для орграфа х вважається початкової вершиною дуги е, а y – кінцевою вершиною дуги е). Необхідно визначити предикати, що задають твердження:
«Підмножина дуг орграфа, що виходять з вершини а»;
«Підмножина дуг орграфа, що входять у вершину а»;
«Підмножина ребер графа, інцидентних вершині а»;
«Підмножина ребер графа, що з'єднує вершини а і b».
Відповідно до визначень графів із задачі 5 необхідно визначити висловлення для предикатів, показати, що для кожного е істинно одне і тільки одне з них, і назвати в термінології графів підмножини безлічі Е, що відповідають цим висловленням:
$x, y(x¹yÙP(x, e, y)Ùù(P(y, e, x)));
$x(P(x, e, x));
$x, y(x¹yÙP(x, e, y)Ù(P(y, e, x))).
ГРАФИ






