Вступ
Методичні вказівки і завдання до контрольних робіт використовуються при вивченні дисципліни «Основи дискретної математики» студентами очної та заочної форм навчання і включають задачі з п'яти основних розділів «Елементи теорії множин», «Комбінаторика», «Булєва алгебра», «Графи» і «Кінцеві автомати».
При використанні студентами очної форми навчання методичні вказівки і завдання можуть бути збірником задач до практичних занять та домашньої роботи. Вибір матеріалу для занять виконується викладачем відповідно робочої програмі дисципліни.
При використанні студентами заочної форми навчання методичні вказівки і завдання дають практичний матеріал для двох контрольних робіт. У цьому випадку перша контрольна робота містить задачі розділів «Елементи теорії множин», «Комбінаторика» і «Графи», друга контрольна робота містить задачі розділів «Булєва алгебра» і «Кінцеві автомати».
Варіант контрольних робіт вибирається на підставі унікального індексу студента і індексу задачі.
Індивідуальний індекс студента вибирається на підставі останніх трьох цифр номера залікової книжки студента, наприклад, при останніх трьох цифрах номера залікової книжки «102» буде дорівнювати «Iстудента=102», при останніх трьох цифрах номера залікової книжки «054» – «Iстудента=54», при останніх трьох цифрах номера залікової книжки «007» – «Iстудента=7».
Більшість задач методичних рекомендацій задано в декількох варіантах, наприклад, задача 1 розд. 1.1. задана в п'ятьох варіантах (a, b, c, d, e). Отже, індекс (число варіантів) цієї задачі дорівнює п'яти «Iзадачі=5».
Кожен студент повинний вирішити всі одноваріантні задачі і тільки один індивідуальний варіант у різноманітних задачах. Індивідуальний варіант різноманітної задачі «Варіант(Iстудента, Iзадачи)» утвориться як залишок від розподілу унікального індексу студента на індекс (число варіантів) цієї задачі, збільшений на одиницю.
Приклад
«Вар. (Iстудента=13, Iзадачи=5) = (13/5)+1 = 4»;
«Вар. (Iстудента=142, Iзадачи=5) = (142/5)+1 = 3»;
«Вар. (Iстудента=002, Iзадачи=7) = (2/7)+1 = 3».
Число задач контрольних робіт складає 270. Студенту необхідно правильно вирішити: для відмінної оцінки – не менш 250 задач; для гарної оцінки – не менш 200 задач, для задовільної оцінки – не менш 150 задач.
ТЕОРІЯ МНОЖИН
Основи теорії множин
Задачі
Які з приведених співвідношень вірні, які ні? Чому?
a) х Î ({2, a, x };
b) 3 Î {1, {2, 3}, 4};
c) х Î {1, sin X };
d) {x, y} Î {a, {x, y}, b};
e) {1,2} Î {{1, 2, 3}, {1, 2}, 1, 2}.
Чи рівні між собою безлічі А и В (якщо ні, то чому)?
a) A = {2, 5, 4}; B = {5, 4, 2};
b) A = {1, 2, 4, 2}; B = {1, 2, 4};
c) A = {2, 4, 5 }; B = {2, 4, 3};
d) A = {1, { 2, 5}, 6}; B = {1, {5, 2}, 6};
e) A = {1, {2, 5}, 6}; B = {1, 2, 5, 6}.
Чи вірно, що для довільної безлічі A Î A?
Чи зв'язані безлічі А и В відношенням включення, якщо так, то вкажіть, яка з них є підмножиною іншої?
a) A = {a, b, d}; B = {a, b, c, d};
b) A = {a, b, c, d, e}; B = {a, e, c};
c) A = {c, d, e}; B = {a, c};
d) A = {a, {b, c}, d, e}; B = {a, b, c, d};
e) A = {{a, b, c, d}}; B = {a, b, c, d}.
Перелічити всі елементи безлічі P(A) (тобто всі підмножини безлічі А):
a) A = {1, 2, 3};
b) A = {1, 2, {1, 2}};
c) A = {{1, 2}, {3}, 1}.
Довести наступні твердження для довільних безлічей A, B, C:
A Í A (рефлексивність);
якщо A Í B і В Í С, то А Í С (транзитивність);
якщо А Í В и В Í С, то А Í С;
якщо А Í В и В Í С, то А Í С;
якщо А Í В и В Í З, то А Í С.
Які з тверджень вірні для всіх безлічей A, B, C, чому?
a) якщо A Î B і В Î С, то А Î С;
a) якщо А Î В и В Î С, то А Î С;
b) якщо A Î B і В Î С, то А Î С;
c) якщо А Í В и В Ï С, то А Î С;
d) якщо A Ï B і В Ï С, то А Ï С.
Довести, що для будь-яких безлічей А1, A2,...., An, якщо А1 Í A2 Í..... Í An Í A1 , то A1 = А2 =... = An.
Знайти А È В, A Ç B, A\B, B\A, якщо:
A = [3,5], B = [2,4];
A = [3,5], B = (2,4);
A = (3,5), B = [2,4];
A = (3,5), B = (2,4).
тут прийнято: [a,b] = M {x Î D | a <= x <= b}; (a,b) = M {x Î D | a < x < b};
Знайти А È B, A Ç B, A\B, B\A, якщо:
А = {x Î А | х Î N і x поділяється на 4 і х <= 40},
B = {x Î B | х Î N і x поділяється на 5 і х <= 40};
А = {x Î А | х Î N і x поділяється на 4 і х <= 30},
B = {x Î B | х Î N і x поділяється на 6 і х <= 40}.
Довести тотожності (властивості) 1 - 18.
Довести чи спростувати наступні твердження:
якщо АÇВ Í `С і АÈС Í В, то АÇС = Æ.
якщо А Í ù(ВÈC) і B Í ù(AÈC), то B = Æ.
(A\B)ÈC = (AÈC)\(BÈC).
(A\B)\C = (A\C)\B.
(AÈB)\(AÇB) = (AÇ`B)È(BÇ`A).
Знайти необхідні і достатні умови для виконання рівностей:
(A\B) ÈB = A;
(AÈB) \B = A;
A\B = A;
(AÈB)\(AÇB) = Æ.
Довести наступні тотожності:
(AÈB)Ç(CÈD)=(AÇC)È(AÇD)È(BÇC)È(BÇD);
AÇ(BÈCÈD)=(AÇB)È(AÇC)È(AÇD);
AÈ(B\A) = AÈB;
(AÈB)\(AÇB)=(A\B)È(B\A);
(AÈB)\(AÇB)=(AÇB)È(BÇA);
A\B = AÈ(AÇB);
(C\A)Ç(C\B) = AÈBÈC;
A\(B\C) = (A\B)È(AÇC);
A\(BÈC) = (A\B)\C.
Що можна сказати про співвідношення безлічей А и В, якщо:
AÈC Í BÈC;
AÇC Í BÇC;
(A\C) Í (B\C);
(C\B) Í (C\A);
ùB Í ùA;
AÇB = AÈB;
(A\B)È(B\A) = Æ.
Побудувати двоїсті вираження для вихідних виражень:
AÈC Í BÈC;
AÇC Í BÇC;
(A\C) Í (B\C);
(C-B) Ì (C-A);
ùB Í ùA;
AB = AÈB;
(A\B)È(B\A) = Æ.
Довести тотожності:
A-B = B-A;
A-(B-C) = (A-B)-C;
AÇ(B-C) = (AÇB)-(AÇC);
A-(A-B) =B;
A-B-(AÇB) = AÈB;
A-(AÇB) = A\B;
(A-B)È(AÇB) = AÈB.
Нехай Х = (А\B)\C; Y =A\(B\C). Чому дорівнює Y\X? Як співвідносяться Х и Y?
Спростити вираження:
(AÇBÇD)È(AÇBÇCÇDÇE)È(AÇDÇ`A);
(AÇBÇC)È(`AÇBÇC)È`BÈ`C;
(AÇBÇCÇ`D)È(`AÇC)È(`BÇC)È(CÇD);
ù((AÈ(AÇB))Ç(BÈ(AÇB))ÇC);
((AÇC)\(BÇC))È((BÇC)Ç(`AÈ`BÈ`C)).
Вирішити рівняння:
АÇ`Х = ВÇ(ХÈ`С);
ù(АÈХ)È`С = ВÈХÇС;
(АÈВÈ`С)ÇХ = ù(ВÇХ);
(А-(ВÇ`Х))ÇС = ù(ВÈ`С).
Знайти покриття для вихідних безлічей, блоки яких містять по чотири, три і два елементи, знайти одну можливу розбивку і тривіальні розбивки:
{a, b, c, d, e, f, g};
{1, 3, d, 7, h, r, v};
{b, d, 6, h, k, x, 9};
{I, III, A, VII, F, L, XIV, Z}.
Показати еквівалентність:
безлічі натуральних чисел N і безлічі квадратів натуральних чисел N2;
безлічі цілих чисел С и безлічі парних чисел;
безлічі дійсних чисел D і безлічі всіх точок прямої;
безлічі точок осі абсцис і безлічі точок одиничного нижнього півкола з центром у точці (0, 1) за винятком її кінців (-1, 1) і (1, 1);
безлічі точок інтервалу (0;1) і безлічі всіх дійсних чисел D.
Упорядковані множини
Задачі
Задано безлічі А={1, 2}; B={3, 4}; C={4, 5, 6}.Знайти:
A´B;
B´A;
(A´B)´C;
A´(B´C);
A´B´C;
C´(B´A);
C´B)´A.
Задано безліч А={a, b}. Знайти A0, A1, A2, A3.
Знайти геометричну інтерпретацію наступних безлічей:
[a, b]´[c, d], де [a, b] і [c, d] - відрізки дійсної прямої;
[a, b]2;
[a, b]3.
Довести чи спростувати:
As´At = As + t, A ¹ Æ;
As´At = At´As, A ¹ Æ;
A Í Ms, B Í Mt, A ¹ Æ, B ¹ Æ, A´B Í Ms + t
Довести, що:
(AÇB)´(CÇD) = (A´C)Ç(B´D);
(A´B)È(C´D) Í (AÈC)´(BÈD)
При яких A, B, C, D виходить рівність?
(AÈB)´C = (A´C)È(B´C);
A´(BÈC) = (A´B)È(A´C);
(AÈB)´(CÈD) = (A´C)È(B´C)È(A´D)È(B´D);
(A\B)´C = (A´C)\(B´C);
A´(B\C) = (A´B)\(A´C);
A´B = (A´D)Ç(C´B), де A Í C, B Í D.
Чи дистрибутивне пряме множення безлічей щодо операцій перетинання й об'єднання? Чи дистрибутивні об'єднання і перетинання щодо прямого множення? Відповідь обґрунтувати.
Визначити проекції векторів пр1,4(abbacebf), пр2,4,7<11010001000> і пр3,4,2,8(75d442mk009).
Довести чи спростувати, що
пр1(А´B) = А;
пр2 (A´У) = B;
якщо С Í A´В, то пр1 C Í A; пр2 C Í В.
Знайти інверсії векторів (abbacebf)-1, <11010001000>-1 і (75d442mk009)-1.
Задано вихідні безлічі А={1, 2}; B={3, 4}; C={4, 5, 6}.Знайти інверсії:
(A´B)-1;
(B´A)-1;
((A´B)´C)-1;
(A´(B´C))-1;
(A´B´C)-1;
(C´(B´A))-1;
(C´B)´A)-1.
Нехай [a, b] і [c, d] - відрізки дійсної прямої, знайти інверсії:
([a, b]´[c, d])-1;
([a, b]2)-1;
([a, b]3)-1;
([a, b]2)-1´[c, d]-1.
Графіки
Задачі
Нехай [a, b], [a, b), (a, b] відповідно відрізок і напіввідрізки, (a, b) – координати точки на площині. Побудувати графіки на площині, знайти області визначення і значення (перші і другі проекції) графіків:
([2, 4]´[-1, 1))Ç([1, 3)´(-2, 0]);
((3, 5)´[-2, 0])-([2, 4]´[-1, 1));
G = {(1, 2), (-2, 4), (2, 7), [1, 2]´[-1, 1)};
G = {(x, y)ÎG| (0<x<1 і y = 2) чи (x>2 і 1<y<3)};
G = {(x, y)ÎG| y = 2x-4 і 1<x<5};
G = {(x, y)ÏG| y = 3x+3 і x<7}.
Для графіків задачі 1 визначити інверсії, знайти області визначення і значення:
(([2, 4]´[-1, 1))Ç([1, 3)´(-2, 0]))-1;
(((3, 5)´[-1, 0])È([2, 3]´[-1, 2)))-1;
G = {(1, 2), (-2, 4), (2, 7), [1, 2]´[-1, 1)}, знайти G-1;
G = {(x, y)ÎG| (0<x<1 і y = 2) чи (x>2 і 1<y<3)}, знайти G-1;
G = {(x, y)ÎG| y = 2x-4 і 1<x<5}, знайти G-1.
Для графіків G1, G2 і G3 побудувати декартові добутки G = G1´G2 і G = G1´G2´G3, знайти області визначення і значення:
G1 = {(1, 5), (-4, 4), (3, 9)}, G2 = {(2, 5), (2, 9), (3, 11), (7, 10)};
G1 = {(1, 2), (2, 3), (2, 5), (4, 3)}, G2 = {(1, 1), (2, 4), (2, 10), (3, 10), (5, 11)}, G3 = {1, -11), (2, 4), (4, 6), (4, 8), (11, 9)};
G1 = [2, 3]´[-1, 2), G2 = [0, 2)´(-1, 0];
G1 = {(x, y)ÎG1| (0<x<1 і y = 1) чи (x>-1 і 2<y<3)}, G2 = {(x, y)ÎG2| (1<x<2 і 3<y<4)};
G1 = {(x, y)ÎG| y = x+7 і -1<x<1}, G2 = {(x, y)ÎG2| (y ³ x2)}.
Для графіків G1, G2 і G3 побудувати композиції G = G1°G2 і G = G1°G2°G3, знайти області визначення і значення:
G1 = {(1, 2), (-2, 4), (2, 7)}, G2 = {(1, 5), (2, 9), (2, 11), (7, 11)};
G1 = {(1, 2), (2, 3), (2, 5), (4, 3)}, G2 = {(1, 1), (2, 4), (2, 10), (3, 10), (5, 11)}, G3 = {1, -11), (2, 4), (4, 6), (4, 8), (11, 9)};
G1 = [2, 4]´[-1, 1), G2 = [0, 3)´(-2, 0];
G1 = {(x, y)ÎG1| (0<x<2 і y = 1) чи (x>-1 і 2<y<5)}, G2 = {(x, y)ÎG2| (0<x<1 і 0<y<3)};
G1 = {(x, y)ÎG| y = 2x+4 і -1<x<5}, G2 = {(x, y)ÎG2| (y ³ 0,5x2-3)}.
Для результуючих композицій задачі 4 побудувати інверсії.
Довести, що операція композиції графіків не комутативна й асоціативна.
Визначити властивості графіків (симетричність, функціональність, ін’єктивність):
G = {(1, 2), (2, 3), (2, 5), (4, 4)};
G = {(1, 2), (2, 1), (4, 5), (5, 4), (3, 3)};
G = {([2, 4]´[-1, 1))Ç([-1, 1)´[2, 4])};
G = {(x, y)ÎG| (0<x<2 і y ³ 1) чи (x>-1 і 2<y<5)};
G = {(x, y)ÎG| y = -3x+14};
G = {(x, y)ÎG2| (y = 0,5x2-2)}.
Відповідності, образи і прообрази
Задачі
Для відповідностей g1 і g2 знайти об'єднання, перетинання, різниці, симетричну різницю і доповнення:
g1 = ({1, 2, 3, 4, 5}, {a, b, c, d, e, f}, {(1, a), (2, b), (3, c), (4, f)}), g2 = ({1, 3, 5, 6, 7}, {a, c, e, f, g}, {(1, a), (2, b), (3, c), (4, f)}, (7, e));
g1 = (N, N, {(2, 5), (3, 3), (3, 4), (6, 9)]}), g2 = (N, N, {(1, 1), (2, 5), (3, 4), (6, 8)});
g1 = (N, N, {[2, 5]´[1, 2)}), g2 = (C, N, {[-1, 1)´[2, 3]});
g1 = (C, C, {(x, y)ÎG| (1<x<2 і y ³ 1)}), g2 = (C, C, {(x, y)ÎG| x>-1 і 2<y<4)});
g1 = (D, D, {(x, y)ÎG| y £ -3x+14}), g2 = (D, D, {(x, y)ÎG2| (y ³ x2+1)}).
Для відповідностей g побудувати інверсії і звуження на безліч А:
(= ({1, 2, 3, 4, 5}, {a, b, c, d, e, f}, {(1, a), (3, b), (4, c), (5, f)}), А = {2, 3, 4};
(= (N, N, {(1, 1), (2, 5), (3, 2), (6, 7)}), A = {[0, 3]};
(= (C, N, {[-2, 4)´[3, 5]}), A = {[-2, 0]};
(= (C, C, {(x, y)ÎG| (1<x<6 і y (2)}), A = {[-1, 3]};
g = (C, C, {(x, y)ÎG| x>-4 і 1<y<7)}), A = {[3, 5)};
g = (D, D, {(x, y)ÎG| y £ -2x+10}), A = {[-1, 3]};
g = (D, D, {(x, y)ÎG2| (y ³ x2+4)}), A = {[3, ¥)}.
Для відповідностей g1, g2 і g3 побудувати декартові добутки g = g1´g2 і g = g1´(g2´g3):
g1 = ([-5, 5], [1, 10], {(1, 5), (-4, 4), (3, 9)}), g2 = ([2, 7], [5, 12], {(2, 5), (2, 9), (3, 11), (7, 8)});
g1 = (N, N, {(1, 2), (2, 3), (2, 5), (4, 3)}), g2 = (N, N, {(1, 1), (2, 4), (2, 10), (3, 10), (5, 11)}), g3 = (N, N, {1, -11), (2, 4), (4, 6), (4, 8), (11, 9)});
g1 = (C, N, {[2, 3]´[-1, 2)}), g2 = (C, C, {[0, 2)´(-1, 0]});
g1 = (C, N, {(x, y)ÎG1| (1<x<2 і y = 4) чи (x>-1 і 1<y<3)}), g2 = (N, N, {(x, y)ÎG2| (3<x<4 і 5<y<7});
g1 = (D, D, {(x, y)ÎG| y = x+7 і -1<x<1}), g2 = (D, D, {(x, y)ÎG2| (y ³ x2)}).
Для відповідностей g1, g2 і g3 побудувати композиції g = g1°g2 і g = g1°g2°g3 і їхні інверсії:
g1 = ([-5, 5], [1, 10], {(1, 5), (-4, 4), (3, 9)}), g2 = ([2, 7], [5, 12], {(3, 5), (4, 9), (5, 11), (5, 8)});
g1 = (N, N, {(1, 2), (2, 3), (2, 5), (4, 3)}), g2 = (N, N, {(1, 1), (2, 4), (2, 10), (3, 10), (5, 11)}), g3 = (N, N, {1, -11), (4, 4), (4, 6), (10, 8), (11, 9)});
g1 = (C, N, {[2, 3]´[-1, 2)}), g2 = (C, C, {[0, 2)´(-1, 0]});
g1 = (C, N, {(x, y)ÎG1| (1<x<2 і y = 4) чи (x>-1 і 1<y<3)}), g2 = (N, N, {(x, y)ÎG2| (0<x<4 і 5<y<7});
g1 = (D, D, {(x, y)ÎG| y £ x+7 і -1<x<1}), g2 = (D, D, {(x, y)ÎG2| (y ³ x2)}).
На безлічі А = {1, 2, 3, 4, 5} задані відповідності. Визначити їхні області відправлення, визначення прибуття і значень, а також властивості відповідностей, якщо графіки мають вид:
{(1, 2), (2, 3), (2, 4), (3, 2), (5, 1)};
{(2, 1), (3, 4), (4, 4), (5, 3)};
{(1, 2), (2, 3), (3, 2), (4, 3), (5, 1)};
{(1, 2), (2, 3), (4, 1), (4, 1), (4, 5), (5, 5)};
{(1, 5), (2, 1), (3, 4), (4, 3), (5, 2)}.
Знайти області відправлення, визначення, прибуття і значень відповідностей, побудувати їхні графіки на площині і визначити властивості відповідностей, якщо їхні графіки мають вигляд:
{(x, y) Î D2| y = x};
{(x, y) Î D2| y>=x};
{(x, y) Î D2| 0<=x<=2 чи 0<=y<=1};
{(x, y) Î D2| 0<=x<=2 чи 0<=y<=1};
{(x, y) Î D2| x2 + 4y2 =1};
{(x, y) Î D2| x2 = y2 };
{(x, y) Î D2| |x| +2 |y|=1};
{(x, y) Î D2| x2 + y2 < 1 і x > 0};
{(x, y) Î D2| y >= 0 і y <= x, і x + y <=1}.
Які з приведених відповідностей, заданих на безлічі дійсних чисел D, є функціональними? Визначити всі їхні області й всі інші властивості:
{(x, y) Î D2| y = x2 + 2x +1};
{(x, y) Î D2| x = y2 };
{(x, y) Î D2| |x| +|y| =1};
{(x, y) Î D2| x2 + y2 =1 і y > 0}.
Які з відповідностей, задані графіками на рис.1.1, є функціями? Які з них взаємооднозначні? Визначити їхні всі області і властивості.
1 a y y
2 b
3 c
x
4 d x
 |
5 e
f
a b c
y y
x x
 |  |
d e
Рис.1.1.
Довести справедливість наступних тверджень (лему):
g – функція Û g-1 – ін'єкція;
g – усюди визначено Û g-1 – сюр'єкція;
g – бієкція Û g-1 – бієкція.
Нехай A= {a, b, c, d, e, f}; g= (A, A, P), A’= {a, b, d, f}, P= {(a, e), (c, b), (d, d), (e, c), (f, b), (a, d)}. Знайти образ g(A’) і повний прообраз g-1(A’).
Нехай g - відповідність між D і D з графіком Р={(x, y) Î D2| y-3x+2=0} Знайти образ g(А) і повний прообраз g-1(A), якщо:
A=[2, 3];
A=[-2, 3];
A=[-1, 1].
Вирішити задачу 11, якщо Р={(x, y) Î D2| y= x2-1}.
Вирішити задачу 11, якщо Р={(x, y) Î D2| y= -3x3+2}.
Довести чи спростувати, що для образів будь-якої відповідності g = (A, B, P) і будь-яких безлічей А' і A” виконується:
g(A’ÈA”) = g(A’)Èg(A”);
g(A’ÇA”) = g(A’)Çg(A”);
g(A’\A”) = g(A’)\g(A”).
Знайти необхідні і достатні умови, які повинні задовольняти відповідність g, щоб для образів відповідності для безлічей А' і A” виконувалися тотожності:
g(A’ÇA”) = g(A’)Çg(A”);
g(A’\A”) = g(A’)\g(A”).
Довести, що для образів відповідності g = (A, B, P) і безлічей A’, A”, B’ справедливі:
A’ Í A” Þ g(A’) Í g(A”);
g(A’) = g(A’Çпр1P);
g-1(B’) = Æ Û B’Çпр2P = Æ.
Довести справедливість тверджень для відображення g = (A, B, P):
g(A’ÈA”) = g(A’)Èg(A”);
g(A’ÇA”) Í g(A’)Çg(A”);
g-1(B’ÈB”) = g-1(B’)Èg-1(B”);
g-1(B’ÇB”) = g-1(B’)Çg-1(B”).
Визначити характеристичні функції для безлічей А і підмножин А':
A = {1, 2, 3, 4, 5, 6}, А' = {2, 4, 5};
A = {(-2, 5]}, A’ = {[-1, 0]È(1, 3]};
A = {xÎA| xÎN і x<8}, A’ = {xÎA’| xÎN і х<5 і x – парне}.
Побудувати діаграми для відображень g1, g2, g3, g4, g5, чи комутативні побудовані діаграми?
g1 = ({1, 2, 3, 4}, {1, 2, 3, 4, 5}, (1, 2), (2, 3), (3, 5), (4, 3)}), g2 = ({2, 3, 4, 5}, {3, 4, 5, 6, 7}, {(2, 7), (3, 4), (4, 6), (5, 5)}), g3 = ({1, 2, 3, 4}, {3, 4, 5, 6, 7}, {(1, 7), (2, 4), (3, 5), (4, 4)});
g1 = (D, D, {(x, y)ÎG| y = 2x}), g2 = (D, D, {(x, y)ÎG| y = |x|}), g3 = (D, D, {(x, y)ÎG| y = |x|}), g4 = (D, D, {(x, y)ÎG| y = 2x});
g1 = ({[-3, 5]}, D, {(x, y)ÎG| y = 3x-5}), g2 = (D, N, {(x, y)ÎG| -2<x<6 і y = |mod(x, 2)|}), g3 = ([-3, 5], D, {(x, y)ÎG| y = 6x}), g4 = (D, C, {(x, y)ÎG| y = mod((0,5x-5), 2)}), g5 = (C, N, {(x, y)ÎG| y = |x|}).
Відношення. Функції
Задачі
На безлічах А = {a1, a2, a3, a4, a5,} і В ={b1, b2, b3, b4,} визначено бінарне відношення R={(a1, b2), (a2, b1), (a2, b2), (a4, b2), (a4, b3), (a5, b1), (a5, b3)}:
визначити область визначення й область значень відношення;
визначити перетини по кожному елементі з А;
визначити перетини по підмножинах А1 = {a1, a4,} і А11 ={a2, a3, a5,};
побудувати матрицю і граф відношення;
знайти зворотне відношення R-1.
Визначити за допомогою характеристичної властивості графіки тернарних відношень, що задають бінарні арифметичні операції додавання, вирахування, множення, розподілу на безлічі цілих чисел.
Визначити за допомогою характеристичної властивості графіки тернарних відношень, що задають оператори мови Java (C) на безлічі дійсних чисел:
if(a<(b*c)) a+=2*b; else a/=2*c;
for(i=0; i<10; i++) a=i+2*b;
a=(a>b? a+3: a-2).
Визначити за допомогою характеристичної властивості графіки п’ятиарних відношень, що задає оператор case мови Java (C):
switch(i): {
case 1: a=b; break;
case 2: b+=7*c; break;
case 3: b*=a;
case 4: b/=2-d; break;
default: a=0; b=0; }
За допомогою матриці задайте будь-яке шестиарне відношення на безлічі букв латинського алфавіту.
Нехай задані два відношення:
R1 = {(x, y)ÎR1| x, y – безліч одеситів і х є батьком у},
R2 = {(x, y)ÎR2| x, y – безліч одеситів і х є дочкою y}.
Побудувати бінарні відношення:
(R1)2 і (R2)2;
((R1)-1)°R2 і R2°(R2)-1;
((R1)-1)°(R2)-1 і ((R2)-1)°(R2)-1.
Для відношень R1, R2, R3, заданих за допомогою матриць,
R1 = 1, 3, 1, 1, 4 R2 = 2, 4, 4, 2, 3 R3 = 4, 4, 2
2, 4, 2, 2, 3 4, 9, 4, 4, 1 3, 3, 2
4, 1, 3, 2, 7 3, 2, 3, 5, 2 2, 3, 4
4, 9, 4, 4, 1 3, 2, 2, 5, 2 3, 3, 4
і безлічі A = {a, b, c} визначити (у матричній формі):
об'єднання, перетинання, дві різниці, симетричну різницю відношень R1, R2, а також доповнення відношення R3 у припущенні, що R3 діє на безлічі B = {2, 3, 4};
декартові добутки R1´R2, R1´R3, R2´R1;
перестановки координат відношень R1, R2 відповідно до набору (3, 2, 4, 1, 5), відношення R3 відповідно до вектора (1, 3, 2);
цикли, транспозиції і зворотні відношення для вихідних відношень R1, R2, R3;
ототожнення координат для відношень R1, R2, R3 відповідно до векторів координат (1, 3, 4) для R1, (2, 3) для R2, (1, 2) для R3;
приписування фіктивної координати з безлічі А для відношень R1, R2, R3;
згортки де Моргана для відношень R1, R3;
проекції відношень пр1,3,5R1, пр2,4R2, пр3R3 і доповнень проекцій відношень ù(пр1,3,5R1), ù(пр2,4R2), ù(пр3R3);
перетинів відношень R1, R2, R3 відповідно по векторах (41, 12, 33, 24), (31, 22, 54, 25), (32, 43);
перетину відношення R3 по безлічі векторів {(31, 32), (32, 43)};
присутність властивостей усюди визначеності, функціональності, ін’єктивності, сюр’ективності і бієктивності для відносин R1, R2, R3 за умови їхнього відображення в бінарні відносини відповідно до угруповання координат (1, 2, 3, 4, 5)Þ((1, 2, 3, 4), (5)) для R1, (1, 2, 3, 4, 5)Þ((1, 2), (3, 4, 5)) для R2, (1, 2, 3)Þ((1), (2, 3)) для R3.
Задати унарне відношення на безлічі A = {a, b, c, d, e, f, g, h} за допомогою характеристичної властивості підмножини А':
A’ = {a, d, e, h};
A’ = {b, c, f};
A’ = {a, b, c, g};
A’ = {c, d, f, g}.
Для відношень R1, R2, R3, R4, R5 S на безлічі З, заданих за допомогою матриць, визначити:
R1 = 1, 3, 1, 1, 4 R2 = 2, 4, 4, 2, 3 R3 = 4, 1, 3, 2, 4
2, 4, 2, 2, 3 1, 3, 1, 1, 7 1, 3, 1, 1, 5
4, 1, 3, 2, 7 3, 2, 3, 5, 2 2, 3, 4, 3, 2
4, 9, 4, 4, 1 1, 3, 1, 1, 2 3, 3, 4, 1, 5
4, 1, 3, 2, 5
R4 = 1, 3, 1, 1, 2 R5 = 1, 3, 1, 1, 3 S = 1, 1, 2, 4, 3, 6
6, 8, 5, 5, 2 3, 2, 1, 4, 4 4, 2, 5, 2, 4, 8
4, 1, 3, 2, 1 4, 1, 3, 2, 9 7, 5, 4, 1, 9, 7
1, 3, 1, 1, 4 2, 4, 3, 1, 6, 7
4, 2, 5, 2, 3, 9
4, 7, 5, 2, 3, 5
7, 5, 4, 1, 9, 8
суперпозицію S(R1, R2, R3, R4, R5) у матричній формі;
наявність функціональності в суперпозиції.
Для чотир’охарних відношень на безлічі A = {a, b, c} визначити присутність властивостей рефлексивности, симетричності, транзитивності і зв'язності без умови відображення їх у бінарні відношення і з умовою відображення їх у бінарні відношення відповідно до угруповання координат (1, 2, 3, 4, 5)Þ((1, 2), (3, 4)):
R = {(a, a, c, b), (c, a, b, b), (b, c, c, a), (a, b, c, c), (b, a, a, c), (a, a, a, a)};
A = {(a, b, c, a), (b, a, c, b), (b, c, a, a), (a, c, b, c), (c, a, c, b), (c, c, c, c)};
A = {(a, a, a, a), (b, b, b, b), (c, c, c, c), (a, b, a, b), (c, a, a, c), (a, c, c, a)};
A = {(a, b, c, a), (a, a, b, c), (a, c, b, a), (a, b, a, c), (a, a, c, b), (a, c, b, a),
(b, a, a, c), (b, a, c,a), (b, c, a, a), (c, a, a, b), (c, a, b, a), (c, b, a, a)}.
Чи існують такі безлічі А и В, для бінарних відношень яких справедливо R-1АВ = ` RАВ?
Приведіть приклади рефлексивних, антирефлексивних, іррефлексивних, симетричних, антисиметричних, асиметричних, транзитивних, нетранзитивних, зв'язних і незв'язних бінарних відношень.
Побудувати бінарні відношення:
рефлексивне, симетричне, нетранзитивне;
рефлексивне, антисиметричне, нетранзитивне;
рефлексивне, транзитивне, несиметричне;
антисиметричне, транзитивне, іррефлексивне;
асиметричне, транзитивне, іррефлексивне.
Визначити властивості наступних бінарних відношень на довільній безлічі А:
повного відношення (А,A2);
порожнього відношення (А, Æ);
відношення рівності (A, EA);
відношення нерівності (A, `EA).
Побудувати графіки і визначити властивості наступних бінарних відношень:
a R b º |a-b|£1, де a, b Î D;
a R b º a£b£a2, де a, b Î C;
a R b º a£3b£a3, де a, b Î D;
a R b º a £ b, де a, b Î D;
a R b º a = b = 0, де a, b Î D;
a R b º x, y > 0, де a, b Î D;
r = ({1, 2, 3}, R), R={(1, 1), (1, 2), (2, 2)};
r = (Æ, Æ);
a R b º |a-b|£3, де a, b Î D;
a R b º [a - b =7t], де a, b, t Î N;
r = (A, R), де А ={a, b, c, d,}; R={(a, a),(a, b),(c, a),(b, d),(a, d),(b, c)}.
Спеціальні види відношень
Задачі
Нехай А - безліч усіх прямих на площині. Чи є еквівалентністю наступні відношення:
паралельність прямих;
перпендикулярність прямих.
Відношення еквівалентності на безлічі А ={1, 2, 3, 4, 5, 6, 7} задано розбивкою на класи А1 = {1, 4}; A2 = {2, 3, 7}; A3 = {5, 6}. Представити це відношення безліччю упорядкованих пар, матрицею і графом.
Показати, що кожне з наступних відношень є відношенням еквівалентності:
повне відношення на довільній безлічі А;
відношення рівності на довільній безлічі А;
відношення “бути в одній групі” на безлічі студентів факультету;
відношення “мати однаковий залишок при розподілі на 3” на безлічі N;
відношення подоби на безлічі трикутників;
відношення концентричності на безлічі окружністів;
відношення мати однакове число цифр на безлічі N;
відношення мати однакову обчислювальну потужність.
Нехай f: x ® y - відображення. На безлічі Х задане відношення R таке, що х1Rх2, якщо f(х1) = f(х2). Чи є R відношенням еквівалентності?
Показати, що наступні відношення не є еквівалентністю:
відношення нерівності на безлічі А (А ¹ Æ);
відношення “ а кратне b ” на безлічі цілих чисел З;
відношення “ а знайомий з b “ на безлічі людей;
порожнє відношення.
Нехай А и В - відношення еквівалентності. Чи є еквівалентністю відношення:
AÈB;
AÇB;
A\B;
A-B;
ùA.
Визначити властивості і вказати тип упорядкованості для наступних відношень:
відношення <= (не більше) на безлічі дійсних чисел D;
відношення < (менше) на безлічах D, R, C, N;
відношення Í (включення) на безлічі підмножин безлічі А;
відношення Ì (строге включення) на безлічі підмножин безлічі А;
відношення “бути дільником” на безлічі натуральних чисел;
відношення “бути старше” на безлічі людей;
відношення “бути довше” на безлічі відрізків на площині.
Визначити властивості і вказати тип упорядкованості для наступних відносин, заданих на безлічі А ={a, b, c, d}
r1=(A, R1), R1={(a, b), (a, d), (b, d), (a, c)};
r2=(A, R2), R2={(a, b), (a, c), (a, d)};
r3=(A, R3), R3={(a, b)};
r4=(A, R4), R4={(a, c), (a, d), (b, c), (b, d)};
r5=(A, R5), R5={(a, a), (a, c), (a, d), (b, b), (b, c), (b, d), (c, c), (c, d), (d, d)}.
До якого типу упорядкованості відносяться наступні відношення:
будь-яке відношення еквівалентності на довільній безлічі А;
відношення b поділяється на a (a, b Î C);
відношення a не старше, ніж b на безлічі людей Землі;
відношення a не старше курсом, ніж b на безлічі студентів факультету;
відношення рівності ЕА.
Замикання відношень. Замкнутість щодо операцій
Задачі
Побудувати транзитивне і рефлексивне замикання для бінарних відношень:
R1 = {(x, y)ÎR1| x, yÎN і y = x+1};
R2 = {(x, y)ÎR2| x, yÎD і y>x};
R3 = {(x, y)ÎR3| x, yÎD і |x| = |y|}
R4 = {(x, y)ÎR4| x, yÎD і x*y = 1};
R5 = {(x, y)ÎR5| x, yÎD і |x|+|y| = 1}.
Побудувати транзитивне і рефлексивне замикання для бінарних відношень:
R4 = {(x, y)ÎR4| x, y – станції Одеського метрополітену і y є наступною станцією за х};
R5 = {(x, y)ÎR5| x, y – безліч одеситів і х є батьком у};
R6 = {(x, y)ÎR6| x, y – безліч одеситів і х є дочкою в};
R7 = {(x, y)ÎR7| x, y – безліч одеситів і х є знайомим у}.
Побудувати транзитивне і рефлексивне замикання для бінарних відношень:
(R6°(R6-1))+;
((R5-1)°R5)*;
((R6)-1°(R5)-1)+;
(R6°(R6-1)°R6)+;
((R6)-1°(R5)-1°R6)*.
Обґрунтувати замкнутість підмножини А’ безлічі P(А) щодо відповідності g:
A = {a, b, c, d, e}, A’ÍA2, g = (A2, A, G), G = {((A1, A2), {A3, A4})ÎG| A1, A2ÍA і A3 = A1ÈA2 і A4 = A1ÇA2};
A = N, A’ÍN2, g = (A2, A, G), G = {((A1, A2), A3)ÎG| A1, A2ÍA і A3 = A1+A2};
A – безліч чорних ворон, A’ÍА2, g = (A2, A, G), G = {((A1, A2), A3)ÎG| A1, A2ÍA і A1, A2 - батьки A3}.
Спеціальні функції
Задачі
Записати в матричному виді і визначити, чи є наступні відповідності підстановками:
g1 = ({1, 2, 3, 4, 5}, {1, 2, 3, 4, 5}, {(1, 2), (2, 3), (3, 5), (5, 1), (4, 4)});
g2 = ({1, 2, 3, 4}, {1, 2, 3, 4}, {(1, 2), (2, 3), (4, 2), (3, 3)});
g4 = ({1, 2, 3, 4}, {1, 2, 3, 4, 5}, {(1, 2), (2, 3), (2, 5), (4, 4), (3, 5), (5, 2)});
g3 = ({1, 2, 3, 4, 5, 6, 7}, {1, 2, 3, 4, 5, 6, 7}, {(1, 4), (2, 3), (3, 2), (4, 6), (6, 5), (5, 1), (7, 7)});
g5 = ({1, 2, 3, 4, 5}, {1, 2, 3, 4, 5}, {(1, 5), (5, 2), (2, 1), (2, 4), (3, 4), (4, 3)}).
Привести підстановку g1 до підстановки g2 за допомогою операцій перестановки і циклу:
g1 = ({a, b, c, d, e}, {a, b, c, d, e}, {(a, c), (c, d), (d, a), (b, e), (e, b)}), g2 = ({a, b, c, d, e}, {a, b, c, d, e}, {(a, d), (d, a), (b, b), (c, e), (e, c)});
g1 = ({a, b, c, d}, {a, b, c, d}, {(a, a), (b c), (c, b), (d, d)}), g2 = ({a, b, c, d, e}, {a, b, c, d, e}, {(a, c), (c, b), (b, d), (d, e), (e, a)});
g1 = ({1, 2, 3, 4, 5}, {1, 2, 3, 4, 5}, {(1, 2), (2, 3), (3, 5), (4, 4), (5, 1)}), g2 = ({1, 2, 3, 4, 5}, {1, 2, 3, 4, 5}, {(1, 4), (4, 1), (2, 3), (3, 5), (5, 2)})
Визначити існуючі цикли і нестаціонарні елементи в підстановках задач 1, 2.
Визначити, чи є послідовностями:
список студентів академічної групи;
латинський алфавіт;
унарні і бінарні операції мови Java (C);
періодична таблиця Менделєєва;
генеалогічне дерево.
Визначити, чи є функціоналами:
нормальний розподіл Гаусса;
виконання популярних пісень за заявками радіослухачів;
відповідності виду g1: (AÞB)ÞC, AÞ(BÞC), (AÞB)Þ(CÞD);
програми мовою Java (C) і їх вхідні і відповідні вихідні дані - Program((Input(Output);
успішність студентів LearnÞRating і професійна діяльність фахівців WorkÞSuccess.
Визначити, чи є відповідності g відображеннями, що зберігають еквівалентність:
;g1: ПроцесориÞКомп'ютери, r1 - відношення еквівалентності різних процесорів за продуктивністю і r2 - відношення еквівалентності різних комп'ютерів за обчислювальною потужністю.
g2: СтудентиÞПотоки (року навчання), r3 - відношення еквівалентності обсягу знань студентів і r4 - відношення еквівалентності в підготовці до професійної діяльності між однаковими потоками різних факультетів.
Операції
Задачі
Представити в префіксній і постфіксній формах арифметичні вираження і побудувати для них дерева обчислень:
a/(b-c*d)+(a*b*(d-c));
(a-b-c)*((b+d/a)*a-c);
((a+d)*b-c)/(b-a+c/d);
b+(a/(b+c-d))*(a/(c+d));
(a/((b+c)/d))*(b*c+a)/d;
d+((b*c)/(a*b-d))*(a+b).
Визначити правильність завдання бінарних операцій і їхню комутативність, знайти одиницю (нуль), зворотний елемент:
x°y º x-y і x, yÎN;
x°y º (x*y)-1 і x, yÎC;
x°y º max(x, y) і x, yÎN;
x°y º Ö(x2+y2) і x, yÎD и x³0;
x°y º x/y і x, yÎR і x>0.
Перевірити, чи є операція j, що визначена на безлічі A = {a, b, c}, асоціативною, комутативною і чи має одиничний елемент
j = {((a, a), b), ((a, b), c), ((a, c), a), ((b, a), c), ((b, b), a), ((b, c), b), ((c, a), a), ((c, b), b), ((c, c), c)}.
Довести, що операція y = ((a*b)-1)/(a+b), визначена на безлічі [1, ¥), асоціативна.
Нехай асоціативна операція °на безлічі А с одиницею е така, що кожен елемент аÎА є оборотний, зворотний позначається як а'. Показати, що (a°b)’ = b’°a’.
Показати, що якщо операція ° – асоціативна операція на безлічі А з одиницею е така, що а°а = е для будь-якого аÎА, то ° комутативна.
Нехай є асоціативна операція на безлічі А така, що для будь-яких а,bÎА, якщо а°b = b°а, то а = b. Показати, що кожен елемент А ідемпотентен стосовно °. Що можна сказати про операцію °, якщо вона має одиницю?
КОМБІНАТОРИКА
Перестановки
Задачі
Нехай А и В - кінцеві безлічі, що складаються з m і n елементів відповідно:
Чому дорівнює число відповідностей між А и В?
Скільки існує функцій з А и В?
Скільки існує 1-1 функцій з А и В?
При яких m і n існує взаємооднозначна відповідність між А и В?
Нехай безліч А1 містить n1 елементів; безліч А2 - n2 елементів;...., безліч Аm - nm елементів. Скільки елементів містить їхній декартовий добуток А1´А2´...´Аm ?
Скільки елементів містить безліч Аn , якщо |А| = S?
Чому дорівнює число відповідностей між m - елементною безліччю А і n - елементною безліччю В:
функціональних (ін’єктивних);
усюди визначених (сюр’єктивних).
Чому дорівнює число відношень між m - елементами безлічі А и n - елементами безлічі В?
Чому дорівнює число відношень на n-елементної безлічі?
Скількома способами можна скласти чотирикольоровий прапор, якщо існує матеріал семи кольорів веселки? Вирішити задачу за умови:
одна зі смуг прапора повинна бути зеленою чи червоною;
дві зі смуг повинні бути голубою і жовтою;
три смуги повинні бути синьою, зеленою і жовтою.
Скільки різних слів можна одержати, переставляючи букви в слові «математика».
Сполучення
Задачі
Довести, що безліч з n елементів має 2n підмножин.
Скільки підмножин з k елементів має безліч з n елементів?
Чому дорівнює число всіляких проекцій кортежу довжини n?
У футбольній команді є 13 гравців і 2 воротарі. Скількома способами можна вибрати граючий склад (11 гравців, у тому числі один воротар)?
Визначити число всіляких наборів з п'яти різних елементів по трьох, якщо в кожнім наборі:
усі предмети різні;
однакові предмети можуть повторюватися.
Рекуррентные співвідношення
Задачи
В офісі є дев'ять робочих місць, з яких на двох можуть працювати тільки жінки, на трьох — тільки чоловіки і на чотирьох — чоловіки і жінки. Скількома способами можна розподілити трьох жінок і чотирьох чоловіків на ціх місцях?
Покажіть, що число сполучень з п елементів по r дорівнює числу n-перестановок з повтореннями з r елементів одного типу і n - r елементів іншого типу, тобто
Біном Ньютона
Задачі
Визначити за допомогою біноміальних коефіцієнтів число наборів з п'яти різних елементів по три, якщо в кожнім наборі:
усі предмети різні;
однакові предмети можуть повторюватися.
Довести властивості біноміальних коефіцієнтів:
C(n, k) = C(n, n-k);
C(n, k)*C(k, r) = C(n-r, k-r)*C(n, r).
Поліноміальні і експонентні виробляючі функції
Задачі
Нехай у сполучення з повтореннями з п елементів по r повинні обов'язково входити елементи k фіксованих типів (k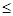 
п). Показати, що число таких сполучень дорівнює С(r + п – k - 1, r—k). Зокрема, якщо в кожне сполучення повинний входити хоча б один елемент кожного з п типів (це можливо тільки при п £ r), то число таких сполучень дорівнює С(r – 1, r - п).
Вираз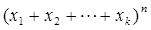 
розкладається в суму членів виду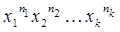 
з деякими коефіцієнтами, де числа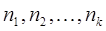 
приймають усілякі значення від 0 до п, причому 
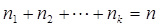. Покажіть, що для даного розкладання:
коефіцієнт при члені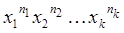 
дорівнює числу перестановок з повтореннями з n елементів зі специфікацією 
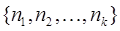, тобто
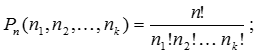
кількість усіх членів дорівнює числу n-сполучень з повтореннями з k елементів, тобто
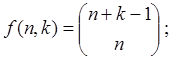
сума всіх коефіцієнтів дорівнює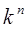 
.
На підставі співвідношень попередньої задачі для вираження (а + 3b + 5з - d)6 визначити:
коефіцієнти при членах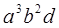 
і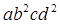 
;
кількість усіх членів розкладання.
Принцип включення і виключення
Задачі
З 30 співробітників англійську мову знають 19, німецьку— 17, французьку— 11, англійську і німецьку— 12, англійську і французьку — 7, німецьку і французьку — 5, усі три мови — 2. Скільки співробітників не володіють іноземними мовами? Скільки з них знають тільки англійську, тільки німецьку, тільки французьку мови?
Показати, що число натуральних чисел, що поділяються на n і не переважає x, дорівнює [x/n].
Знайти число цілих позитивних чисел, що не перевершують 200 і не поділяються на жодне з чисел 3, 5, 7.
Знайти число простих чисел, що не перевершують 250.
Розбивки
Задачі
N урн випадковим образом заповнюються п кулями (n < N). Знайти імовірність того, що кожна з п перших урн буде містити точно по одній кулі, якщо урна може прийняти:
не більше однієї кулі;
будь-яке число куль, яке не перевищує п.
Покажіть, що
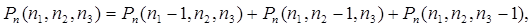
Знайти число способів розподілу 23 студентів у групи по 3 і 5 чоловік.
БулЄва АЛГЕБРА
Функції
Задачі
Побудувати таблиці істинності для формул:
(P®Q)Ú(P®(QÙP));
ù(P®ù(QÙP))®(PÚR);
(P®Q~R))®((P®Q)~(P®R));
(PÙ(QÚùP))Ù((Q®P)ÚQ)).
Довести виконуємость формул:
ù(P®ùP);
(P®Q)®(Q®P);
(Q®(PÙR))Ù((PÚR)®Q).
Довести тотожну істинність формул:
(P®Q)Ú(Q®P);
P®(Q®(PÙQ));
(Q®R)®((PÚQ)®(PÚR));
(P®R)®((Q®R)®((P(Q)®R))).
Довести еквівалентність:
(AÚ(BÚC))~((AÙB)Ú(AÙC));
(AÚ(BÙC))~((AÚB)Ù(AÚC));
(AÚ(BÙA))~A;
(AÙ(AÚC)Ù(BÚC))~((AÙB)Ú(AÙC));
((AÚB)Ù(AÚB))~A.
Способи завдання булєвих функцій
Задачі
Представити функції алгебри логіки (ФАЛ), що рівні 1 на наступних наборах аргументів х1х2х3 і х1х2х3х4, у табличному, графічному і чисельному виді:
001, 010, 110, 011;
100, 010, 000;
0001, 0100, 0110, 1011, 1101;
0010, 0101, 1000, 1001, 1100, 1111.
Представити задані ФАЛ у табличному, графічному і чисельному виді:
ù(x1+ù(x1x2x3+ùx3));
x1x2+ù(x2x3+x1+ùx2ùx3);
(x1Åx2)x3+(x1Åx3)x2;
(x1+x2)(x1x2+ùx2x3);
x1+ùx2+x3;
(ùx1+x2)(ùx2+x3);
ù(ùx1ùx2ùx1)+(ùx1+ùx2+ùx3).
Записати СДНФ і СКНФ ФАЛ, що рівні 1 на наступних наборах аргументів х1х2х3 і х1х2х3х4:
1. 001, 010, 110, 011;
1. 100, 010, 000;
2. 0001, 0100, 0110, 1011, 1101;
3. 0010, 0101, 1000, 1001, 1100, 1111.
Записати в ДНФ наступні ФАЛ:
[(x2®x1)~x3]+(x4 /x1);
ù(ùx1~(ùx2+x3))(x1®x4);
(x1+ùx2)x3+(ùx3+ùx4)(ùx1+x3ùx4);
ù(x1+ù(x1x2x3+ùx3));
x1x2+ù(x2x3+x1+ùx2ùx3);
ù(x1ùx2)ù(x1ùx3+(x3x4));
x1ùx3+ù(x1ùx2+ùx1x3)+x2x3x4(x1+ùx1x2x3);
(x1Åx2)x3+(x1Åx3)x2;
(x1¯x2)/x3+(ùx2®x3)¯x4;
ù((x1+ùx2+x3+x4)(x1+x2+x3+ùx4))+(x1x3x4®0).
Записати в КНФ ФАЛ з попередньої задачі.
Для ФАЛ f(x1, x2, x3), заданих у табл. 3.1. (таблиці істинності), записати СДНФ і СКНФ.
Таблиця 3.1
| X1 | ||||||||
| X2 | ||||||||
| X3 | ||||||||
| F1 | ||||||||
| F2 | ||||||||
| F3 | ||||||||
| F4 |
Записати в СДНФ наступні ФАЛ:
x1x2+ùx1ùx3+x2x3+ùx2ùx3;
(x1+x2)(x1x2+ùx2x3);
(x1ùx2+x3x4)(x2+x4)(x1+ùx3+ùx4);
x1+ùx2+x3;
(ùx1+x2)(ùx2+x3);
ù(ùx1ùx2ùx1)+(ùx1+ùx2+ùx3);
x1(x2+ùx4)+x1(x1+x3);
ùx2(x1ùx4+x3x4)+ùx1[ùx3(ùx2+x4)+x2x3x4]+x1x2(ùx3+x4).
Записати в СКНФ ФАЛ із задачі 6.
Записати СДНФ і СКНФ ФАЛ задачі 3.
Записати в СДНФ і СКНФ ФАЛ, задані в цифровій формі:
1. f(x1,..., x4) = Ú(0, 1, 3, 5, 9, 12, 14);
2. f(x1,..., x4) = Ú(1, 4, 6, 8, 10, 13, 15);
3. f(x1,..., x4) = Ú(0, 2, 5, 7, 8, 10, 11, 14);
4. f(x1,..., x4) = Ú(1, 3, 4, 7, 9, 12, 13, 15);
5. f(x1,..., x4) = Ù(2, 5, 7, 9, 12, 14, 15);
6. f(x1,..., x4) = Ù(1, 2, 4, 5, 7, 8, 9, 12, 14);
7. f(x1,..., x4) = Ù(3, 4, 6, 9, 11, 13, 14, 15);
8. f(x1,..., x4) = Ù(2, 5, 8, 10, 12, 13, 14).
По заданих СДНФ знайти СКНФ наступних ФАЛ:
a) f(x1, x2, x3) = ùx1ùx2ùx3+ x1x2ùx3+x1ùx2x3+ùx1x2x3;
a) f(x1, x2, x3) = ùx1ùx2x3+x1ùx2x3+x1x2ùx3;
b) f(x1, x2, x3) = x1x2ùx3+ùx1ùx2x3;
c) f(x1, x2, x3) = ùx1ùx2x3+ùx1x2ùx3+ùx1x2x3+x1x2x3.
Показати, що якщо в СДНФ знак Ú скрізь замінити на знак Å, то вийде формула, еквівалентна вихідної. Чи справедливо аналогічне твердження для довільної ДНФ?
Булєва алгебра
Задачі
Методом перебору довести справедливість основних законів алгебри логіки (властивості 1-18).
Методом перебору довести, що всі елементарні ФАЛ можуть бути виражені через операції {Ú, Ù, ù} у такий спосіб:
x1®x2 = ùx1+x2;
x1x2 = x1ùx2 (жоден із засобів);
x1~x2 = x1x2+ùx1ùx2 = (x1+ùx2) (ùx1+x2);
x1Åx2 = x1ùx2+ùx1x2 = (x1+x2)(ùx1+ùx2);
x1/x2 = ù(x1x2) = ùx1+ùx2;
x1¯x2 = ù(x1+x2)= ùx1ùx2.
Довести наступні тотожності аналітично і методом перебору:
a) x1+ùx1x2 = x1+x2;
a) x1(x1+ùx1x2 ) = x1;
b) (x1 + ùx1ùx2)(x1+ùx1+x2)= x1+ùx2;
c) x1(x1+ùx1x2 )(ùx1+x2ùx2) = 0;
d) ùx1+ùx1x2+x1(x1+x2)+ùx1(ùx1+ùx2) = 1;
e) (x1+ùx1)(x2+ùx2)(x3+ùx3) = 1.
Чи справедливі комутативний, асоціативний і дистрибутивний закони стосовно наступних логічних операцій:
еквівалентність;
сума по модулі 2 (нееквівалентність);
стрілка Пірса;
штрих Шеффера;
імплікація;
зворотна імплікація (заборона).
Асоціативний закон для операцій /, ¯ несправедливий. Чи мають місце співвідношення, схожі з асоціативним законом?
x1¯x2¯x3 = (x1¯x2) ¯x3 = x1¯(x2¯x3);
x1¯x2¯x3¯x4 = (x1¯x2)¯(x3¯x4);
x1/x2/x3 = (x1/x2)/x3 = x1/(x2/x3);
x1/x2/x3/x4 = (x1/x2)/(x3/x4).
Чи зв'язані між собою співвідношеннями, що подібні з законом інверсії, операції /, ¯, а також ®,?
ù(x1¯x2) = ùx1/ùx2;
ù(x1/x2) = ùx1¯ùx2;
ù(x1®x2) = ùx1ùx2;
ù(x1x2) = ùx1®ùx2.
Довести наступні тотожності:
ù(x1¯x2) = x1+x2;
ù(x1/x2) = x1x2;
x1/(x2¯x3) = (ùx1¯x2)(ùx1¯x3);
x1Åx2Åx1x2 = x1+x2;
x1~x2 = ù(x1Åx2);
x1Åx2 = ù(x1~x2).
Довести справедливість співвідношень:
ù(ùx1x2) = x1+x2;
ù(x1®ùx2) = x1 x2;
x1®x2®x1 = x1;
x1x2x1 = x1
ùx1®x2 = x1+x2;
x1 ùx2 = x1x2.
Перевірити, чи справедливі наступні співвідношення:
x1+(x2~x3) = (x1+x2)~(x1+x3);
x1®(x2~x3) = (x1®x2)~(x1®x3);
x1(x2~x3) = x1x2~x1x3;
x1Å(x2®x3 ) = (x1Åx2)®(x1Åx3);
x1®(x2®x3) = (x1®x2)®(x1®x3).
Визначити значення ФАЛ а) на непарних номерах наборів (1,3,5,…);
