Задано линейное интегральное уравнение Фредгольма второго рода
, (6)
где y(t), K(t,s) – заданные функции, x(t) – искомая функция, λ – числовой параметр.
Запишем уравнение (6) в виде
, (7)
где отображение 
, X – банахово пространство. Предположим, что параметр λ, ядро K(t,s) таковы, что отображение F является сжимающим с коэффициентом сжатия λ. Тогда уравнение (6) имеет единственное решение, которое можно найти методом последовательных приближений с помощью следующих рекуррентных соотношений:
(8)
Приближения (8) сходятся к решению уравнения (6) с некоторой скоростью, причем величина погрешности n -го приближения определяется неравенством
, (9)
где 
- нулевое приближение, которое выбирается произвольным образом.
Задание 1
Задание: Определить, при каких 
для следующих интегральных уравнений Фредгольма 2-го рода в пространстве C[0, 1], 
[0, 1] можно применить метод сжимающих отображений. При 
найти приближенное решение методом последовательных приближений с точностью 
, сравнить его с точным решением: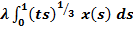 
+ 
Решение:
Рассмотрим пространство C[0, 1]. Определим 
, при которых применим метод сжимающих отображений для данного уравнения.
F(x) = 
+ 
;
= 
= 
≤ 
= 
.
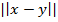≤ 1 => ≤ 
.
Т.е. при ≤ применим метод сжимающих отображений.
Положим 
, тогда 
. Оценим нужное количество итераций с помощью неравенства (положив 
= 0, тогда 
= , и 
= 1):
≤ 0,001 => 
≤ 
.
Следовательно, 
будет решением с требуемой точностью.
С помощью программы посчитаем 
(t) = 0.214239 t1/3+t2
Листинг 1: Программа для вычисления приближённой функции x(t) (Wolfram Mathematica 7.0):
Clear[x,t];
x[t_]=0;
For[i=1,i<=8,i++,
x[t_] = 0.5*Integrate[(t*s)^(1/3)*x[s], {s, 0, 1}]+t^2;
];
Print[x[t]];
Сравним это решение с точным. Положим C = 
, тогда 
.
Подставив 
в исходное уравнение, получим:
(1.1)
Тогда 
= 4.6E-5 ≤ 0,001.
Рассмотрим пространство [0, 1]. Оценим ядро:
= 
= 
≤ 1.
Т.е. F(x) отображает [0, 1] на себя и является сжимающим при 
≤ 
. Поэтому при к данному уравнению можно применить метод сжимающих отображений. В данном случае понадобится число итераций, определяемое соотношением:
< 0,001 (1.2)
Откуда получаем: 
= 
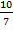
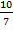
< 0,001.
Т.е. при n = 6 достигается требуемая точность.
Задание 2
Задание: Вычислить приближенное решение уравнения с точностью 0,01:
. (2.1)
Приведём это уравнение к виду 
. Сделаем это, выразив 
:
(2.2)
Найдём 
и радиус 
такие, что шар B[ , ] инвариантен относительно отображения F и в этом шаре F – сжимающее. Т.к. F является дифференцируемой, то в качестве константы Липшица можно взять 
.
В данном случае 
= - 
. Выберем центр шара = -1, выберем из следующих условий:
(2.3)
= 
, 
. Тогда:
(2.4)
Выберем одно из решений системы, например, r = 1. Тогда отрезок [-2, 0] инвариантен относительно отображения F, на нём отображение F – сжимающее, и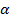 
= 
. Оценим расстояние:
(2.5)
То есть при n = 6 будет достигнута требуемая точность.
С помощью программы посчитаем :
Листинг 2: Программа для вычисления приближённого значения одного из корней (Wolfram Mathematica 7.0):
Clear [F, x];
F[x_]=(1./8)*(-2*x^2-5);
x = -1;
For [i=1, i£6, i++,
x = F[x];
];
Print [x];
На выходе получаем, что 
. Тогда по теореме Виетта мы можем вычислить второй корень 
.
Ответ: , .
Задание 3
Задание: Определить, является ли отображение f нормированного пространства Е на себя сжимающим. Вычислить 
, где 
= 
, = 0, и оценить расстояние от до неподвижной точки.
Е = [-1, 1], 
.
Решение: Проверим, является ли f сжимающим.
= 
≤ 
.
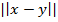То есть f является сжимающим отображением с коэффициентом 
.
Тогда:
= 0,
= 
,
= 
,
= 
.
Оценим расстояние от до неподвижной точки:
= 
= 0.3363.
Задание 4
Задание: Выяснить, является ли отображение F: X -> Y непрерывным, равномерно непрерывным, удовлетворяющим условию Липшица.
X = C[-2, 4], Y = C[-2, 4], F(x) = 
.
Решение: Проверим, удовлетворяет ли отображение условию Липшица.
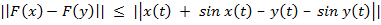
Т.е. удовлетворяет, и константа Липшица 
Т.к. отображение удовлетворяет условию Липшица, то оно равномерно непрерывно, т.е. для любого ε существует
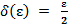, что при 
=> 
≤ ε.
Т.к. отображение равномерно непрерывное, то оно является и непрерывным.
