Отображения в нормированных векторных пространствах
Отчет по лабораторной работе №4
(«Функциональный анализ»)
Студента 3 курса 6 группы
Работа сдана 1 декабря 2010 г. Преподаватель:
__ зачтена ____________2010 г. Чеб Елена Сергеевна
доцент кафедры МФ,
----------------------------------------- кандидат физ.-мат.наук
(подпись преподавателя)
Минск 2010
СОДЕРЖАНИЕ
Теория………………………………………………………………………………………………..3
Задание 1…………………………………………………………………………………………….5
Задание 2…………………………………………………………………………………………….6
Задание 3…………………………………………………………………………………………….8
Задание 4…………………………………………………………………………………………….8
Теория
Принцип сжимающих отображений в нормированных векторных пространствах.
Пусть в банаховом пространстве Е действует отображение f. Точка x* называется неподвижной точкой отображения f, если 
.
Таким образом, неподвижные точки отображения f – это решение уравнения 
.
Будем говорить, что отображение f является сжимающим (сжатием), если существует постоянная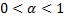 
такая, что выполняется неравенство 
для всех 
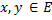. Число α называется коэффициентом сжатия.
Теорема 1 (принцип сжимающих отображений). Пусть f отображает замкнутое в банаховом пространстве E множество M на себя и является на M сжимающим с коэффициентом сжатия α. Тогда в M отображение f имеет единственную неподвижную точку 
, которая может быть найдена методом последовательных приближений по формуле 
, где 
и 
при 
. Кроме того, справедлива оценка скорости сходимости
.
Следствие 1. Пусть f отображает банахово пространство E само на себя и является сжатием. Тогда f имеет в E единственную неподвижную точку.
Следствие 2. Пусть f определено на шаре 
, где E – банахово пространство. Пусть f является на 
сжатием с коэффициентом α и при этом выполнено условие 
. Тогда в шаре 
существует единственная точка отображения f, которая может быть найдена методом последовательных приближений.
Теорема 2. В пространстве 
непрерывное отображение замкнутого шара на себя имеет неподвижную точку.
Теорема 3. Пусть f отображает замкнутое множество M⊂E на себя и при некотором 
отображение 
является на M сжатием. Тогда в M существует единственная неподвижная точка f.
Следствие 3. Пусть f отображает замкнутое выпуклое множество M⊂E на себя, причем на M оно непрерывно дифференцируемо и 
. Тогда справедливы утверждения теоремы 3.
Применение принципа сжимающих отображений к интегральным уравнениям.
Рассмотрим интегральное уравнение вида
(1)
Здесь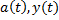 
- заданные функции; K(t,s,x(s)) – заданная функция, называемая ядром интегрального уравнения; x(t) – неизвестная функция.
Решение 
разыскивается в различных пространствах функций в зависимости от свойств функции K(t,s,z) и y. Пространства выбираются так, чтобы интеграл в (1) существовал. Уравнение (1) называется интегральным уравнением Фредгольма. Если 
, то уравнение (1) называется интегральным уравнением Фредгольма 1-го рода, соответственно при 
- 2-го рода и при 
- уравнением 3-го рода. Интегральное уравнение (1) называется линейным, если функция K(t,s,z) линейна по z. Если 
, то уравнение (1) называется однородным.
Уравнение вида
, (2)
Называется интегральным уравнением Вольтерра. Уравнение Вольтерра является частным случаем уравнения Фредгольма.
Решением уравнений (1) и (2) называется функция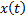 
, при подстановке которой в уравнение выполняется равенство для всех 
или почти всех. Линейное однородное уравнение всегда имеет решение 
.
Остановимся на применении метода последовательных приближений к интегральным уравнениям 2-го рода.
Рассмотрим линейное неоднородное интегральное уравнение Фредгольма 2-го рода:
. (3)
Теорема 4. Пусть K(t,s) – непрерывная функция на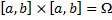 
и 
, тогда для любого параметра λ такого, что
, интегральное уравнение Фредгольма 2-го рода (3) имеет единственное непрерывное решение для любой правой части 
.
Рассмотрим нелинейное уравнение Фредгольма 2-го рода:
. (4)
Теорема 5. Пусть K(t,s,z) – непрерывная функция переменных t,s,z, удовлетворяющая условию Липшица по z, то есть существует постоянная
L > 0 такая, что 
. Если выполнено условие L(b-a)|λ|<1, то интегральное уравнение (4) имеет единственное непрерывное решение для любой функции .
Рассмотрим линейное неоднородное уравнение Вольтерра
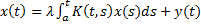. (5)
Теорема 6. Пусть K(t,s) – непрерывная функция по переменным t и s. Тогда для любой функции и любого параметра λ интегральное уравнение Вольтерра 2-го рода (5) имеет единственное непрерывное решение.
