Цель: изучить основные возможности приложения Microsoft Excel для решения систем линейных уравнений.
Задание
Найти решение системы линейных уравнений:

Методические указания
1. Создать таблицу, как показано на рис.7.1. Коэффициенты при неизвестных X1, X2, X3 занести в столбцы A, B, C соответственно, а свободные члены – в столбец E. В столбец D занести формулы вычисления левой части каждого уравнения системы, где в качестве искомых корней X1, X2, X3 используются ячейки A6, B6, C6 соответственно.

Рис.7.1. Панель интерфейса Microsoft Excel в режиме проверки формул
2. Дать команду Сервис\Поиск решения….
3. В открывшемся диалоговом окне Поиск решения… ввести необходимые параметры процесса вычисления: в поле Установить целевую ячейку указать адрес ячейки, в которую занесена целевая функция – левая часть любого уравнения системы ($D$2, $D$3 или $D$4), установить переключатель Равной: в положение (значению:), а в поле ввода занести соответствующее значение свободного члена (3, 1 или 8). В поле Изменяя ячейки указать диапазон ячеек, в которых будет находится искомое решение ($A$6:$C$6). В поле Ограничения указать $D$2:$D$4=$E$2:$E$4, как показано на рис.7.2.

Рис.7.2.Панель установки необходимых параметров процесса вычисления
4. После установки всех параметров, необходимых для решения системы уравнений, нажать кнопку получения решения. Полученные результаты оформить так, как показано на рис.7.3.
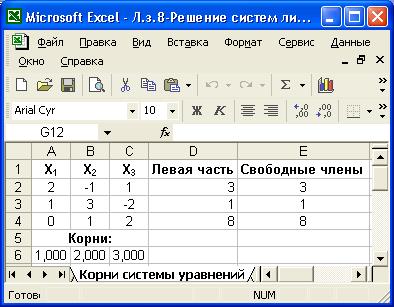
Рис.7.3. Результаты вычисления корней системы линейных уравнений.
Занятие №7
Оптимизация
Цель: изучить основные возможности приложения Microsoft Excel для нахождения оптимального решения задач линейного программирования.
Задание
Цех предприятия производит в месяц два вида товаров. На производстве действуют ограничения по сырью, трудовым ресурсам и транспортным расходам:
1. Для производства объема X1 товара первого вида необходимо 3 единицы сырья, объема X2 товара второго вида – 6 единиц сырья. Всего цех располагает 18 единицами сырья.
2. Для изготовления объема X1 товара первого вида требуется 6 рабочих, объема X2 товара второго вида - 4 рабочих. В цехе 24 рабочих.
3. Транспортные расходы на перевозку объема X1 товара первого вида составляют 2 единицы, объема X2 товара второго вида – 1 единицу. Эти затраты не могут быть менее 2-х единиц (цена аренды одного автомобиля минимальной грузоподъемности в течение дня). Вся дневная продукция цеха может быть вывезена на одном автомобиле.
Найти оптимальные объемы X1 и X2 производства этих товаров с целью получения максимальной прибыли. Прибыль от реализации объема X1 первого вида товара составляет 5 единиц, а от реализации объема X2 второго вида товара - 5,5 единиц.
Методические указания
Математические соотношения, связывающие искомые объемы X1 и X2 производства товаров и величину прибыли с учетом ограничений, составляют задачу линейного программирования. К задаче линейного программирования сводятся многие задачи оптимального использования производственных мощностей, задачи о составлении оптимальных смесей, а также линейные транспортные задачи.
Линейным программированием называется раздел математики, в котором изучаются методы нахождения минимума или максимума линейной функции конечного числа переменных при условии, что переменные удовлетворяют конечному числу условий (ограничений), имеющих вид линейных уравнений или линейных неравенств.
Математическая модель задачи поиска оптимальных объемов X1 и X2 производства товаров с целью получения максимальной прибыли в терминах задачи линейного программирования запишется следующим образом:
1) ограничения по сырью: 3x1+6x2≤18;
2) ограничения по трудовым ресурсам: 6x1+4x2≤24;
3) ограничения на транспортные расходы: 2x1+x2≥2;
4) ограничения на объемы производства: x1≥0; x2≥0;
5) целевая функция – прибыль: Qmax(x1,x2)=5x1+5,5x2.
1. Создать таблицу, как показано на рис.8.1.

Рис.8.1. Панель интерфейса Microsoft Excel в режиме проверки формул
Ограничения заносятся в верхнюю часть таблицы. Коэффициенты отношений – в область C2:D4, правая часть неравенств – в F2:F4. Коэффициенты целевой функции заносятся в C6,D6. В процессе расчетов в области E2:E4 отображаются вычисляемые (фактические) значения правой части неравенств.
2. Дать команду Сервис\Поиск решения….
3. В открывшемся диалоговом окне Поиск решения… ввести необходимые параметры процесса вычисления: в поле Установить целевую ячейку указать адрес ячейки, в которую занесена целевая функция $E$6, установить переключатель Равной: в положение (Max). В поле Изменяя ячейки указать диапазон ячеек, в которых будет находится искомое решение ($C$7:$D$7). Ограниченияустанавливаются с помощью кнопки Добавить, как показано на рис.8.2.

Рис.8.2.Панель ввода ограничений
4. После установки всех параметров, необходимых для получения решения, панель должна выглядеть так, как показано на рис. 8.3.

Рис.8.3.Панель установки необходимых параметров процесса вычисления
5. Нажать кнопку получения решения. Если вычисления оказались успешными, Microsoft Excel выведет окно итогов, показанное на рис.8.4. Итоги можно сохранить или отказаться от них. Кроме того, можно получить один из трех видов отчетов (Результаты, Устойчивость, Пределы), которые позволят лучше осмыслить полученные результаты, в том числе оценить их достоверность.

Рис.8.4. Окно итогов
6. На рис.8.5 показаны окончательные результаты решения поставленной задачи.

Рис.8.5.Результаты решения задачи
Таким образом, как следует из рис.8.5, максимальное значение целевой функции (прибыли) Qmax(x1,x2) =23,25 при x1= 3 и x2 =1,5.
Вопросы для самоконтроля
1. Какая команда меню выполняет решение задачи оптимизации?
2. Какие параметры необходимо задать в диалоговом окне Поиск решения…?
3. Каким образом осуществляется ввод, изменение или удаление ограничений?
4. Как правильно интерпретировать результаты решения?
Литература
1. Информатика: Базовый курс/ С.В. Симонович и др. – СПб.: Питер, 2001,-640с.
2. Microsoft Excel 2000: справочник. Под ред. Ю. Колесникова.-СПб.: Питер, 1999, 480с.
3. Рычков В. Самоучитель Excel 2000..-СПб.: Питер, 1999, 336с.
4. Попов А.А. Excel: практическое руководство. -ДЕСС КОМ.: Москва, 2001, 302с.
Содержание
Аннотация 2
1. Занятие №2. Итоговые вычисления 7
2. Занятие №3. Использование функций 12
3. Занятие №4. Табулирование функций и построение графиков 15
4. Занятие №5. Решение нелинейных уравнений 18
5. Занятие №6. Решение систем нелинейных уравнений 25
6. Занятие №7. Решение систем линейных уравнений 26
7. Занятие №8. Оптимизация 27
Литература 31






