Цель: изучить основные возможности приложения Microsoft Excel для решения нелинейных уравнений.
Задание
Найти все действительные корни нелинейного уравнения 
с относительной погрешностью 
.
Методические указания
1. Построить график функции 
как показано на рис.5.1.
Рис. 5.1. Результаты табулирования и построения графика функции
2. Пользуясь графиком, определить точки, в которых значения функции равны нулю: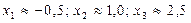 
– это и есть приближенные значения корней уравнения.
3. Уточнить значения корней с заданной относительной погрешностью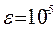 
. Для этого открыть новый лист и назвать его, например, Корни уравнения. Будем искать вычисленные значения корней в ячейке A1, а уравнение занесем в ячейку B1.
4. Занести в ячейку A1 приближенное значение первого корня: -0,5.
5. В ячейку B1 занести левую часть уравнения, используя в качестве независимой переменной x адрес ячейки A1.
6. В меню Сервис\Параметры…\Вычисления в поле Относительная погрешность: установить значение 0,00001.
7. Дать команду Сервис\Подбор параметра….
8. В открывшемся диалоговом окне Подбор параметра в поле Установить в ячейке: указать адрес ячейки, в которую занесена левая часть уравнения (B1), в поле Значение: задать значение правой части уравнения (0), а в поле Изменяя значение ячейки: указать адрес ячейки, в которую занесен аргумент (A1).
9. Щелкнуть на кнопке OK и проанализировать результат, отображаемый в диалоговом окне Результат подбора параметра. Щелкнуть на кнопке OK, чтобы сохранить полученные значения ячеек, участвовавших в операции.
10. Повторить расчет, задавая в ячейке A1 приближенные значения корней 1,0 и 2,5. Полученные результаты занести в таблицу, как показано на рис. 5.2.
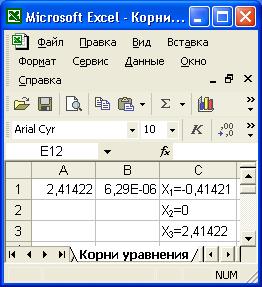
Рис.5.2. Результаты вычисления корней нелинейного уравнения
Вопросы для самоконтроля
1. Как определить приближенные значения корней нелинейного уравнения?
2. Сколько ячеек используется при уточнении корня нелинейного уравнения, и какую информацию необходимо в них задавать?
3. Какие значения необходимо устанавливать в диалоговом окне Подбор параметра?
4. Каким образом устанавливается заданное значение относительной погрешности вычисления корня 
?
5. Почему при решении нелинейных уравнений для различных значений начальных приближений могут получаться разные результаты?
Занятие №5
Решение систем нелинейных уравнений
Цель: изучить основные возможности приложения Microsoft Excel для решения систем нелинейных уравнений.
Задание
Найти решение системы нелинейных уравнений:
Методические указания
1. Преобразовать исходную систему уравнений к виду
2. Построить графики функци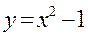й 
и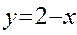 
, как показано на рис.6.1.
Рис.6.1. Результаты табулирования и построения графиков функци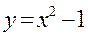й и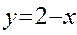
3. Пользуясь графиком, определить точки, в которых функции пересекаются: 
– это и есть приближенные значения корней системы уравнений.
4. Уточнить значение корней. Для этого открыть новый лист и назвать его, например, Корни системы уравнений.
5. Будем искать вычисленное значение корня x1 в ячейке A16. Занести в ячейку A16 приближенное значение первого корня: -2,0. В ячейки B16 и B17 занести обе функции, которые в качестве аргумента x ссылаются на ячейку A16. Для организации процесса вычислений в ячейку C16 ввести целевую функцию, которая вычисляет среднее отклонение значений функций друг от друга (рис.6.2). Очевидно, если эти функции пересекаются (т.е. имеются решения), C16 =0.
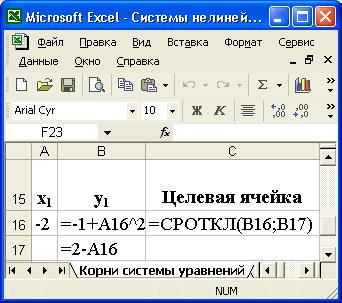
Рис.6.2. Панель интерфейса Microsoft Excel в режиме проверки формул.
6. Дать команду Сервис\Поиск решения….
7. Для уточнения корня в открывшемся диалоговом окне Поиск решения… ввести необходимые параметры процесса вычисления: в поле Установить целевую ячейку указать адрес ячейки, в которую занесена целевая функция ($C$16), установить переключатель Равной: в положение (минимальное значение), а в поле Изменяя ячейки указать адрес ячейки, в которую занесен аргумент ($A$16). Результат вычислений существенно зависит от начального приближения, заданного в качестве решения. На рис.6.3 приведены исходный и конечный вид таблицы, если задать начальное значение корня x1, равным -2.
Рис.6.3. Начальный и конечный вид таблицы вычисления корня x1 системы нелинейных уравнений
8. Повторить расчет, задавая приближенное значение корня x2= 2. Полученные результаты занести в таблицу, как показано на рис. 6.4.
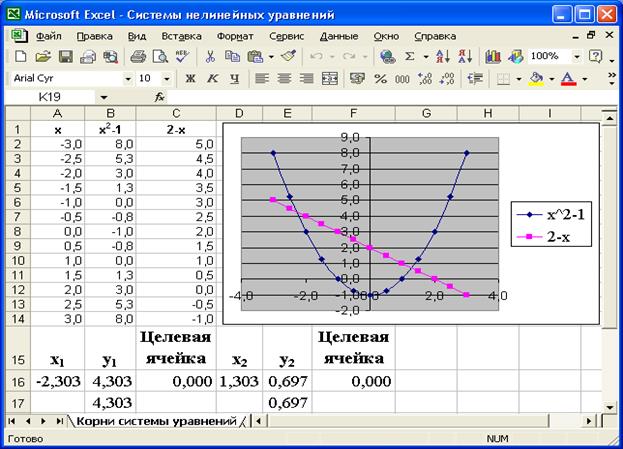
Рис.6.4 Результаты вычисления корней системы нелинейных уравнений.
Вопросы для самоконтроля
1. Как определить приближенные значения корней системы нелинейных уравнений?
2. Почему при решении системы нелинейных уравнений для различных значений начальных приближений могут получаться разные результаты?
3. Сколько ячеек используется при уточнении корня системы нелинейных уравнений, и какую информацию необходимо в них задавать?
4. Какие значения необходимо устанавливать в диалоговом окне Поиск решения?
Лабораторное занятие №6
