Основные понятия.
Момент силы относительно оси вращения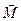 
– это векторное призведение радиус-вектора на силу.
(1.14)
Момент силы – это вектор, направление которого определяется по правилу буравчика (правого винта) в зависимости от направления силы, действующей на тело. Момент силы направлен вдоль оси вращения и не имеет конкретной точки приложения.
Численное значение данного вектора определяется по формуле:
M=r×F × sina (1.15),
где a - угол между радиус-вектором и направлением действия силы.
Если a=0 или p, момент силы М=0, т.е. сила, проходящяя через ось вращения или совпадающяя с ней, вращения не вызывает.
Наибольший по модулю вращающий момент создается, если сила действует под углом a=p/2 (М > 0) или a=3p/2 (М < 0).
Используя понятие плеча силы (плечо силы d – это перпендикуляр, опущенный из центра вращения на линию действия силы), формула момента силы принимает вид:
, где 
(1.16)
Правило моментов сил (условие равновесия тела, имеющего неподвижную ось вращения):
Для того, чтобы тело, имеющее неподвижную ось вращения, находилось в равновесии, необходимо, чтобы алгебраическая сумма моментов сил, действующих на данное тело, равнялась нулю.
S Мi =0 (1.17)
Единицей измерения момента силы в системе СИ является [Н×м]
При вращательном движении инертность тела зависит не только от его массы, но и от распределения ее в пространстве относительно оси вращения.
Инертность при вращении характеризуется моментом инерциитела относительно оси вращения J.
Момент инерции материальной точки относительно оси вращения – это величина, равная произведению массы точки на квадрат ее расстояния от оси вращения:
Ji=mi× ri2 (1.18)
Моментом инерции тела относительно оси называется сумма моментов инерции материальных точек, из которых состоит тело:
J=S mi× ri2 (1.19)
Момент инерции тела зависит от его массы и формы, а также от выбора оси вращения. Для определения момента инерции тела относительно некоторой оси используется теорема Штейнера-Гюйгенса:
J=J0+m× d2 (1.20),
где J0 – момент инерции относительно параллельной оси, проходящей через цент масс тела, d – расстояние между двумя параллельными осями. Момент инерции в СИ измеряется в [кг×м2]
Момент инерции при вращательном движении туловища человека определяют опытным путем и рассчитывают приблизительно по формулам для цилиндра, круглого стержня или шара.
Момент инерции человека относительно вертикальной оси вращения, которая проходит через центр масс (центр масс тела человека находится в сагиттальной плоскости немного впереди второго крестцового позвонка), в зависимости от положения человека, имеет следующие значения: при стойке “смирно” – 1,2 кг×м2; при позе «арабеск» – 8 кг×м2; в горизонтальном положении – 17 кг × м2.
Работа во вращательном движении совершается при вращении тела под действием внешних сил.
Элементарная работа силы во вращательном движении равна произведению момента силы на элементарный угол поворота тела:
dAi=Mi× dj (1.21)
Если на тело действует несколько сил, то элементарная работа равнодействующей всех приложенных сил определяется по формуле:
dA=M× dj (1.22),
где М – суммарный момент всех внешних сил, действующих на тело.
Кинетическая энергия вращающегося тела Wк зависит от момента инерции тела и угловой скорости его вращения:
(1.23)
Момент импульса (момент количества движения) 
– величина, численно равная произведению импульса тела на радиус вращения.
L=p× r=m× V× r (1.24).
После соответствующих преобразований можно записать формулу для определения момента импульса в виде:
(1.25).
Момент импульса 
– вектор, направление которого определяется по правилу правого винта. Единицей измерения момента импульса в СИ является [кг×м2/с]
Основные законы динамики вращательного движения.
Основное уравнение динамики вращательного движения:
Угловое ускорение тела, совершающего вращательное движение, прямо пропорционально суммарному моменту всех внешних сил и обратно пропорционально моменту инерции тела.
(1.26).
Данное уравнение играет ту же роль при описании вращательного движения, что и второй закон Ньютона для поступательного движения. Из уравнения видно, что при действии внешних сил угловое ускорение тем больше, чем меньше момент инерции тела.
Второй закон Ньютона для динамики вращательного движения можно записать в ином виде:
(1.27),
т.е. первая производная от момента импульса тела по времени равна суммарному моменту всех внешних сил, действующих на данное тело.
Закон сохранения момента импульса тела:
Если суммарный момент всех внешних сил, действующих на тело, равен нулю, т.е.
S Mi =0, тогда dL/dt=0 (1.28).
Из этого следует 
или 
(1.29).
Это утверждение составляет сущность закона сохранения момента импульса тела, который формулируется следующим образом:
Момент импульса тела остается постоянным, если суммарный момент внешних сил, действующих на вращающееся тело, равен нулю.
Этот закон является справедливым не только для абсолютно твердого тела. Примером является фигурист, который выполняет вращение вокруг вертикальной оси. Прижимая руки, фигурист уменьшает момент инерции и увеличивает угловую скорость. Чтобы затормозить вращения, он, наоборот, широко разводит руки; в результате момент инерции увеличивается, и угловая скорость вращения уменьшается.
В заключение приведем сравнительную таблицу основных величин и законов, характеризующих динамику поступательного и вращательного движений.
Таблица 1.4.
| Поступательное движение | Вращательное движение | ||
| Физическая величина | Формула | Физическая величина | Формула |
| Масса | m | Момент инерции | J=m×r2 |
| Сила | F | Момент силы | M=F×r, если 
|
| Импульс тела (количество движения) | p=m×V | Момент импульса тела | L=m×V×r; L=J×w |
| Кинетическая энергия |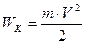 
| Кинетическая энергия | 
|
| Механическая работа | dA=FdS | Механическая работа | dA=Mdj |
| Основное уравнение динамики поступательного движения | 
| Основное уравнение динамики вращательного движения | 
 ,
|
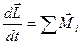| Закон сохранения импульса тела |  или
 если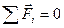 
| Закон сохранения момента импульса тела |  или SJiwi=const,
если 
|
Центрифугирование.
Разделение неоднородных систем, состоящих из частиц различной плотности, может быть произведено под действием силы тяжести и силы Архимеда (выталкивающей силы). Если есть водная суспензия частиц различной плотности, то на них действует результирующая сила
Fр=Fт – FА=r1×V×g - r×V×g, т.е
Fр=(r1 - r)× V ×g (1.30)
где V – объем частицы, r1 и r – соответственно плотности вещества частицы и воды. Если плотности незначительно отличаются друг от друга, то результирующая сила мала и расслоение (осаждение) происходит достаточно медленно. Поэтому используют принудительное разделение частиц за счет вращения разделяемой среды.
Центрифугированием называется процесс разделения (сепарации) неоднородных систем, смесей или взвесей, состоящих из частиц различной массы, происходящий под действием центробежной силы инерции.
Основу центрифуги составляет ротор с гнездами для пробирок, расположенный в закрытом корпусе, который приводится во вращение электродвигателем. При вращении с достаточно высокой скоростью ротора центрифуги частицы взвеси, различные по масссе, под действием центробежной силы инерции распределяются слоями на различной глубине, а наиболее тяжелые осаждаются на дне пробирки.
Можно показать, что сила, под действием которой происходит сепарация, определяется по формуле:
(1.31)
где w - угловая скорость вращения центрифуги, r – расстояние от оси вращения. Эффект центрифугирования тем больше, чем больше различие плотностей сепарируемых частиц и жидкости, а также существенно зависит от угловой скорости вращения.
Ультрацентрифуги, работающие при скорости вращения ротора порядка 105–106 оборотов в минуту, способны разделить частицы размером менее 100нм, взвешенные или растворенные в жидкости. Они нашли широкое применение в медико-биологических исследованиях.
С помощью ультрацентрифугирования можно разделить клетки на органеллы и макромолекулы. Вначале оседают (седиментируют) более крупные части (ядра, цитоскелет). При дальнейшем увеличении скорости центрифугирования последовательно оседают более мелкие частицы – сначала митохондрии, лизосомы, затем микросомы и, наконец, рибосомы и крупные макромолекулы. При центрифугировании различные фракции оседают с различной скоростью, образуя в пробирке отдельные полосы, которые можно выделить и исследовать. Фракционированные клеточные экстракты (бесклеточные системы) широко используют для изучения внутриклеточных процессов, например для изучения биосинтеза белка, расшифровки генетического кода.
Для стерилизации наконечников в стоматологии используется масляный стерилизатор с центрифугой, с помощью которой удаляется излишнее масло.
Центрифугирование можно использовать для осаждения частиц, взвешенных в моче; отделения форменных элементов от плазмы крови; разделения биополимеров, вирусов и субклеточных структур; контроля за чистотой препарата.
Задания для самоконтроля знаний.
Задание1. Вопросы для самоконтроля.
Чем отличается равномерное движение по окружности от равномерного прямолинейного движения? При каком условии тело будет двигаться равномерно по окружности?
Объясните причину того, что равномерное движение по окружности происходит с ускорением.
Может ли криволинейное движение происходить без ускорения?
При каком условии момент силы равен нулю? принимает наибольшее значение?
Укажите границы применимости закона сохранения импульса, момента импульса.
Укажите особенности сепарации под действием силы тяжести.
Почему разделение белков с различными молекулярными массами можно проводить при помощи центрифугирования, а метод фракционной перегонки оказывается неприемлемым?
Задание 2. Тесты для самоконтроля.
Вставьте пропущенное слово:
Изменение знака угловой скорости свидетельствует об изменении_ _ _ _ _ вращательного движения.
Изменение знака углового ускорения свидетельствует об изменении_ _ _ вращательного движения
Угловая скорость равна _ _ _ _ _производной угла поворота радиус-вектора по времени.
Угловое ускорение равно _ _ _ _ _ _производной угла поворота радиус-вектора по времени.
Момент силы равен_ _ _ _ _, если направление действующей на тело силы совпадает с осью вращения.
Найдите правильный ответ:
Момент силы зависит только от точки приложения силы.
Момент инерции тела зависит только от массы тела.
Равномерное движение по окружности происходит без ускорения.
А. Правильно. В. Неправильно.
Скалярними являются все перечисленные величины, за исключением
А. момента силы;
В. механической работы;
С. потенциальной энергии;
Д. момента инерции.
Векторными величинами являются
А. угловая скорость;
В. угловое ускорение;
С. момент силы;
Д. момент импульса.
Ответы: 1 – направления; 2 – характера; 3 – первой; 4 – второй; 5 – нулю; 6 – В; 7 – В; 8 – В; 9 – А; 10 – А, В, С, Д.
Задание 3. Получите связь между единицами измерения:
линейной скорости см/мин и м/с;
углового ускорения рад/мин2 и рад/с2;
момента силы кН×см и Н×м;
импульса тела г×см/с и кг×м/с;
момента инерции г×см2 и кг×м2.
Задание 4. Задачи медико-биологического содержания.
Задача №1. Почему в полетной фазе прыжка спортсмен не может никакими движениями изменить траекторию движения центра тяжести тела? Совершают ли мышцы спортсмена работу при изменении положения частей тела в пространстве?
Ответ: Движениями в свободном полете по параболе спортсмен может только изменять расположение тела и его отдельных частей относительно своего центра тяжести, который в данном случае является центром вращения. Спортсмен совершает работу по изменению кинетической энергии вращения тела.
Задача №2. Какую среднюю мощность развивает человек при ходьбе, если продолжительность шага 0,5с? Считать, что работа затрачивается на ускорение и замедление нижних конечностей. Угловое перемещение ног около Dj=30о. Момент инерции нижней конечности равен 1,7кг × м2. Движение ног рассматривать как равнопеременное вращательное.
Решение:
1)Запишем краткое условие задачи: Dt= 0,5с; Dj =300= p/ 6; I =1,7кг × м2
2) Определим работу за один шаг (правая и левая нога): A= 2 ×Iw2/ 2 =Iw2.
Используя формулу средней угловой скорости wср=Dj/Dt, получим: w= 2 wср= 2 ×Dj/Dt; N=A/Dt= 4 ×I×(Dj)2/(Dt)3
3) Подставим числовые значения: N =4 × 1,7 × (3,14)2/(0,53 × 36)=14,9(Вт)
Ответ: 14,9 Вт.
Задача №3. Какова роль движения рук при ходьбе?
Ответ: Движение ног, перемещающихся в двух параллельных плоскостях, находящихся на некотором расстоянии друг от друга, создает момент сил, стремящийся повернуть корпус человека вокруг вертикальной оси. Руками человек размахивает «навстречу» движению ног, создавая тем самым момент сил противоположного знака.
Задача №4. Одним из направлений усовершенствования бормашин, применяемых в стоматологии, является увеличение скорости вращения бора. Скорость вращения борного наконечника в ножных бормашинах составляет 1500 оборотов в минуту, в стационарных электробормашинах – 4000 об/мин, в турбинных бормашинах – уже достигает 300000 об/мин. Зачем разрабатываются новые модификации бормашин с большим числом оборотов в единицу времени?
Ответ: Дентин в несколько тысяч раз более восприимчив к болевым ощущениям, чем кожа: на 1мм2 кожи приходится 1-2 болевые точки, а на 1мм2 дентина резцов – до 30000 болевых точек. Увеличение числа оборотов по данным физиологов уменьшает боль при обработке кариозной полости.
З адание 5 . Заполните таблицы:
Таблица №1. Проведите аналогию между линейными и угловыми характеристиками вращательного движения и укажите связь между ними.
| Линейные характеристики | Линейная скорость V | Тангенциальное ускорение at | Сила F | Импульс тела p | Кинетичес-кая энергия Wk |
| Угловые характеристики | |||||
| Связь между ними |
Таблица №2.
| Закон | Формула | Формулировка | Границы применимости |
| Закон сохранения импульса | |||
| Закон сохранения момента импульса | |||
| Основное уравнение динамики поступательного движения | |||
| Основное уравнение динамики вращательного движения |
Задание 6. Заполните ориентировочную карту действия:
| Основные задания | Указания | Ответы |
| Для чего в начальной стадии исполнения сальто гимнаст сгинает колени и прижимает их к груди, а в конце вращения выпрямляет тело? | Используйте для анализа процесса понятие момента импульса и закон сохранения момента импульса. | |
| Объясните, почему стоять на цыпочках (или держать тяжелый груз) так тяжело? | Рассмотрите условия равновесия сил и их моментов. | |
| Как изменится угловое ускорение при увеличении момента инерции тела? | Проанализируйте основное уравнение динамики вращательного движения. | |
| Как зависит эффект центрифугирования от разности в плотностях жидкости и частиц, которые сепарируются? | Рассмотрите силы, действующие при центрифугировании и соотношения между ними |
Глава 2. Основы биомеханики.
Вопросы.
Рычаги и сочленения в опорно-двигательном аппарате человека. Понятие о степенях свободы.
Виды сокращения мышц. Основные физические величины, описывающие мышечные сокращения.
Принципы двигательной регуляции у человека.
Методы и приборы для измерения биомеханических характеристик.
Содержание темы.
2.1. Рычаги и сочленения в опорно-двигательном аппарате человека.
Анатомия и физиология двигательного аппарата человека обладают следующими особенностями, которые необходимо учитывать при биомеханических расчетах: движения тела определяются не только мышечными силами, но и внешними силами реакции, силой тяжести, инерционными силами, а также упругими силами и трением; структура двигательного аппарата допускает исключительно вращательные движения. С помощью анализа кинематических цепей поступательные движения могут быть сведены к вращательным движениям в суставах; движения управляются с помощью очень сложного кибернетического механизма, так что происходит постоянное изменение ускорений.
Опорно-двигательный аппарат человека состоит из сочлененных между собой костей скелета, к которым в определенных точках прикрепляются мышцы. Кости скелета действуют как рычаги, которые имеют точку опоры в сочленениях и приводятся в движение силой тяги, возникающей при сокращении мышц. Различают три вида рычага:
1) Рычаг, к которому действующая сила F и сила сопротивления R приложены по разные стороны от точки опоры. Примером такого рычага является череп, рассматриваемый в сагиттальной плоскости.
2) Рычаг, у которого действующая сила F и сила сопротивления R приложены по одну сторону от точки опоры, причем, сила F приложена к концу рычага, а сила R - ближе к точке опоры. Данный рычаг дает выигрыш в силе и проигрыш в расстоянии, т.е. является рычагом силы. Пример - действие свода стопы при подъеме на полупальцы, рычаги челюстно-лицевого отдела (рис. 2.1). Движения жевательного аппарата очень сложны. При закрывании рта поднимание нижней челюсти из положения максимального опускания до положения полного смыкания ее зубов с зубами верхней челюсти осуществляется движением мышц, поднимающих нижнюю челюсть. Эти мышцы действуют на нижнюю челюсть как на рычаг второго рода с точкой опоры в суставе (дающий выигрыш при жевании в силе).
3) Рычаг, у которого действующая сила приложена ближе к точке опоры, чем сила сопротивления. Данный рычаг является рычагом скорости, т.к. дает проигрыш в силе, но выигрыш в перемещении. Пример - кости предплечья.
Рис. 2.1. Рычаги челюстно-лицевого отдела и свода стопы.
Большинство костей скелета находится под действием нескольких мышц, развивающих усилия по различным направлениям. Равнодействующая их находится путем геометрического сложения по правилу параллелограмма.
Кости опорно-двигательного аппарата соединяются между собой в сочленениях или суставах. Концы костей, образующих сустав, удерживаются вместе с помощью плотно охватывающей их суставной сумки, а также прикрепленных к костям связок. Для уменьшения трения соприкасающиеся поверхности костей покрыты гладким хрящом и между ними имеется тонкий слой клейкой жидкости.
Первой ступенью биомеханического анализа двигательных процессов является определение их кинематики. На основе такого анализа строятся абстрактные кинематические цепи, подвижность или устойчивость которых может быть проверена исходя из геометрических соображений. Различают замкнутые и разомкнутые кинематические цепи, образуемые суставами и расположенными между ними жесткими звеньями.
Состояние свободной материальной точки в трехмерном пространстве задается тремя независимыми координатами – х, y, z. Независимые переменные, которые характеризуют состояние механической системы, называются степенями свободы. У более сложных систем количество степеней свободы может быть выше. Вообще, количество степеней свободы определяет не только количество независимых переменных (что характеризует состояние механической системы), но и количество независимых перемещений системы.
Число степеней свободы является основной механической характеристикой сустава, т.е. определяет число осей, вокруг которых возможно взаимное вращение сочленненых костей. Обусловлено оно главным образом геометрической формой поверхности костей, соприкасающихся в суставе.
Максимальное число степеней свободы в суставах – 3.
Примерами одноосного (плоского) сочленения в организме человека являются плечелоктевое, надпяточное и фаланговые соединения. Они допускают только возможность сгибания и разгибания с одной степенью свободы. Так, локтевая кость с помощью полукруглой выемки охватывает цилиндрический выступ на плечевой кости, который и служит осью сустава. Движения в суставе – сгибание и разгибание в плоскости, перпендикулярной оси сустава.
Лучезапястный сустав, в котором осуществляется сгибание и разгибание, а также приведение и отведение, можно отнести к суставам с двумя степенями свободы.
К суставам с тремя степенями свободы (пространственное сочленение) относятся тазобедренное и лопаточно-плечевое сочленение. Например, в лопаточно-плечевом сочленении шаровидная головка плечевой кости входит в сферическую впадину выступа лопатки. Движения в суставе – сгибание и разгибание (в сагиттальной плоскости), приведение и отведение (в фронтальной плоскости) и вращение конечности вокруг продольной оси.
Замкнутые плоские кинематические цепи обладают числом степеней свободы fF, которое вычисляется по числу звеньев n следующим образом:
(2.1)
Ситуация для кинематических цепей в пространстве более сложная. Здесь выполняется соотношение
(2.2)
где fi - число ограничений степеней свободы i- го звена.
В любом теле можно выбрать такие оси, направление которых при вращении будет сохраняться без любых специальных устройств. Они имеют название свободные оси вращения. Тело любой формы всегда имеет три взаимно перпендикулярные оси вращения, которые могут быть свободными осями вращения. Они проходят через центр масс и называются главными осями инерции. При этом наиболее устойчивым будет вращение вокруг оси с наибольшим моментом инерции.
