Для определения координат потре-бителя необходимо знать координаты спутников (не менее 4) и дальность от потребителя до каждого видимого спутника. Для того, чтобы потребитель мог определить координаты спутников, излучаемые ими навигационные сигналы моделируются сообщениями о параметрах их движения. В аппаратуре потребителя происходит выделение этих сообщений и определение координат спутников на нужный момент времени.
Координаты и составляющие вектора скорости меняются очень быстро, поэтому сообщения о параметрах движения спутников содержат сведения не об их координатах и составляющих вектора скорости, а информацию о параметрах некоторой модели, аппроксимирующей траекторию движения КА на до-статочно большом интервале времени (около 30 минут). Параметры аппроксимирующей модели меняются достаточно медленно, и их можно считать постоянными на интервале аппроксимации.
Параметры аппроксимирующей мо-дели входят в состав навигационных сообщений спутников. В системе GPS используется Кеплеровская модель движения с оскулирующими элементами. В этом случае траектория полёта КА разбивается на участки аппроксимации длительностью в один час. В центре каждого участка задаётся узловой момент времени, значение которого сообщается потребителю навигационной информации. Помимо этого, потребителю сообщают параметры модели оскулирующих элементов на узловой момент времени, а также параметры функций, аппроксимирующих изменения параметров модели оскулирующих элементов во времени как предшествующем узловому элементу, так и следующем за ним.
В аппаратуре потребителя выделяется интервал времени между моментом времени, на который нужно определить положение спут-ника, и узловым моментом. Затем с помощью аппроксимирующих функций и их параметров, выделенных из навигационного сообщения, вычисляются значения параметров модели оскулирующих элементов на нужный момент времени. На пос-леднем этапе с помощью обычных формул кеплеровской модели определяют координаты и составляющие вектора скорости спутника.
В системе Глонасс для определения точного положения спутника используются дифференциальные модели движения. В этих моделях координаты и составляющие вектора скорости спутника определяются численным интегрированием дифференциальных уравнений движения КА, учитывающих конечное число сил, действующих на КА. Начальные условия интегрирования задаются на узловой момент времени, располагающийся посередине интервала ап-проксимации.
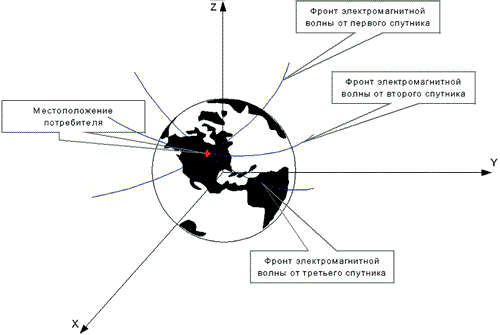
Как было сказано выше, для определения координат потребителя необходимо знать координаты спутников (не менее 4) и дальность от потребителя до каждого видимого спутника, которая определяется в навигационном приёмнике [4] с точностью около 1 м. Для удобства рассмотрим простейший “плоский” случай, представленный на рис. 8.