При работе с матрицами, необходимо их описать (тип элементов матрицы, количество строк и столбцов), осуществить ввод элементов матрицы. Если вам безразличны значения элементов матриц, можно осуществить ввод, используя датчик случайных чисел. Ниже приведен пример такого ввода:
Program Matrix1;
Uses crt;
Const n=5;
Var i, j: Integer;
A: Array [1..n, 1..n] of integer;
Begin
ClrScr;
Randomize; {инициализация встроенного датчика случайных чисел }
{Ввод матрицы}
For i:=1 to n do
For j:=1 to n do
A[i,j]:=Random(20); {A[i,j] получает случайное значение, не превосходящее 20}
{ Вывод матрицы на экран по строкам}
For i:=1 to n do
Begin
For j:=1 to n do write(A[i,j]:5);
Writeln;
End;
End.
Типичными операциями над матрицами являются нахождение суммы элементов строки, умножение матрицы на вектор и т.п.
Пример. Суммирование элементов заданной строки матрицы.
s:=0;
for j:=1 to n do s:=s+b[i,j]; {суммируется i-я строка}
Пример. Умножение матрицы на вектор.
For i:=1 to n do
Begin
s:=0;
For j:=1 to n do s:=s+A[i,j]*B[j];
C[i]:=s;
end;
Целью данной работы является получение практических навыков работы с матрицами.
Задачи.
1. Дана действительная матрица 
размера n*n. Получить действительную матрицу 
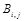, элемент которой b[i,j] равен наибольшему элементу данной матрицы, расположенному в области, определяемой индексами i,j так, как показано на рисунке 2,в.
2. Будем называть соседями элемента с индексами i,j некоторой матрицы такие элементы этой матрицы, соответствующие индексы которых отличаются от i и j не более чем на 1. Для данной целочисленной матрицы размером n*m найти матрицу из 0 и 1 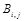, элемент которой b[i,j] равен 1, когда среди соседей a[i,j] есть не менее двух совпадающих.
3. Дана действительная матрица размера n*n. Получить действительную матрицу 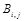, элемент которой b[i,j] равен сумме элементов данной матрицы, расположенных в области, определяемой индексами i,j так, как показано на рисунке 2,а.
4. Дана действительная матрица порядка 2*n. Получить новую матрицу, переставляя ее блоки размера n*n в соответствии с рисунком 1,а.
5. В данной действительной матрице размера 6*9 поменять местами строку, содержащую элемент с наибольшим значением, со строкой, содержащей наименьший элемент.Предполагается, что эти элементы единственны.
6. В данной квадратной целочисленной матрице порядка 17 указать индексы всех элементов с наибольшим значением.
7. Дана действительная матрица размера n*n. Получить действительную матрицу 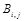, элемент которой b[i,j] равен сумме элементов данной матрицы, расположенных в области, определяемой индексами i,j так, как показано на рисунке 2,б.
8. Будем называть соседями элемента с индексами i,j некоторой матрицы такие элементы этой матрицы, соответствующие индексы которых отличаются от i и j не более чем на 1. Для данной целочисленной матрицы размером n*m найти матрицу из 0 и 1 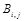, элемент которой b[i,j] равен 1, когда все соседи a[i,j] и само a[i,j] равны 0.
9. Дана действительная матрица порядка 2*n. Получить новую матрицу, переставляя ее блоки размера n*n в соответствии с рисунком 1,б.
10. Элемент матрицы назовем седловой точкой, если он является наибольшим в своем столбце и одновременно наименьшим в своей строке. Для заданной цело матрицы размером 10*15 напечатать индексы всех ее седловых точек.
11. Дана действительная матрица размера n*n. Получить действительную матрицу 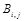, элемент которой b[i,j] равен сумме элементов данной матрицы, расположенных в области, определяемой индексами i,j так, как показано на рисунке 2,в.
12. Будем называть соседями элемента с индексами i,j некоторой матрицы такие элементы этой матрицы, соответствующие индексы которых отличаются от i и j не более чем на 1. Для данной целочисленной матрицы размером n*m найти матрицу из 0 и 1 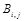, элемент которой b[i,j] равен 1, когда все соседи a[i,j] меньше самого a[i,j].
13. Дана действительная матрица размера m*n, все элементы которой различны. В каждой строке выбирается элемент с наибольшим значением, затем среди этих чисел выбирается наименьшее. Указать индексы элемента с найденным значением.
14. Дана действительная матрица размера n*n. Получить действительную матрицу 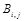, элемент которой b[i,j] равен наибольшему элементу данной матрицы, расположенному в области, определяемой индексами i,j так, как показано на рисунке 2,а.
15. Дана действительная матрица порядка 2*n. Получить новую матрицу, переставляя ее блоки размера n*n в соответствии с рисунком 1,в.
16. В данной действительной матрице порядка n найти сумму элементов строки, в которой располагается элемент с наименьшим значением.
17. Дана действительная матрица размера n*n. Получить действительную матрицу 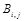, элемент которой b[i,j] равен наибольшему элементу данной матрицы, расположенному в области, определяемой индексами i,j так, как показано на рисунке 2,б.
18. Дана целочисленная матрица размером 7*4. Переставляя ее строки и столбцы, добиться того, чтобы наибольший элемент (один из них) оказался в верхнем левом углу.
19. Дана действительная матрица порядка 2*n. Получить новую матрицу, переставляя ее блоки размера n*n в соответствии с рисунком 1,г.
20. Дана действительная матрица размера n*n. Получить действительную матрицу 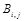, элемент которой b[i,j] равен сумме элементов данной матрицы, расположенных в области, определяемой индексами i,j так, как показано на рисунке 2,г.
