Работа N 1. Разветвления
Независимость программы от данных часто требует в зависимости от конкретного набора данных (или промежуточных результатов) выбирать один из двух или более различных вариантов, вычислительного процесса, т.е. осуществлять разветвление вычислительного процесса. В языке PASCAL для таких случаев предусмотрены условный оператор, оператор выбора варианта и оператор перехода.
Условный оператор может принимать одну из двух конструкций:
| IF B THEN S1 ELSE S2 IF B THEN S1 |
где B - логическое выражение, а S1, S2 - операторы. Эти операторы могут быть простыми или составными (т.е. сгруппированными вместе при помощи операторных скобок Begin End).
В первом варианте если логическое выражение истинно, то выполняется оператор S1, если логическое выражение ложно, то выполняется оператор S2.
Пример. Вычислить A=k+40, если 15<k<25. При всех других значениях k A=20*k.
Условный оператор имеет вид
If (k>15) And (k<25) Then A:= K+40 Else A:= 20*k
Другой вариант решения этой же задачи предполагает использование краткой формы условного оператора
A:= 20*k
If (k>15) And (k<25) Then A:=K+40
Оператор выбора варианта используется в тех случаях, когда в зависимости от значения какого-либо выражения необходимо выполнить один из нескольких операторов. Этот оператор имеет вид:
| Case (селектор) OF (список констант 1): (Оператор 1); (список констант 2): (Оператор 2); ........... (список констант N): (Оператор N); End; |
Если значение селектора равно одной из констант, то выполняется оператор помеченный этой константой.
Пример. Пусть k - переменная целого типа.
Case k of
1: A:=Sin(x);
2, 3: A:=Sin(x)+2;
4..10, 15: A:=Cos(x)+Sin(x);
End;
Если требуется нарушить естественный порядок выполнения операторов можно воспользоваться оператором безусловного перехода, имеющим вид GOTO (Метка)
Метка является числом или идентификатором, описанным в разделе описания меток, например
Label 10, 20, Lab1, Metka;
Целью данной работы является получение практических навыков использования условных операторов и операторов выбора.
Задание. Напишите программу решения задачи, с использованием операторов организующих разветвления.
Варианты заданий.
1. Если сумма трех попарно различных чисел x, y, z меньше 10, то наименьшее из этих трех чисел заменить полусуммой двух других, в противном случае заменить меньшее из x и y полусуммой двух оставшихся значений.
2. Для заданного числа a найти корень уравнения f(x)=0, где

3. Дано число х. Напечатать в порядке возрастания числа ch(x), 1+│x│, (1+x2)x.
4. Даны числа A1, B1, C1, A2, B2, C2. Напечатать координаты точки пересечения прямых, описываемых уравнениями A1*X + B1*Y + C1 = 0 A2*X + B2*Y + C2 = 0 либо сообщить, что эти прямые совпадают, не пересекаются либо вообще не существуют.
5. Даны произвольные числа a, b, c. Если нельзя построить треугольник с такими длинами сторон, то сообщить об этом, в противном случае сообщить является ли треугольник равносторонним, равнобедренным или треугольником общего вида.
6. Даны действительные числа x, y. Определить принадлежит ли точка с координатами (x, y) заштрихованной части плоскости рис.1, а.
7. Даны действительные числа x, y. Определить принадлежит ли точка с координатами (x, y) заштрихованной части плоскости рис.1, б.
8. Даны действительные числа x, y. Определить принадлежит ли точка с координатами (x, y) заштрихованной части плоскости рис.1, в.
9. Даны действительные числа x, y. Определить принадлежит ли точка с координатами (x, y) заштрихованной части плоскости рис.1, г.
10. Даны действительные числа x, y. Определить принадлежит ли точка с координатами (x, y) заштрихованной части плоскости рис.1, д.
11.Даны действительные числа x, y. Определить принадлежит ли точка с координатами (x, y) заштрихованной части плоскости рис.1, е.
12.Даны действительные числа x, y. Определить принадлежит ли точка с координатами (x, y) заштрихованной части плоскости рис.1, ж.
13.Даны действительные числа x, y. Определить принадлежит ли точка с координатами (x, y) заштрихованной части плоскости рис.1, з.

14.Пусть D-заштрихованная часть плоскости (рис 2. а) и пусть U определяется по x, y следующим 0, если (x, y)ÎD, u= x, в противном случае. Даны действительные числа х,у. Определить U.
15.Пусть D-заштрихованная часть плоскости (рис 2. б) и пусть U определяется по x, y следующим образом-3, если (x, y) ÎD, u= y*y, в противном случае. Даны действительные числа х,у. Определить U.
16.Пусть D-заштрихованная часть плоскости (рис 2. б) и пусть U определяется по x, y следующим образом
x-y, если (x, y) ÎD, u= y*x+7, в противном случае. Даны действительные числа х,у. Определить U.
17.Пусть D-заштрихованная часть плоскости (рис 2. б) и пусть U определяется по x, y следующим образом x*x-1, если (x, y) ÎD, u= │x-1│, в противном случае. Даны действительные числа х,у. Определить U.
18.Пусть D-заштрихованная часть плоскости (рис 2. б) и пусть U определяется по x, y следующим образом x*x-1│, если (x, y) ÎD, u= x+y, в противном случае. Даны действительные числа х,у. Определить U.
19.Пусть D-заштрихованная часть плоскости (рис 2. б) и пусть U определяется по x, y следующим образомx+y, если (x, y) ÎD, u= x-y, в противном случае. Даны действительные числа х,у. Определить U.
20.Известно, что астрологи делят год на 12 периодов и каждому из них ставят в соответствие один из знаков Зодиака.
| 20.01 | - | 18.02 | - | Водолей | 23.07 | - | 22.08 | - | Лев | |
| 19.02 | - | 20.03 | - | Рыбы | 23.08 | - | 22.09 | - | Дева | |
| 21.03 | - | 19.04 | - | Овен | 23.09 | - | 22.10 | - | Весы | |
| 20.04 | - | 20.05 | - | Телец | 23.10 | - | 22.11 | - | Скорпион | |
| 21.05 | - | 21.06 | - | Близнецы | 23.11 | - | 21.12 | - | Стрелец | |
| 22.06- | - | 22.07 | - | Рак | 22.12 | - | 19.01 | - | Козерог |
Напишите программу, которая вводит дату некоторого дня года и печатает название соответствующего знака Зодиака.

Работа N2. Циклы.
Сочетания цикла и разветвления.
При решении многих задач вычислительный процесс может иметь циклический характер. Это означает, что часть операторов многократно выполняется при различных значениях переменных. В языке PASCAL имеется три вида операторов цикла: оператор с предварительным условием (While), оператор с последующим условием (Repeat), оператор цикла с параметром (For).
Операторы для записи циклов являются сложными, так как в их состав входят другие операторы.
Для всех операторов цикла характерна следующая особенность. Повторяющиеся вычисления записываются всего один раз. Вход в цикл возможен только через его начало. Переменные цикла должны быть определены до входа в циклическую часть. Необходимо предусмотреть выход из из цикла: или по естественному его окончанию, или по оператору перехода.
Форма записи оператора цикла с предусловием:
| While <логическое выражение> do begin <операторы циклической части> end; |
Например, найти наименьшее положительное число для данной ЭВМ.
Program MinEps;
var Eps, Eps_Min: real;
begin
Eps:=1;
While Eps>0 do {Заголовок оператора цикла}
begin
Eps_Min:=Eps; {Тело оператора цикла }
Eps:=Eps/2;
end;
writeln('Eps_Min=', Eps_Min);
end.
Форма записи оператора цикла с постусловием:
| Repeat < операторы циклической части> Until < логическое выражение > |
Например, найти наименьшее положительное число для данной ЭВМ.
Program MinEps;
var Eps_Min: real;
begin
Eps_Min:=1;
Repeat {Заголовок оператора цикла}
Eps_Min:=Eps_Min/2; {Тело оператора цикла }
Until Min_Eps/2=0;
writeln('Eps_Min=', Eps_Min);
end.
Оператор цикла с параметром используется в тех случаях, когда известно заранее число повторений. Существует два варианта оператора:
1. используется при изменении переменной цикла i по возрастанию
| For i:=m1 to m2 do begin <операторы циклической части> end; |
2. используется при изменении переменной цикла i по убыванию
| For i:=m1 Downto m2 do begin <операторы циклической части> end; |
Например, вычислить сумму первых 10 натуральных чисел
Program Sum10;
var i, Sum:integer;
begin
Sum:=0;
For i:=1 to 10 do
Sum:=Sum+i;
writeln('Сумма=', Sum);
end.
Замечание. Если циклическая часть оператора цикла состоит из одного оператора, операторные скобки Begin - End можно не использовать.
Целью данной работы является получение практических навыков использования операторов цикла.
ЗАДАНИЕ. Напишите программу решения задачи, с использованием операторов организующих циклические вычисления.
ВАРИАНТЫ ЗАДАНИЙ.
1. Дано натуральное число N. Вычислить
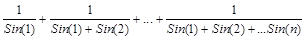
2. Дано натуральное число N. Вычислить  N корней
N корней
3. Дано натуральное число n. Вычислить 
4. Дано натуральное число n. Вычислить a (a+1)... (a+n-1)
5. Дано натуральное число N и действительное число x. Вычислить Sin(x)+Sin2(x)+…+Sinn(x).
6. Дано натуральное число N. Сколько цифр в числе N
7..Дано натуральное число N. Вычислить сумму его цифр.
8. Пусть A 0=1, Ak=k*Ak-1+1/k, k=1,2,...Для заданного k получить Ak.
9. Дано натуральное число n и действительное число a. Получить a*(a+1)*(a+2)*…*(a+n-1)/
10. Вычислить 
10. Вычислить 
11. Вычислить 
12. Вычислить 
13. Вычислить 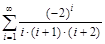
14. Дано натуральное число n. Получить все натуральные числа, меньшие n и взаимно простые с ним.
15. Дано натуральное число n. Получить все простые делители этого числа.
16. Найти натуральное число от 1 до 10000 с максимальной суммой делителей.
17. Даны целые числа P, Q. Получить все делители числа Q взаимно простые с Р.
18. Найти первые 100 простых чисел.
19. Натуральное число называется совершенным, если оно равно сумме всех своих делителей, за исключением себя самого. Число 6 - совершенное, так как 6=1+2+3. Число 8 - не совершенное, так как 8<>1+2+4. Дано натуральное n. Получить все совершенные числа, меньшие n.
20. Напечатать в возрастающем порядке все трехзначные числа, в десятичной записи которых нет одинаковых цифр.
Работа N3. Обработка массивов.
Массивом называется упорядоченная последовательность величин, обозначаемая одним именем. Все элементы массива имеют один и тот же тип. В программе массив должен быть описан либо в разделе описаний переменных, либо в разделе описаний типов. Форма описания имеет вид:
Type
T1 = Array [1..N] of Integer;
T2 = Array [1..5] of Char;
Var
A:T1; {описан массив с именем A}
B:T2; {описан массив с именем B}
C: Array [1..25] of Real; {описан массив с именем C }
Возможно использование многомерных массивов, т.е. массивов. Двумерные массивы еще называют матрицами. Описание многомерных массивов может иметь вид:
Type
T1 = Array [1..N, 1..4] of Integer;
Var
A:T1; {описана матрица с именем A размера N*4}
B: Array [1..5, 1..4] of Real {описана матрица B ра змера 5*4}
Рассмотрим некоторые простейшие алгоритмы обработки массивов:
Ввод-вывод массивов.
Операции ввода-вывода массивов обычно используют циклы. В приведенном ниже примере описан процесс ввода одномерного массива и вывод его в виде столбца.
Program Example1;
Uses Crt;
Const n=5;
Var A: Array [1..n] of Integer;
i: Integer;
Begin
ClrScr;
{Writeln (' Введите элементы массива ');
For i:=1 to n do
Begin
Write('A[',i,']=');
Readln(a[i]);
End;
{Вывод элементов массива}
Writeln(' Массив A');
For i:=1 to n do Writeln(a[i]:5);
Readln;
End.
Поиск минимального в массиве.
Для одномерного массива найти минимальный элемент и определить его номер. Ниже приводится фрагмент программы поиска
Max:=A[1];
IndexMax:=1;
For i:=2 to n do
If Max<A[i] then
begin
Max:=A[i];
IndexMax:=i;
end;
Результат работы содержится в переменных: Max - наибольший элемент массива, IndexMax - номер этого элемента в массиве.
Ниже приводятся задания, целью которых является овладение практическими навыками работы с массивами.
Задания.
1. Даны действительные числа A[1900], A[1901].A[1950] - количество осадков в мм, выпавших в Симферополе в течении первых 50 лет. Надо вычислить среднее количество осадков и отклонение от среднего для каждого года.
2. Даны действительные числа A[1],A[2],A[3],...,A[2*n]. Переставить числа в следующем порядкe A[1],A[n+1],A[2],A[n+2],A[n],A[2*n].
3. Даны действительные числа A[1],A[2],A[3],...,A[2*n]. Переставить числа в следующем порядкe A[1], A[2n], A[2], A[2n-1]...,A[n], A[n+1].
4. Даны действительные числа A[1],A[2],A[3],...,A[2*n]. Получить A[1]+A[2n],A[2]+A[2n-1],...,A[n] + A[n+1].
5. Даны действительные числа A[1],A[2],A[3],...,A[n].Если в результате замены отрицательных членов последовательности их квадратами члены будут организовывать неубывающую последовательность, то получить сумму членов исходной последовательности; в противном случае получить их произведение.
6. Даны действительные числа A[1],A[2],A[3],...,A[n].Получить новую последовательность, выбросив из исходной все члены созначением max(A[1],A[2],A[3],...,A[n]).
7. Даны действительные A[1],A[2],A[3],...,A[n].Все члены последовательности с четными номерами, предшествующие первому по порядку члену со значением Max(A[1],A[2],A[3],...,A[n]) умножить на Max(A[1],A[2],A[3],...,A[n].).
8. Даны целые числа A[1],A[2],A[3],...,A[n], каждое из которых отлично от нуля. Поменять местами наибольший член последовательности и член с номером M.
9. Даны целые числа A[1],A[2],A[3],...,A[n].Если в данной последовательности ни одно четное число не расположено после нечетного, то получить все отрицательные числа последовательности, иначе - все положительные. Порядок следования чисел в обоих случаях заменяется на обратный.
10. Даны целые числа A[1],A[2],A[3],...,A[n]. Наименьший член последовательности заменить целой частью среднего арифметического всех членов последовательности, остальные члены оставить без изменения. Если в последовательности несколькo членов со значением Min(A[1],A[2],A[3],...,A[n]), то заменить последний по порядку.
11. Даны целые числа A[1],A[2],A[3],...,A[n], каждое из которых является либо 0, либо 1, либо 2. Переставить числа так, чтобы сначала шли только 0, затем только 1, затем только 2.
12. Элементы массива Х преобразовать по следующему правилу (воспользоваться массивом У, как вспомогательным): все отрицательные элементы массива Х перенести в его начало, а все остальные - в конец, сохраняя исходное взаимное расположение как среди отрицательных, так и среди всех остальных элементов.
13. Элементы массива Х преобразовать по следующему правилу (воспользоваться массивом У, как вспомогательным): все элементы массива Х циклически сдвинуть вправо на k позиций.
14. Даны действительные числа A[1],A[2],A[3],...,A[n]. Найти сумму чисел этой последовательности, расположенных между максимальным и минимальным числами (в сумму включить и оба этих числа).
15. Даны две последовательности по 30 чисел в каждой. Найти наименьшее среди тех чисел первой последовательности, которые не входят во вторую последовательность (считая, что хотя бы одно такое число есть).
16. Даны целые числа A[1],A[2],A[3],...,A[n] (в этой последовательности могут быть повторяющиеся члены). Получить все числа последовательности, которые входят в нее по одному разу.
17. Построить пересечение последовательностей A[1],A[2],A[3],...,A[n] В[1],В[2],В[3],...В[n]. Т.е. получить в каком либо порядке числа, принадлежащие одновременно обеим последовательностям.
(Если возникают трудности, попробуйте решить эту задачу, предполагая, что среди членов последовательности А нет повторяющихся и среди членов последовательности В нет повторяющихся)
18. Даны целые числа A[1],A[2],A[3],...,A[n]. Для каждого из этих чисел выяснить сколько раз оно входит в эту последовательность. Результат представить в виде ряда строк, первая из которых есть А[1] - k, где k - есть число вхождений А[1] в последовательность. Вторая строка будет иметь вид А[i] - m, где А[i]- есть первый по порядку член, отличный от А[1], m – число вхождений этого члена в последовательность и т.д.
19. Даны целые числа A[1],A[2],A[3],...,A[n]. Получить новую последовательность, заменяя A[i] нулями, если │A[i]│<>Max(A[1],A[2],A[3],...,A[n]) и заменяя A[i] единицей в противном случае.
20. Даны целые числа A1,A2,... An. Оставить ее без изменения, если она упорядочена по неубыванию или по невозрастанию; в противном случае удалить из последовательности те члены, порядковые номера которых кратны четырем, сохранив прежним порядок оставленных членов.






