7.1. Параллельность плоскостей
Плоскости наз-ся параллельными, если они не имеют общей ________.
Признак: если _______ пересекающиеся прямые одной пл-ти соответ-ственно параллельны __________ пересекающимся прямым другой _____, то эти пл-ти _________________________.
Задача. Дана пл-ть, заданная прямыми __________. Через т. _____ провести __________, параллельную _______________.
1.В данной пл-ти проводим произвольно вспомогательную прямую ___, пересекающуюся с прямыми _____ и _____. Проекции точек пересечения _____ и _____ должны находиться на соответствующих линиях связи.
2.Из заданной т. _____ проводим прямые ____________ и ___________, т.е. на чертеже __________, __________ и __________, __________. Пересекающиеся прямые _____ и _____ однозначно ____________________ искомую _______________.
7.2. Пересекающиеся плоскости общего и частного положений
Две пл-ти пересекаются по прямой, которая задаётся _______ точками.
Линия пересечения ______________ принадлежит _____________ пл-тям.
Если одна из пл-тей – пл-ть ______ положения (на рис. фронтально-_________ S1), то проекция линии пересечения _____ находится на вырожденной проекции пл-ти __________________ положения.
Задача. Даны 2 пересекающиеся пл-ти:
--фронтально-проецирующая пл. ____, заданная на чертеже своей ____________ проекцией _______ (_______________) на фронтальной пл-ти __________________.
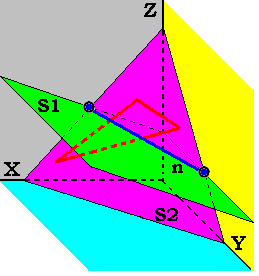--пл-ть общего положения S2, _______ треугольником ____________.
Найти линию пересечения пл-тей __ (т.е. её проекции на чертеже) и _________ этой прямой - т. ______ и т. ______.
1.Линия ______ лежит в пл-ти _____ и совпадает с её следом на ____________ пл-ти проекций. След-но, фронт. проекции точек __________ пересечения линии ___ с ___________ – __________ определены.
2.По линиям связи находятся на гориз. проекции ________________ точки ______, ______ и ч-з них проводится гориз. проекция линии ________.
3.Аналогичным образом строится ____________________________ проекция линии ____________________________________ пл-тей ________.
4.Точки пересечения проекций ______ и ______ с осями X и Z определяют след прямой ______ – точку ______ на фронт. пл. проекций где т. ________; фронт. проекция линии _________ совпадает со следом ________.
5.Точки пересечения проекций ______ и ______ с осями Y и Z определяют след прямой ____ – точку _____ на профильной пл. проекций, где _______.
7.3. Пересечение прямой с плоскостью
Прямая пересекается с _______________ в точке, которая принадлежит этой прямой и ___________________.
Задача. Дана пл. ______, заданная прямыми __________, и прямая ____.
Определить точку ______ пересечения прямой ______ с пл-тью и ______ часть этой линии.
1.Через заданную прямую проводим вспомогательную пл-ть. ________ положения – фронтально-__________________________. Она задаётся своим следом ______ на ________________________ пл-ти.
2.Искомая точка ______ принадлежит пл-ти ______ и пл-ти ________ и находится на линии ______ пересечения этих ____________. Линия ______ проходит ч-з точки ______ и ______.
Проекции точек ______ и ______ определяются на пересечении _______ линий ______ и ______ со следом пл-ти ______. Проекции ______ и ______ опред-ся линиями ________________________.
3.Искомая точка ______ принадлежит линии ______ и одновременно ли-нии ______, следовательно является точкой их _____________________. На фронтальной пл-ти проекций обе эти линии (______и ______) совпадают со следом ______. Но на горизонтальной пл-ти проекций точка пересечения ли-ний ______ и ______ - т. ______ явно определена. Фронтальная проекция __ определяется __________________ связи на проекции ______.
4. Определяем невидимую часть линии ______ на фронтальной пл-ти проекций, которая будет ____________________ заданной пл-тью ______.
Справа от точки ______ пересечения линии ______ с заданной пл-тью __ проводим произвольную линию связи. На этой линии связи находятся точки ______ и ______. Точка ______ принадлежит линии ______, а точка ______ – заданной пл-ти ______, т.к. лежит на линии ______ пересечения пл-ти _____ со ____________________________________ пл-тью ______.
Для точек ______ и ______ фронтальная пл-ть является пл-тью конкури-рования где их проекции ______ и ______ совпадают. Невидимой будет та точка, горизонтальная проекция которой находится ближе к оси, т.е. т. ___.
Точка ______ принадлежит заданной линии ______. Следовательно, часть линии ______ справа от _____________ пересечения К будет ____________.
7.4. Прямая параллельная плоскости
Ели прямая ________________________ какой-либо прямой, ___________ в пл-ти, то она параллельна и этой __________________.
Задача. Дана пл-ть _________, заданная соответствующими __________. Провести ч-з т. ______ прямую ______, параллельную данной пл-ти.
1.В данной пл-ти проводим произвольную ________________, например, ч-з точки ______ и ______.
2.Ч-з данную т. ______ проводим прямую ______, параллельную вспо-могательной линии ______. Эта прямая ______ будет __________________ параллельно пл-ти ____________.
7.5. Определение истинной длины отрезка прямой на чертеже
Отрезок прямой в пространстве представлен на чертеже ____________ проекциями, которые не отражают истинную длину __________________. Для определения истинной длины отрезка применяют __________________. Суть его заключается в переносе ____________________ в пл-ть. _________ из которой он ______________________________ в натуральную величину.
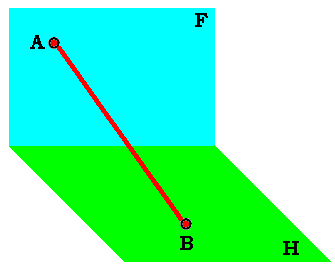Проведём ч-з концы отрезка пл-ти уровня – фронталь ______ ч-з т. _____ и горизонталь _____ ч-з т. ____. На чертеже эти пл-ти представлены своими ________.
Из т.А проведём ____________ ось АО и будем вращать вокруг этой оси __________ (∟АОВ – прямой). Т. ______, скользя, остаётся всегда на пл-ти ______. На чертеже это приведёт к ________________________ проекции _________ вокруг т. ______ и скольжению т. ______ по ________________ пл-ти _____.
Когда _________ совместится с фрон-талью ______, отрезок ________ примет положение _______ и будет проециро-ваться на фронтальную пл-ть проекций (____________) в натуральную величину.
Алгоритм определения истинной дли-ны __________________ отрезка ______:
1. Один из концов отрезка (напр., ______) принимается лежащим на оси вра-щения и ч-з его __________________ (напр., ______, но можно и ______) проводится ______________________________ линия ______.
2. На этой же пл-ти. проекций (на примере – ________________________) проекция второй точки отрезка (______) переносится __________________ на прямую ______ и фиксируется т. ______.
3. На второй пл-ти проекций (на примере – _______________________) ч-з проекцию второй точки ______ данного отрезка проводится _____________ линия ______ и на ней с помощью линии ____________ фиксируется т. ___.
4.На этой пл-ти ______________________ отрезок _________ соответствует истинной ________________________ отрезка _________.
