Основные понятия технического черчения
Учебник: А.М. Хаскин. Черчение.
Задача черчения – представление объёмных объектов на __________ таким образом, чтобы эти объекты можно было воспроизвести в __________ и изготовить.
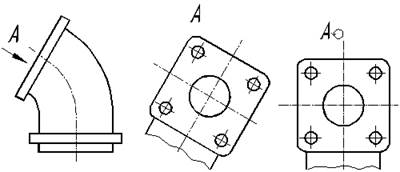Вид– изображение обращенной к наблюдателю видимой части повер-хности предмета. Виды подразделяются на _________________________, ______________________________ и______________________________.
ГОСТ допускает использование 6 основных видов: 1 – главный вид; 2 – вид сверху; 3 – вид слева; 4 – вид справа; 5 – вид сверху; 6 – _________.
Дополнительным наз-ся вид, получаемый на пл-ти, не параллель-ной ни одной из основ-ных _______________ проекций.
Местным видом наз-ся изображение отдельного, ограниченного места поверхности __________.
Совокупность видов наз-ся ____________________.
Чертежи представляются на листах определённого размера (_____________).
Форматы подразделяются на ____________________ и дополнительные. К основным форматам относятся форматы А5,А4,А3, A2,A1 и А0. Меньший формат получается из большего путём деления линией, _______________ короткой стороне.Наиболее распространены форматы _______________.
Дополнительные форматы образуются умножением коротких __________ основных форматов на целое число. Обозначение доп. формата состоит из обозначения _______________ формата и его кратности. Напр.: __________.
На форматном листе чертится рамка, где помещаются основная ________ и дополнительная _______________, содержащая повёрнутый на _________ или 180° код чертежа. Для нас код чертежа имеет структуру:
___________________________________ (год, вариант, задача).
Заполнение основной надписи см. учебник с. 265-268.
Масштаб – это отношение размеров объекта на чертеже к _______ действительным размерам. Они подразделяют на три группы:
натуральная _______________ – _________;
масштабы уменьшения – 1:2; 1:2,5; 1:4; 1: _____; 1:10; 1:15; 1:20 и т. д.
масштабы увеличения – 2:1; 2,5:1; _____ :1; 5:1; 10:1; 20:1; 40:1; 50:1; 100:1.
Напр., масштаб 1:2 означает, что 1мм на чертеже соответствует ________ детали. На чертеже всегда даются реальные размеры детали, _____________ от масштаба.
Линии. Чертежи выполняются разными линиями в _______________ от их назначения: (см. таб.). Линии применяются для:
1. изображения видимо-го контура __________.
2. размерных и вынос-ных линий, __________.
3. линий обрыва длин-ной детали и линий раз-граничения вида и ____
4. линий невидимого контура; пересекаются и заканчиваются _______________.
5.осевых и центровых _________; пересекаются и заканчиваются штрихами;
6. обозначения ____________________ плоскости ____________________.
Шрифты. Надписи на чертеже выполняются чертёжным шрифтом (см. с.18-27). Для нанесения надписи проводятся направляющие _____________, определяющие размер шрифта (_____). Наиболее часто используются шриф-ты 5, 7, 10, 14 и 20. Направляющие определяют высоту ____________ и строчных букв и цифр, а также нижние элементы букв _________.
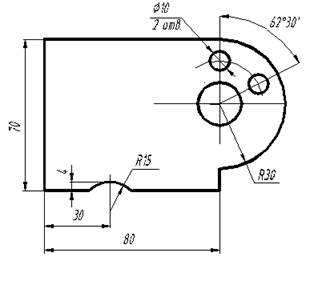
Нанесение размеров. На черте-же должно быть _______________ число размеров, но достаточное для изготовления ______________. Линейные размерынаносят в мил-лиметрах без указания __________
измерения. а угловые – в __________, минутах и секундах с указанием _____.
Размеры, характеризующие _____ наибольших измерения предмета – длину, высоту и _______________, наз-ся габаритными. Размерные _________ предпочтительно наносить вне контура изображения, выносные и __________ линии не должны пересекаться.
Базой наз-ся плоскость, __________ или точка от которой отсчитываются размеры.
Обычно размеры проставляются____________________, координатным или _________________________ способом. Самостоятельно учебник п.4.2 (с.28-37), п.20.5, 20.6 (с.268 - 277).
Разрез - изображение предмета, мысленно рассеченного ____________. На разрезе показывают то, что получается в секущей плоскости и то, что расположено за ней. Положение секущей плоскости указывают на _______ разомкнутой линией. Фирура, полученная в сечении, __________________.
Если секущая пл-ть проходит ч-з ось или пл-ть симметрии _________ __ и параллельна пл-ти чертежа, она не обозначается и сечение _______ _____ на ____________________ детали. Учебник п.18.3 с.208-216.
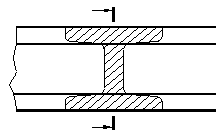Сечение – аналогично разрезу, но показыва-ется только фигура, получаемая в ___________ пл-ти. Сечение является составной __________ разреза. Сечения бывают ___________________ и ____________________.
Вынесенные сечения располагаются _____ изображения предмета; наложенные – ____________________ с изображе-нием детали. Учебник п.18.4 с.217-220.
Выносной элемент – _____________ в более крупном масштабе какой-либо части детали, содержащее __________, не указанные на основном __________.
Задача начертательной геометрии. Методы проецирования.
Задачей нач.геометрии является формирование теоретической _____ технического черчения с целью правильного и однозначного _____________ объекта на _______________.
Проецированием наз-ся получение на плоскости __________________ объекта, освещённого воображаемым источником света. Лучи ___________ наз-ся _________________________ прямыми.
Центральное проецирование – проецирующие прямые _____________ из одной точки (центра ____________________ S). Применяется в архитек-туре при изображении _________________________.
Параллельное проецирование – проецирующие прямые __________ (центр проекций находится в _________________________).
Ортогональное проецирование – частный случай _________________ проецирования, когда проецирующие прямые перпендикулярны __________ проекций. Именно этот метод используется в _______________.
Свойства ортогонального проецирования.
1.Проекцией точки является _______________.
2.Проекцией прямой является прямая (__________) или точка (_______).
3.Если точка С принадлежит прямой _______, то проекция точки _____ принадлежит проекции прямой ________ (или __________ ).
4.Отношение отрезков, лежащих на одной прямой, равно _____________ проекций этих отрезков: ______________________________.
5.Длина проекции _______________ меньше или равна длине самого отрезка _________________________.
6.Если прямые параллельны (____________ и ____________), то их про-екции параллельны (________________) или совпадают (______________).
7.Eсли прямая (_____) перпендикулярна двум пересекающимся _______ пл-ти (_____ и_____), то она будет перпендикулярна этой пл-ти и _______ прямой ей принадлежащей.
8.Если одна сторона прямого угла параллельна пл-ти _______________ (АС||А1С1), а другая к ней не перпендикулярна, то ____________________ угол проецируется на этой пл-ти в натуральную величину.
9. Проекция фигуры не изменяется при параллельном переносе пл-ти ____________________.
Обратимостью чертежа наз-ся его способность однозначно ____________ реальный объект. Задачу создания обратимого чертежа решил французский учёный _________________________. Он предложил ___________________ проецировать объект на минимум _______ взаимно перпендикулярных пл-ти проекций. Для простейших объектов достаточно 2 пл-ти проекций, для реальный деталей используют _____ проекции, для сложных – до _____.
3. Трёхплоскостной чертёж точки.
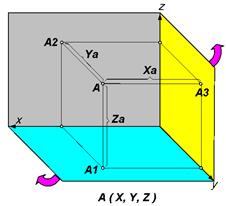
Простейший объект – _____________. В пространстве она характеризуется __________ координатами в системе трёх осей.
Координаты (____________________) определяют расстояние точки до __________ проекций. A1, A2, A3 – проекции точки А на пл-ти проекций: _______________________, ______________________________ и _________________________.
Чертёж – это 2 или 3 проекции точки на эти пл-ти, когда последние _____ повёрнуты до совмещения с _________________________ плоскостью.
Линии связи соединяют проекции точки. Они всегда параллельны ______. Линии связи между _________________________ и профильной __________ проходят через ______________________________. Если:
А(30,25,35) – точка находится в _________________________;
В(0,0,0) – точка лежит в ________________________________________;
С(0,0,20) – точка лежит на __________, в данном случае но оси Z;
D(0,20,30) – точка лежит на __________, в данном случае на профильной;
По двум проекциям точки можно всегда построить третью ____________, используя ___________________________________.
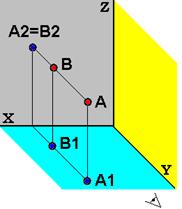Конкурирующими наз-ся две и более _________ (________) лежащих на одной проецирующей пря-мой. Пл-ть проекций, к которой _______________ прямая перпендикулярна, наз-ся пл-тью конкури-рования. На ней проекции конкурирующих точек совпадают (__________). При взгляде на пл-ть кон-курирования видимой будет та точка, __________ которой наиболее удалены от ___________ (т. ___).
4. Чертёж прямой
В пространстве прямая задаётся двумя _______________ или __________ и направлением. Отрезок прямой задаётся двумя _______________.
На чертеже прямая или отрезок задаются _________________________ двух точек этой _________________________.
Прямая общего _________________________ – прямая, наклонённая ко всем пл-тям проекций. Её проекции являются линиями, наклонёнными к осям. Проекции отрезка общего положениявсегда меньше самого ________. Если длины проекций известны, то истинная _______________ отрезка:
АВ = √(А1В1)2 + (А2В2)2 + (А3В3)2;
Прямая уровня - прямая, параллельная какой-либо пл-и ____________.
В параллельную пл-ть проекций отрезок уровня ____________________ в натуральную величину. Проекции прямой уровня в ____________________ пл-ти параллельны осям.
Проецирующая прямая - прямая, перпендикулярная к какой-либо _____ проекций. Проекция прямой на _________________________ пл-ть – точка, на параллельные пл-ти – прямые, параллельные ____________. На парал-лельную пл-ть проекций отрезок _______________________ прямой прое-цируется в _________________________ величину.
Следы прямой.
Следом прямой наз-ся точка пересечения прямой с пл-тью __________. След – это точка на пл-ти проекций и поэтому она обладает следующими свойствами:
-- мин. одна _________________________ = 0, напр., А (___________);
--две проеции точки _____________________________________________.
Задача. Определить __________ прямой, заданной отрезком __________.
При определении ____________________ прямой исходят из того, что эти точки ____________________ одновременно прямой и пл-ти _____________.
Для определения проекций следов ____________________:
1) продолжают проекции отрезка до пересечения с _________________.
Продолжения проекций отрезка _________________________ с осями в точках _____________________________________________.
2) из полученных __________ пересечения проекций прямой с ________ проводят линии связи на смежные пл-ти ____________________;
3) точка пересечения _________ линий связи с проекцией _____________ будет проекцией _________________________ прямой. В точках _______ и __________ пересекаются две линии связи и продолжение _______________.
Следы прямой _____ и _____ заданы ____________________ проекциями.
ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМЫХ
Прямые в пространстве могут располагаться ____________________ друг другу, _________________________ или _________________________.
Прямые параллельны если они ____________________ одной пл-ти и не ______________________________ общей _______________.
Прямые пересекаются если они ____________________ одной ______ и имеют одну _______________точку.
Прямые скрещиваются если они не параллельны и не ______________.
Если прямые параллельны, то их проекции ________________ между собой либо ____________________, либо представляют две _____________.
Определение: если точка лежит на прямой, то проекции точки _______ на проекциях прямой и соединены линиями ______________. Поэтому, если прямые пересекаются, то их проекции __________________________ (или ____________________) и точки пересечения проекций всегда ___________ на одной ____________________ проекционной связи (_______________).
Если прямые скрещиваются, то точки пересечения _________________ не ____________________ на одной ____________________ связи.
ЧЕРТЕЖ ПЛОСКОСТИ
Плоскость задаётся проекциями своего _________________________, под ______________________________ понимают:
--три точки, не лежащие на ______________________________ прямой;
--прямeую и точку ___________________________________;
--две пересекающиеся ___________________________________;
--две _____________________________________________ прямые;
--плоскую _________________________;
--следы ______________________________.
Следы плоскости это ________________ её пересечения с плоскостями проекций. Следы лежат в плоскостях ____________________ и понимаются не как линии, а как заданная _______________.
6.1. Проецирующая плоскость. Это пл-ть, пер-пендикулярная одной из пл-тей проекций. На рис. пл. _____ перпендикулярна гориз-ой пл-ти проекций. Её следы: _____________________. Углы наклона: ____________________.
Проекция пл-ти на ____________________ пл-ть. проекций а1 есть прямая (наз-ся вырож-денная проекция пл-ти), наклоненная к _______. На чертеже проецирующие пл-ти ____________ своими вырожденными проекциями.
Проекция фигуры, находящейся в _________________________ пл-ти, на перпендикулярную пл-ть проекций есть _______________, расположен-ная на вырожденной проекции _________________________ пл-ти.
В зависимости от _________ проекций, к которой перпендикулярна проецирующая пл-ть, последняя наз-ся: _________________________-про-ецирующая, фронтально-проецирующая или ________________-проец-щая.
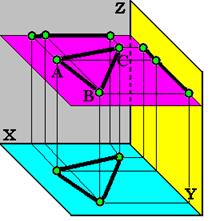6.2.Плоскость уровня.
Это пл-ть, _______________________ какой-либо пл-ти ____________________.
На рис. плоскость, заданая _____________ АВС, параллельна _________________________ пл-ти проекций.
Проекция этой пл-ти на __________________ пл-ти проекций – прямые (__________________ проекции), параллельные осям _________________________.
Фигура в пл-ти уровня _________________________ на параллельную пл-ть __________________ в натуральную величину (___________________).
А2В2С2 и __________ – вырожденные проекции треугольника ________.
Пл. уровня является одновременно _________________________ пл-тью (на примере – фронтально- и _____________________-проецирующей).
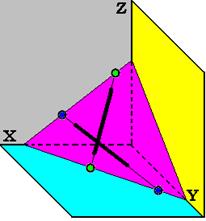6.3. Плоскость общего положения
Это пл., наклоненная к пл-тям _______________.
Фигура в заданной пл-ти ___________________ на пл-ти проекций с _______________________.
На рис. пл. задана двумя ______________ прямыми _____и _____. Следы плоскости могут быть построены по следам __________________ прямых __________ и ___________.
6.4. Принадлежность прямой плоскости. Прямая принадлежит пл-ти:
· если она проходит через _______ точки, принадлежащие ________;
· если она проходит через точку ________ и параллельна __________ прямой, _________________________ в пл-ти.
Для построения прямой, _________________________ пл-ти, её надо провести через _______ точки, принадлежащие __________________ пл-ти.
Задача. Дана пл-ть, заданная двумя пересекающимися прямыми _____ и _____. Отрезок с лежит в этой пл-ти и задан своей фронтальной __________ с2. Определить ______________________________ проекцию отрезка _____.
1.Проводим через отрезок _____ прямую. Поскольку прямые _________ и _____ лежат в одной пл-ти, то они пересекаются, а не ___________________. Поэтому проекции точек пересечения прямых (__________) соединены ли-ниями ____________. Через заданную проекцию отрезка _______ проводим прямую до пересечения с проекциями _____, _____ и находим __________ точек пересечения _______ и _______. Проводим линии _______________ и на горизонтальной плоскости проекций находим проекции точек _______ и _____ на пересечении проекций прямых _____, _____ и соответствующих _________________________ связи.
2.Через точки _______ и _______ проводим прямую – это будет гори-зонтальная проекция прямой _____. На этой проекции прямой ____________ с помощью линий связи горизонтальную проекцию отрезка _____ – ______.
6.4. Принадлежность точки плоскости
Точка принадлежит пл-ти, если она лежит на прямой, принадлежащей ____.
Для построения _____________ на пл-ти надо на данной пл-ти _________ вспомогательную линию и затем на этой линии построить __________.
Задача. Дана пл-ть, заданная тремя точками _____, _____ и _____. Точка _____, лежащая на этой пл-ти, задана своей горизонтальной проекцией ___. Определить ______________________________ проекцию т. _____.
1.Проводим вспомогательную ___________________, на которой должна находиться т. _____. Пусть это будет линия, заданная отрезком _______. Её ____________________________ проекция проходит ч-з т. ______ и ______.
2.Для построения фронтальной проекции отрезка _______ надо ________ ещё один вспомогательный отрезок _______, обе проекции которого ______ и _________ определены. Этот отрезок также находится в заданной _______. Горизонтальная проекция точки пересечения отрезков ________ известна.
3.Фронтальная проекция т. _______ находится на фронтальной ________ отрезка ________ и определяется ____________________ связи из т. _____.
4.Фронтальная проекция вспомогательной _______________ проводится ч-з точки _______ и _______.
5.На вспомогательной линии находится т. _______, искомая фронтальная проекция которой _____ определяется линией связи из т. _______.
