Дифференциальное уравнение первого порядка имеет вид
 (1).
(1).
Решив уравнение (1) относительно  , если это возможно, получим:
, если это возможно, получим:
 (2).
(2).
Общим решением дифференциального уравнения первого порядка называется функция  , содержащая одну произвольную постоянную С и удовлетворяющая условиям:
, содержащая одну произвольную постоянную С и удовлетворяющая условиям:
1. Функция  является решением дифференциального уравнения при каждом фиксированном значении С.
является решением дифференциального уравнения при каждом фиксированном значении С.
2. Каково бы ни было начальное условие  , можно найти такое значение постоянной
, можно найти такое значение постоянной  , что функция
, что функция  удовлетворяет данному начальному условию.
удовлетворяет данному начальному условию.
Частным решением дифференциального уравнения первого порядка называется любая функция  , полученная из общего решения
, полученная из общего решения  при конкретном значении постоянной
при конкретном значении постоянной  .
.
С геометрической точки зрения  есть семейство интегральных кривых плоскости Оху; частное решение
есть семейство интегральных кривых плоскости Оху; частное решение  - одна кривая этого семейства, проходящая через точку
- одна кривая этого семейства, проходящая через точку  .
.
Задача отыскания решения дифференциального уравнения первого порядка, удовлетворяющего заданному начальному условию, называется задачей Коши.
Справедлива следующая теорема о существовании и единственности решения дифференциального уравнения (2).
Теорема (Коши). Если в уравнении  функция
функция  и ее частная производная
и ее частная производная  непрерывны в некоторой области D на плоскости хОу, содержащей точку
непрерывны в некоторой области D на плоскости хОу, содержащей точку  , то существует единственное решение
, то существует единственное решение  этого уравнения, удовлетворяющее условию
этого уравнения, удовлетворяющее условию  .
.
Геометрический смысл этой теоремы состоит в том, что при выполнении ее условий существует единственная интегральная кривая дифференциального уравнения, проходящая через точку  .
.
Дифференциальные уравнения первого порядка с разделяющимися переменными
Определение: Уравнение вида 
называется уравнением с разделяющимися переменными.
Решение:.
Разделив обе части на  , получим:
, получим:
 .
.
Проинтегрировав, обе части уравнения, получим:

 .
.
Пример. Найти общий интеграл уравнения:  .
.
Решение:  ,
,
 ,
,
Разделим обе части уравнения на  , получим:
, получим:
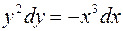 ,
,
проинтегрируем обе части
 ,
,
Ответ:  .
.
 Однородные дифференциальные уравнения
Однородные дифференциальные уравнения
К уравнению с разделяющимися переменными приводятся однородные дифференциальные уравнения первого порядка.
Определение: Функция  называется однородной функцией n-го порядка, если при умножении каждого аргумента на произвольный множитель
называется однородной функцией n-го порядка, если при умножении каждого аргумента на произвольный множитель  вся функция умножится на
вся функция умножится на 
 , т е.
, т е.

Например, функция  есть однородная функция четвертого порядка, поскольку
есть однородная функция четвертого порядка, поскольку

Определение: Дифференциальное уравнение

называется однородным, если функция  есть однородная функция нулевого порядка.
есть однородная функция нулевого порядка.
Это уравнение приводится к виду  , и решается подстановкой
, и решается подстановкой  или
или 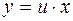 и
и  .
.
Однородное уравнение часто задается в дифференциальной форме
 ,
,
где  и
и  - однородные функции одинакового порядка.
- однородные функции одинакового порядка.
Пример. Найти общий интеграл уравнения
 .
.
Решение: Данное уравнение однородное, т. к. функции  и
и  - однородные функции второго порядка.
- однородные функции второго порядка.
Положим 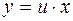 , тогда
, тогда  . Подставляем в исходное уравнение:
. Подставляем в исходное уравнение:
 ,
,
 ,
, 

 ,
,
.
Разделим, и левую, и правую стороны на  , получаем:
, получаем:
 ,
,
отсюда, интегрируя, находим
 ,
,
 ,
,
.
Подставляя  , получим общий интеграл исходного уравнения:
, получим общий интеграл исходного уравнения:
 ,
,
Ответ:.






